Implicit Deep Learning

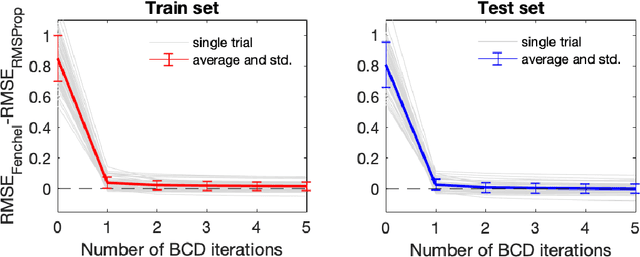
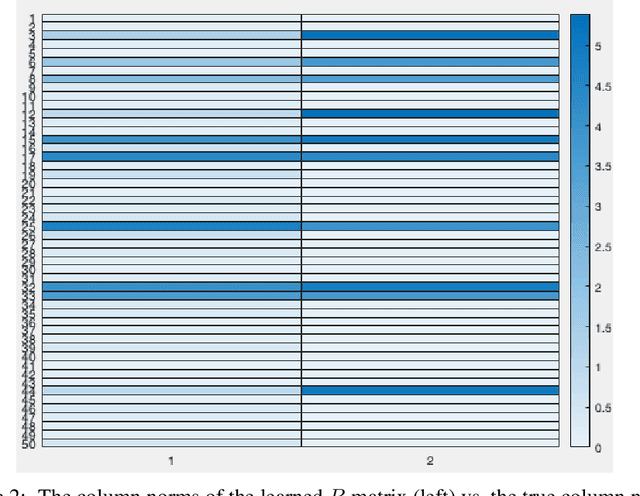
We define a new class of "implicit" deep learning prediction rules that generalize the recursive rules of feedforward neural networks. These models are based on the solution of a fixed-point equation involving a single a vector of hidden features, which is thus only implicitly defined. The new framework greatly simplifies the notation of deep learning, and opens up new possibilities, in terms of novel architectures and algorithms, robustness analysis and design, interpretability, sparsity, and network architecture optimization.

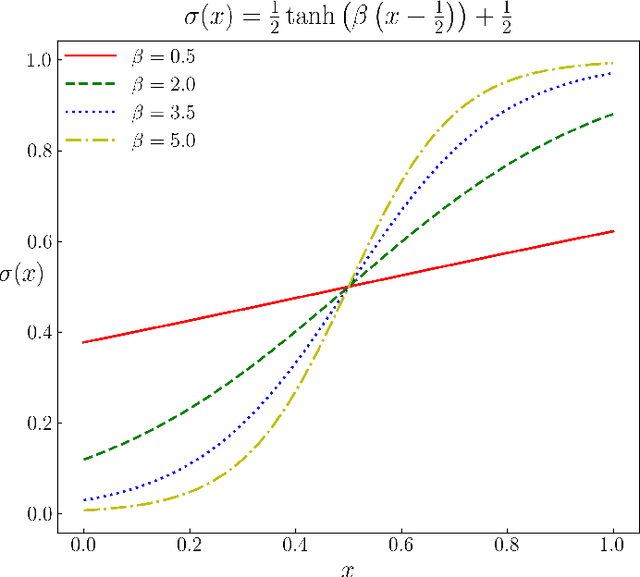
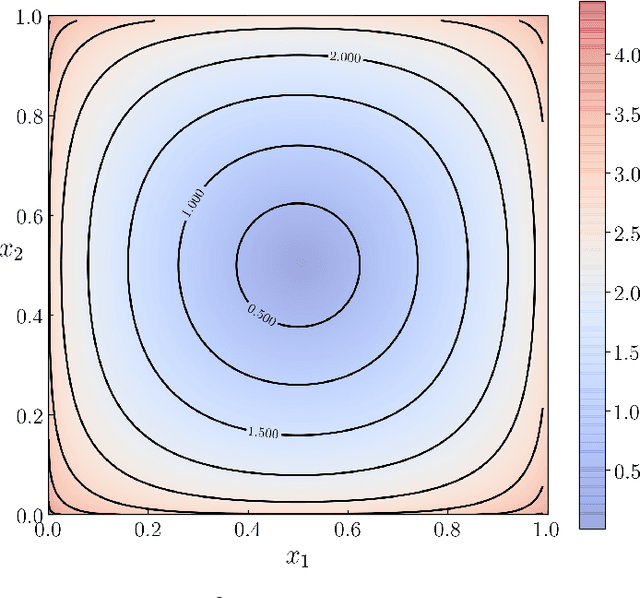
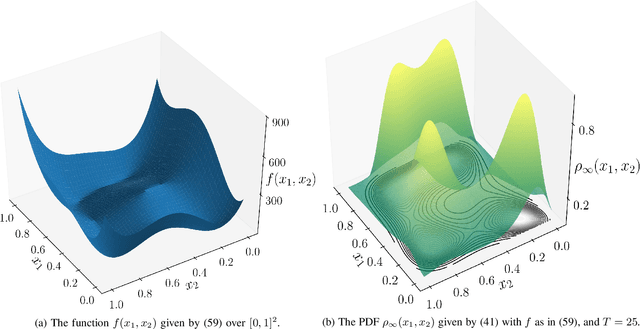
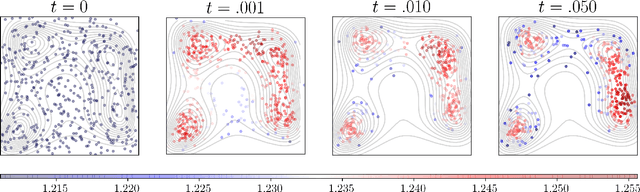
Hopfield Neural Network Flow: A Geometric Viewpoint

We provide gradient flow interpretations for the continuous-time continuous-state Hopfield neural network (HNN). The ordinary and stochastic differential equations associated with the HNN were introduced in the literature as analog optimizers, and were reported to exhibit good performance in numerical experiments. In this work, we point out that the deterministic HNN can be transcribed into Amari's natural gradient descent, and thereby uncover the explicit relation between the underlying Riemannian metric and the activation functions. By exploiting an equivalence between the natural gradient descent and the mirror descent, we show how the choice of activation function governs the geometry of the HNN dynamics. For the stochastic HNN, we show that the so-called ``diffusion machine", while not a gradient flow itself, induces a gradient flow when lifted in the space of probability measures. We characterize this infinite dimensional flow as the gradient descent of certain free energy with respect to a Wasserstein metric that depends on the geodesic distance on the ground manifold. Furthermore, we demonstrate how this gradient flow interpretation can be used for fast computation via recently developed proximal algorithms.