Valuation of Public Bus Electrification with Open Data

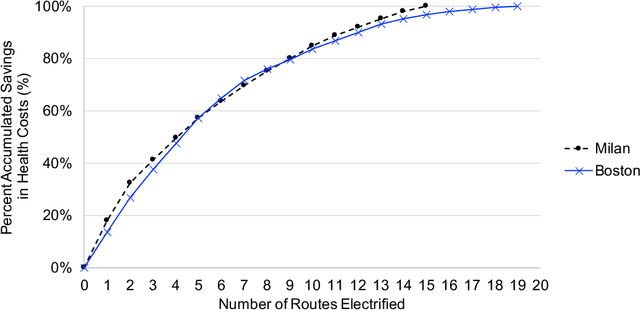
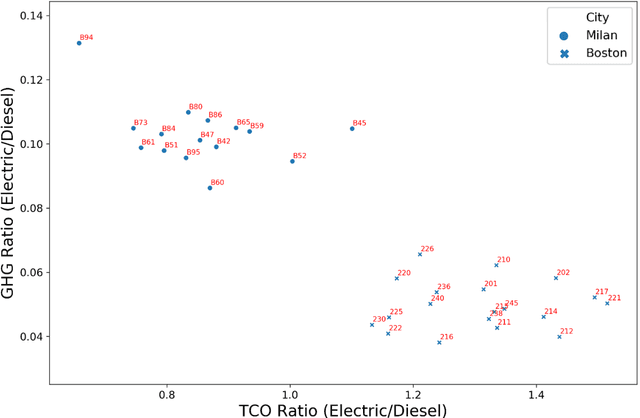
This research provides a novel framework to estimate the economic, environmental, and social values of electrifying public transit buses, for cities across the world, based on open-source data. Electric buses are a compelling candidate to replace diesel buses for the environmental and social benefits. However, the state-of-art models to evaluate the value of bus electrification are limited in applicability because they require granular and bespoke data on bus operation that can be difficult to procure. Our valuation tool uses General Transit Feed Specification, a standard data format used by transit agencies worldwide, to provide high-level guidance on developing a prioritization strategy for electrifying a bus fleet. We develop physics-informed machine learning models to evaluate the energy consumption, the carbon emissions, the health impacts, and the total cost of ownership for each transit route. We demonstrate the scalability of our tool with a case study of the bus lines in the Greater Boston and Milan metropolitan areas.

A Learning-based Optimal Market Bidding Strategy for Price-Maker Energy Storage

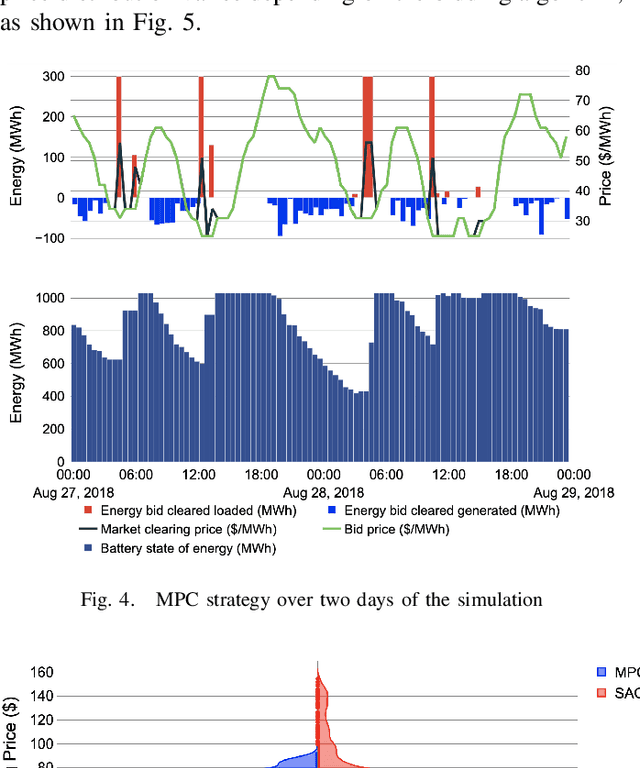
Load serving entities with storage units reach sizes and performances that can significantly impact clearing prices in electricity markets. Nevertheless, price endogeneity is rarely considered in storage bidding strategies and modeling the electricity market is a challenging task. Meanwhile, model-free reinforcement learning such as the Actor-Critic are becoming increasingly popular for designing energy system controllers. Yet implementation frequently requires lengthy, data-intense, and unsafe trial-and-error training. To fill these gaps, we implement an online Supervised Actor-Critic (SAC) algorithm, supervised with a model-based controller -- Model Predictive Control (MPC). The energy storage agent is trained with this algorithm to optimally bid while learning and adjusting to its impact on the market clearing prices. We compare the supervised Actor-Critic algorithm with the MPC algorithm as a supervisor, finding that the former reaps higher profits via learning. Our contribution, thus, is an online and safe SAC algorithm that outperforms the current model-based state-of-the-art.

Risk-Aware Lane Selection on Highway with Dynamic Obstacles

This paper proposes a discretionary lane selection algorithm. In particular, highway driving is considered as a targeted scenario, where each lane has a different level of traffic flow. When lane-changing is discretionary, it is advised not to change lanes unless highly beneficial, e.g., reducing travel time significantly or securing higher safety. Evaluating such "benefit" is a challenge, along with multiple surrounding vehicles in dynamic speed and heading with uncertainty. We propose a real-time lane-selection algorithm with careful cost considerations and with modularity in design. The algorithm is a search-based optimization method that evaluates uncertain dynamic positions of other vehicles under a continuous time and space domain. For demonstration, we incorporate a state-of-the-art motion planner framework (Neural Networks integrated Model Predictive Control) under a CARLA simulation environment.

Safe Wasserstein Constrained Deep Q-Learning

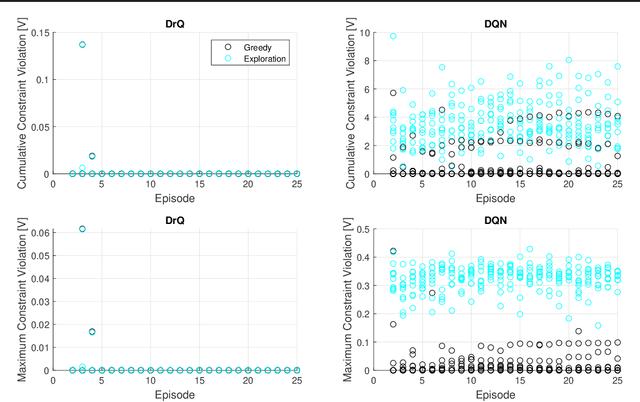
This paper presents a distributionally robust Q-Learning algorithm (DrQ) which leverages Wasserstein ambiguity sets to provide probabilistic out-of-sample safety guarantees during online learning. First, we follow past work by separating the constraint functions from the principal objective to create a hierarchy of machines within the constrained Markov decision process (CMDP). DrQ works within this framework by augmenting constraint costs with tightening offset variables obtained through Wasserstein distributionally robust optimization (DRO). These offset variables correspond to worst-case distributions of modeling error characterized by the TD-errors of the constraint Q-functions. This overall procedure allows us to safely approach the nominal constraint boundaries with strong probabilistic out-of-sample safety guarantees. Using a case study of safe lithium-ion battery fast charging, we demonstrate dramatic improvements in safety and performance relative to a conventional DQN.

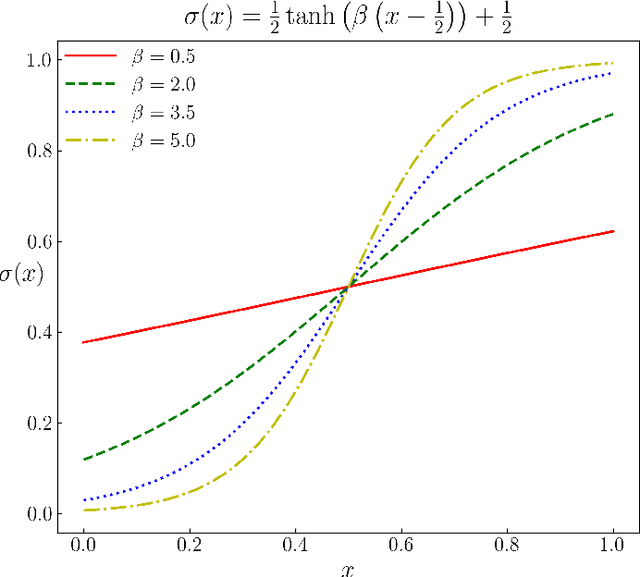
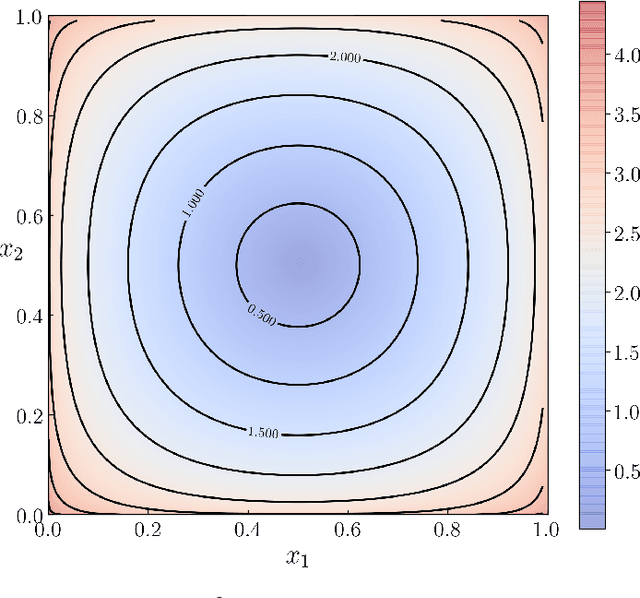
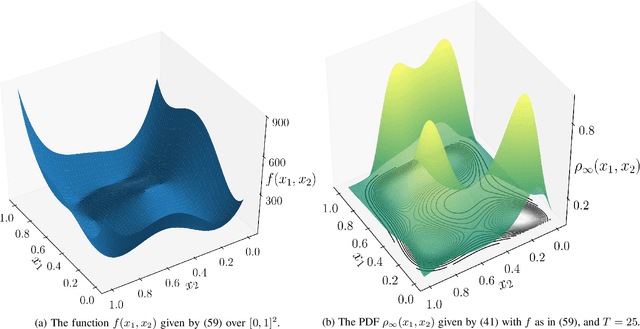
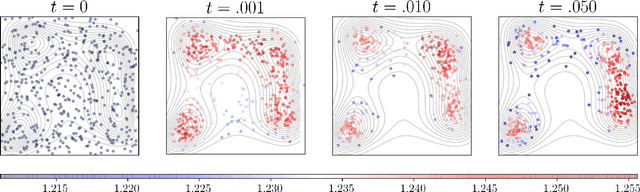
Hopfield Neural Network Flow: A Geometric Viewpoint

We provide gradient flow interpretations for the continuous-time continuous-state Hopfield neural network (HNN). The ordinary and stochastic differential equations associated with the HNN were introduced in the literature as analog optimizers, and were reported to exhibit good performance in numerical experiments. In this work, we point out that the deterministic HNN can be transcribed into Amari's natural gradient descent, and thereby uncover the explicit relation between the underlying Riemannian metric and the activation functions. By exploiting an equivalence between the natural gradient descent and the mirror descent, we show how the choice of activation function governs the geometry of the HNN dynamics. For the stochastic HNN, we show that the so-called ``diffusion machine", while not a gradient flow itself, induces a gradient flow when lifted in the space of probability measures. We characterize this infinite dimensional flow as the gradient descent of certain free energy with respect to a Wasserstein metric that depends on the geodesic distance on the ground manifold. Furthermore, we demonstrate how this gradient flow interpretation can be used for fast computation via recently developed proximal algorithms.