Global Convergence of Second-order Dynamics in Two-layer Neural Networks

Recent results have shown that for two-layer fully connected neural networks, gradient flow converges to a global optimum in the infinite width limit, by making a connection between the mean field dynamics and the Wasserstein gradient flow. These results were derived for first-order gradient flow, and a natural question is whether second-order dynamics, i.e., dynamics with momentum, exhibit a similar guarantee. We show that the answer is positive for the heavy ball method. In this case, the resulting integro-PDE is a nonlinear kinetic Fokker Planck equation, and unlike the first-order case, it has no apparent connection with the Wasserstein gradient flow. Instead, we study the variations of a Lyapunov functional along the solution trajectories to characterize the stationary points and to prove convergence. While our results are asymptotic in the mean field limit, numerical simulations indicate that global convergence may already occur for reasonably small networks.

Reflected Schrödinger Bridge: Density Control with Path Constraints

How to steer a given joint state probability density function to another over finite horizon subject to a controlled stochastic dynamics with hard state (sample path) constraints? In applications, state constraints may encode safety requirements such as obstacle avoidance. In this paper, we perform the feedback synthesis for minimum control effort density steering (a.k.a. Schr\"{o}dinger bridge) problem subject to state constraints. We extend the theory of Schr\"{o}dinger bridges to account the reflecting boundary conditions for the sample paths, and provide a computational framework building on our previous work on proximal recursions, to solve the same.

Gradient Flow Algorithms for Density Propagation in Stochastic Systems

We develop a new computational framework to solve the partial differential equations (PDEs) governing the flow of the joint probability density functions (PDFs) in continuous-time stochastic nonlinear systems. The need for computing the transient joint PDFs subject to prior dynamics arises in uncertainty propagation, nonlinear filtering and stochastic control. Our methodology breaks away from the traditional approach of spatial discretization or function approximation -- both of which, in general, suffer from the "curse-of-dimensionality". In the proposed framework, we discretize time but not the state space. We solve infinite dimensional proximal recursions in the manifold of joint PDFs, which in the small time-step limit, is theoretically equivalent to solving the underlying transport PDEs. The resulting computation has the geometric interpretation of gradient flow of certain free energy functional with respect to the Wasserstein metric arising from the theory of optimal mass transport. We show that dualization along with an entropic regularization, leads to a cone-preserving fixed point recursion that is proved to be contractive in Thompson metric. A block co-ordinate iteration scheme is proposed to solve the resulting nonlinear recursions with guaranteed convergence. This approach enables remarkably fast computation for non-parametric transient joint PDF propagation. Numerical examples and various extensions are provided to illustrate the scope and efficacy of the proposed approach.

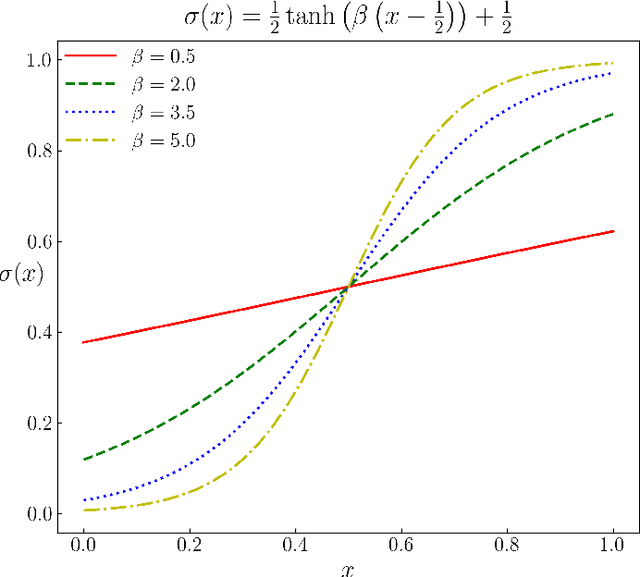
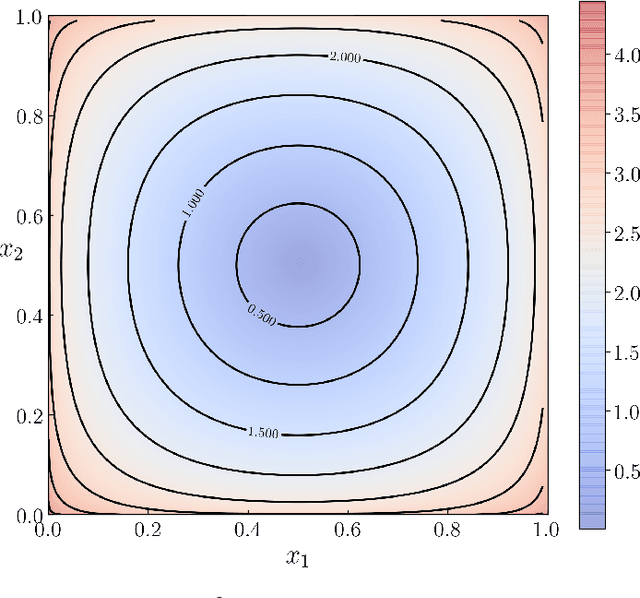
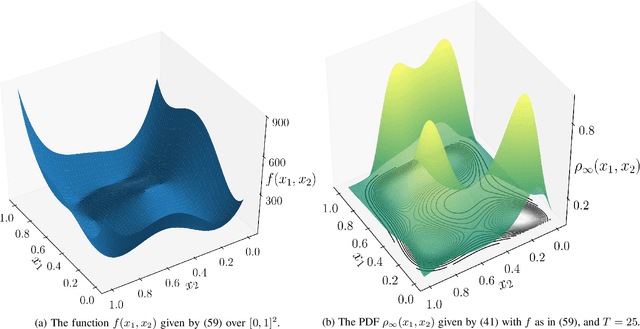
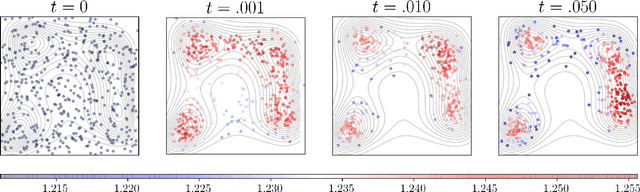
Hopfield Neural Network Flow: A Geometric Viewpoint

We provide gradient flow interpretations for the continuous-time continuous-state Hopfield neural network (HNN). The ordinary and stochastic differential equations associated with the HNN were introduced in the literature as analog optimizers, and were reported to exhibit good performance in numerical experiments. In this work, we point out that the deterministic HNN can be transcribed into Amari's natural gradient descent, and thereby uncover the explicit relation between the underlying Riemannian metric and the activation functions. By exploiting an equivalence between the natural gradient descent and the mirror descent, we show how the choice of activation function governs the geometry of the HNN dynamics. For the stochastic HNN, we show that the so-called ``diffusion machine", while not a gradient flow itself, induces a gradient flow when lifted in the space of probability measures. We characterize this infinite dimensional flow as the gradient descent of certain free energy with respect to a Wasserstein metric that depends on the geodesic distance on the ground manifold. Furthermore, we demonstrate how this gradient flow interpretation can be used for fast computation via recently developed proximal algorithms.