Frank-Wolfe Algorithm for Exemplar Selection

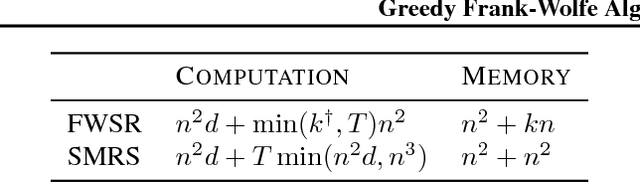
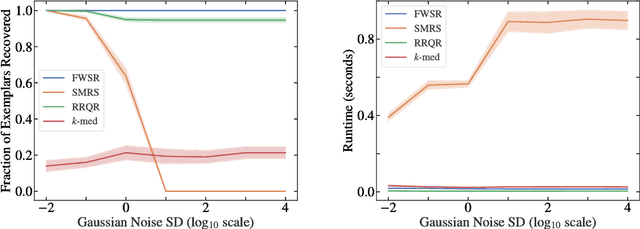
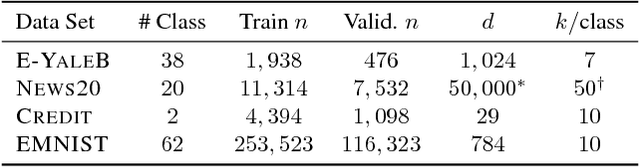
In this paper, we consider the problem of selecting representatives from a data set for arbitrary supervised/unsupervised learning tasks. We identify a subset $S$ of a data set $A$ such that 1) the size of $S$ is much smaller than $A$ and 2) $S$ efficiently describes the entire data set, in a way formalized via auto-regression. The set $S$, also known as the exemplars of the data set $A$, is constructed by solving a convex auto-regressive version of dictionary learning where the dictionary and measurements are given by the data matrix. We show that in order to generate $|S| = k$ exemplars, our algorithm, Frank-Wolfe Sparse Representation (FWSR), only requires $\approx k$ iterations with a per-iteration cost that is quadratic in the size of $A$, an order of magnitude faster than state of the art methods. We test our algorithm against current methods on 4 different data sets and are able to outperform other exemplar finding methods in almost all scenarios. We also test our algorithm qualitatively by selecting exemplars from a corpus of Donald Trump and Hillary Clinton's twitter posts.