Energy Efficient Aerial RIS: Phase Shift Optimization and Trajectory Design

Reconfigurable Intelligent Surface (RIS) technology has gained significant attention due to its ability to enhance the performance of wireless communication systems. The main advantage of RIS is that it can be strategically placed in the environment to control wireless signals, enabling improvements in coverage, capacity, and energy efficiency. In this paper, we investigate a scenario in which a drone, equipped with a RIS, travels from an initial point to a target destination. In this scenario, the aerial RIS (ARIS) is deployed to establish a direct link between the base station and obstructed users. Our objective is to maximize the energy efficiency of the ARIS while taking into account its dynamic model including its velocity and acceleration along with the phase shift of the RIS. To this end, we formulate the energy efficiency problem under the constraints of the dynamic model of the drone. The studied problem is challenging to solve. To address this, we proceed as follows. First, we introduce an efficient solution that involves decoupling the phase shift optimization and the trajectory design. Specifically, the closed-form expression of the phase-shift is obtained using a convex approximation, which is subsequently integrated into the trajectory design problem. We then employ tools inspired by economic model predictive control (EMPC) to solve the resulting trajectory optimization. Our simulation results show a significant improvement in energy efficiency against the scenario where the dynamic model of the UAV is ignored.

Scenario Convex Programs for Dexterous Manipulation under Modeling Uncertainties

This paper proposes a new framework to design a controller for the dexterous manipulation of an object by a multi-fingered hand. To achieve a robust manipulation and wide range of operations, the uncertainties on the location of the contact point and multiple operating points are taken into account in the control design by sampling the state space. The proposed control strategy is based on a robust pole placement using LMIs. Moreover, to handle uncertainties and different operating points, we recast our problem as a robust convex program (RCP). We then consider the original RCP as a scenario convex program (SCP) and solve the SCP by sampling the uncertain grasp map parameter and operating points in the state space. For a required probabilistic level of confidence, we quantify the feasibility of the SCP solution based on the number of sampling points. The control strategy is tested in simulation in a case study with contact location error and different initial grasps.

How to discretize continuous state-action spaces in Q-learning: A symbolic control approach

Q-learning is widely recognized as an effective approach for synthesizing controllers to achieve specific goals. However, handling challenges posed by continuous state-action spaces remains an ongoing research focus. This paper presents a systematic analysis that highlights a major drawback in space discretization methods. To address this challenge, the paper proposes a symbolic model that represents behavioral relations, such as alternating simulation from abstraction to the controlled system. This relation allows for seamless application of the synthesized controller based on abstraction to the original system. Introducing a novel Q-learning technique for symbolic models, the algorithm yields two Q-tables encoding optimal policies. Theoretical analysis demonstrates that these Q-tables serve as both upper and lower bounds on the Q-values of the original system with continuous spaces. Additionally, the paper explores the correlation between the parameters of the space abstraction and the loss in Q-values. The resulting algorithm facilitates achieving optimality within an arbitrary accuracy, providing control over the trade-off between accuracy and computational complexity. The obtained results provide valuable insights for selecting appropriate learning parameters and refining the controller. The engineering relevance of the proposed Q-learning based symbolic model is illustrated through two case studies.

Symbolic Abstractions From Data: A PAC Learning Approach

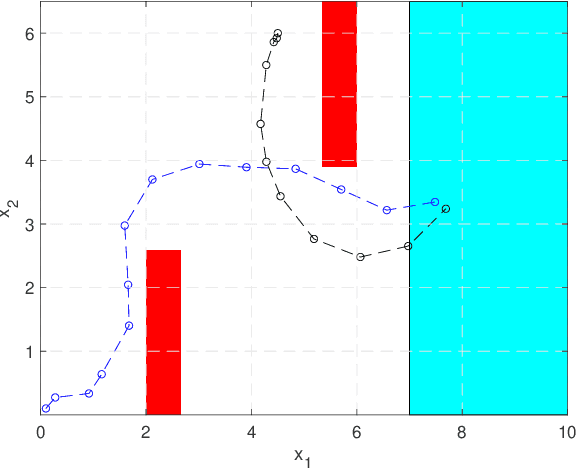
Symbolic control techniques aim to satisfy complex logic specifications. A critical step in these techniques is the construction of a symbolic (discrete) abstraction, a finite-state system whose behaviour mimics that of a given continuous-state system. The methods used to compute symbolic abstractions, however, require knowledge of an accurate closed-form model. To generalize them to systems with unknown dynamics, we present a new data-driven approach that does not require closed-form dynamics, instead relying only the ability to evaluate successors of each state under given inputs. To provide guarantees for the learned abstraction, we use the Probably Approximately Correct (PAC) statistical framework. We first introduce a PAC-style behavioural relationship and an appropriate refinement procedure. We then show how the symbolic abstraction can be constructed to satisfy this new behavioural relationship. Moreover, we provide PAC bounds that dictate the number of data required to guarantee a prescribed level of accuracy and confidence. Finally, we present an illustrative example.