Model-Free $μ$-Synthesis: A Nonsmooth Optimization Perspective
Paper and Code
Feb 18, 2024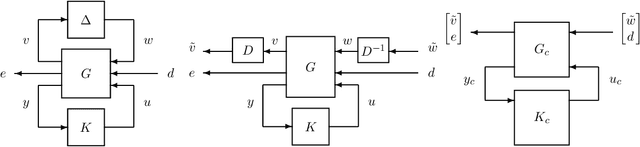

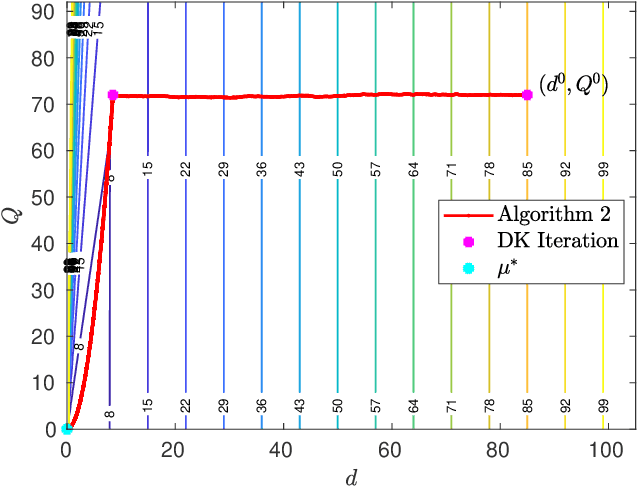
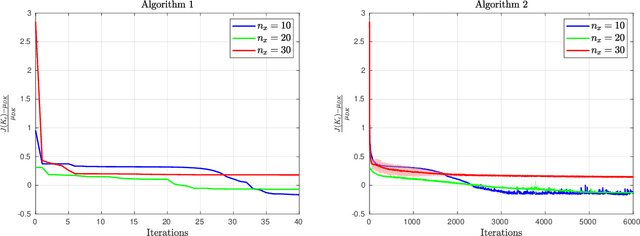
In this paper, we revisit model-free policy search on an important robust control benchmark, namely $\mu$-synthesis. In the general output-feedback setting, there do not exist convex formulations for this problem, and hence global optimality guarantees are not expected. Apkarian (2011) presented a nonconvex nonsmooth policy optimization approach for this problem, and achieved state-of-the-art design results via using subgradient-based policy search algorithms which generate update directions in a model-based manner. Despite the lack of convexity and global optimality guarantees, these subgradient-based policy search methods have led to impressive numerical results in practice. Built upon such a policy optimization persepctive, our paper extends these subgradient-based search methods to a model-free setting. Specifically, we examine the effectiveness of two model-free policy optimization strategies: the model-free non-derivative sampling method and the zeroth-order policy search with uniform smoothing. We performed an extensive numerical study to demonstrate that both methods consistently replicate the design outcomes achieved by their model-based counterparts. Additionally, we provide some theoretical justifications showing that convergence guarantees to stationary points can be established for our model-free $\mu$-synthesis under some assumptions related to the coerciveness of the cost function. Overall, our results demonstrate that derivative-free policy optimization offers a competitive and viable approach for solving general output-feedback $\mu$-synthesis problems in the model-free setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge