DynaMath: A Dynamic Visual Benchmark for Evaluating Mathematical Reasoning Robustness of Vision Language Models

The rapid advancements in Vision-Language Models (VLMs) have shown great potential in tackling mathematical reasoning tasks that involve visual context. Unlike humans who can reliably apply solution steps to similar problems with minor modifications, we found that SOTA VLMs like GPT-4o can consistently fail in these scenarios, revealing limitations in their mathematical reasoning capabilities. In this paper, we investigate the mathematical reasoning robustness in VLMs and evaluate how well these models perform under different variants of the same question, such as changes in visual numerical values or function graphs. While several vision-based math benchmarks have been developed to assess VLMs' problem-solving capabilities, these benchmarks contain only static sets of problems and cannot easily evaluate mathematical reasoning robustness. To fill this gap, we introduce DynaMath, a dynamic visual math benchmark designed for in-depth assessment of VLMs. DynaMath includes 501 high-quality, multi-topic seed questions, each represented as a Python program. Those programs are carefully designed and annotated to enable the automatic generation of a much larger set of concrete questions, including many different types of visual and textual variations. DynaMath allows us to evaluate the generalization ability of VLMs, by assessing their performance under varying input conditions of a seed question. We evaluated 14 SOTA VLMs with 5,010 generated concrete questions. Our results show that the worst-case model accuracy, defined as the percentage of correctly answered seed questions in all 10 variants, is significantly lower than the average-case accuracy. Our analysis emphasizes the need to study the robustness of VLMs' reasoning abilities, and DynaMath provides valuable insights to guide the development of more reliable models for mathematical reasoning.

Benchmarking the Capabilities of Large Language Models in Transportation System Engineering: Accuracy, Consistency, and Reasoning Behaviors

In this paper, we explore the capabilities of state-of-the-art large language models (LLMs) such as GPT-4, GPT-4o, Claude 3.5 Sonnet, Claude 3 Opus, Gemini 1.5 Pro, Llama 3, and Llama 3.1 in solving some selected undergraduate-level transportation engineering problems. We introduce TransportBench, a benchmark dataset that includes a sample of transportation engineering problems on a wide range of subjects in the context of planning, design, management, and control of transportation systems. This dataset is used by human experts to evaluate the capabilities of various commercial and open-sourced LLMs, especially their accuracy, consistency, and reasoning behaviors, in solving transportation engineering problems. Our comprehensive analysis uncovers the unique strengths and limitations of each LLM, e.g. our analysis shows the impressive accuracy and some unexpected inconsistent behaviors of Claude 3.5 Sonnet in solving TransportBench problems. Our study marks a thrilling first step toward harnessing artificial general intelligence for complex transportation challenges.

Capabilities of Large Language Models in Control Engineering: A Benchmark Study on GPT-4, Claude 3 Opus, and Gemini 1.0 Ultra

In this paper, we explore the capabilities of state-of-the-art large language models (LLMs) such as GPT-4, Claude 3 Opus, and Gemini 1.0 Ultra in solving undergraduate-level control problems. Controls provides an interesting case study for LLM reasoning due to its combination of mathematical theory and engineering design. We introduce ControlBench, a benchmark dataset tailored to reflect the breadth, depth, and complexity of classical control design. We use this dataset to study and evaluate the problem-solving abilities of these LLMs in the context of control engineering. We present evaluations conducted by a panel of human experts, providing insights into the accuracy, reasoning, and explanatory prowess of LLMs in control engineering. Our analysis reveals the strengths and limitations of each LLM in the context of classical control, and our results imply that Claude 3 Opus has become the state-of-the-art LLM for solving undergraduate control problems. Our study serves as an initial step towards the broader goal of employing artificial general intelligence in control engineering.

Model-Free $μ$-Synthesis: A Nonsmooth Optimization Perspective

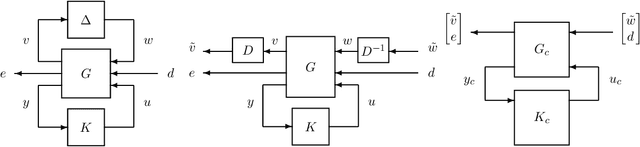
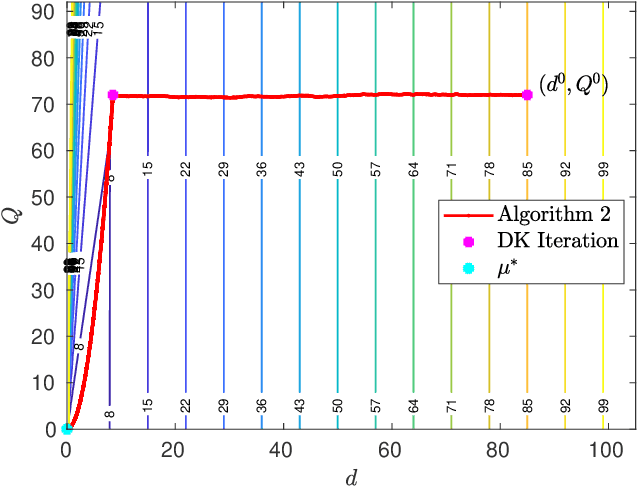
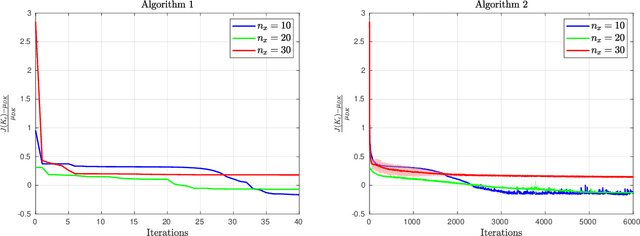
In this paper, we revisit model-free policy search on an important robust control benchmark, namely $\mu$-synthesis. In the general output-feedback setting, there do not exist convex formulations for this problem, and hence global optimality guarantees are not expected. Apkarian (2011) presented a nonconvex nonsmooth policy optimization approach for this problem, and achieved state-of-the-art design results via using subgradient-based policy search algorithms which generate update directions in a model-based manner. Despite the lack of convexity and global optimality guarantees, these subgradient-based policy search methods have led to impressive numerical results in practice. Built upon such a policy optimization persepctive, our paper extends these subgradient-based search methods to a model-free setting. Specifically, we examine the effectiveness of two model-free policy optimization strategies: the model-free non-derivative sampling method and the zeroth-order policy search with uniform smoothing. We performed an extensive numerical study to demonstrate that both methods consistently replicate the design outcomes achieved by their model-based counterparts. Additionally, we provide some theoretical justifications showing that convergence guarantees to stationary points can be established for our model-free $\mu$-synthesis under some assumptions related to the coerciveness of the cost function. Overall, our results demonstrate that derivative-free policy optimization offers a competitive and viable approach for solving general output-feedback $\mu$-synthesis problems in the model-free setting.

COLD-Attack: Jailbreaking LLMs with Stealthiness and Controllability

Jailbreaks on Large language models (LLMs) have recently received increasing attention. For a comprehensive assessment of LLM safety, it is essential to consider jailbreaks with diverse attributes, such as contextual coherence and sentiment/stylistic variations, and hence it is beneficial to study controllable jailbreaking, i.e. how to enforce control on LLM attacks. In this paper, we formally formulate the controllable attack generation problem, and build a novel connection between this problem and controllable text generation, a well-explored topic of natural language processing. Based on this connection, we adapt the Energy-based Constrained Decoding with Langevin Dynamics (COLD), a state-of-the-art, highly efficient algorithm in controllable text generation, and introduce the COLD-Attack framework which unifies and automates the search of adversarial LLM attacks under a variety of control requirements such as fluency, stealthiness, sentiment, and left-right-coherence. The controllability enabled by COLD-Attack leads to diverse new jailbreak scenarios which not only cover the standard setting of generating fluent suffix attacks, but also allow us to address new controllable attack settings such as revising a user query adversarially with minimal paraphrasing, and inserting stealthy attacks in context with left-right-coherence. Our extensive experiments on various LLMs (Llama-2, Mistral, Vicuna, Guanaco, GPT-3.5) show COLD-Attack's broad applicability, strong controllability, high success rate, and attack transferability. Our code is available at https://github.com/Yu-Fangxu/COLD-Attack.

Exact Formulas for Finite-Time Estimation Errors of Decentralized Temporal Difference Learning with Linear Function Approximation

In this paper, we consider the policy evaluation problem in multi-agent reinforcement learning (MARL) and derive exact closed-form formulas for the finite-time mean-squared estimation errors of decentralized temporal difference (TD) learning with linear function approximation. Our analysis hinges upon the fact that the decentralized TD learning method can be viewed as a Markov jump linear system (MJLS). Then standard MJLS theory can be applied to quantify the mean and covariance matrix of the estimation error of the decentralized TD method at every time step. Various implications of our exact formulas on the algorithm performance are also discussed. An interesting finding is that under a necessary and sufficient stability condition, the mean-squared TD estimation error will converge to an exact limit at a specific exponential rate.

Convex Programs and Lyapunov Functions for Reinforcement Learning: A Unified Perspective on the Analysis of Value-Based Methods

Value-based methods play a fundamental role in Markov decision processes (MDPs) and reinforcement learning (RL). In this paper, we present a unified control-theoretic framework for analyzing valued-based methods such as value computation (VC), value iteration (VI), and temporal difference (TD) learning (with linear function approximation). Built upon an intrinsic connection between value-based methods and dynamic systems, we can directly use existing convex testing conditions in control theory to derive various convergence results for the aforementioned value-based methods. These testing conditions are convex programs in form of either linear programming (LP) or semidefinite programming (SDP), and can be solved to construct Lyapunov functions in a straightforward manner. Our analysis reveals some intriguing connections between feedback control systems and RL algorithms. It is our hope that such connections can inspire more work at the intersection of system/control theory and RL.