Vincent Pacelli
Deep Distributed Optimization for Large-Scale Quadratic Programming
Dec 11, 2024
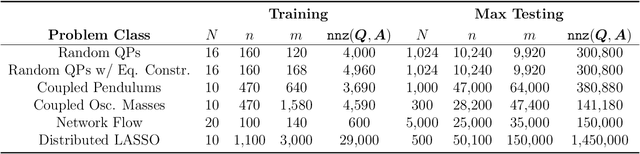


Abstract:Quadratic programming (QP) forms a crucial foundation in optimization, encompassing a broad spectrum of domains and serving as the basis for more advanced algorithms. Consequently, as the scale and complexity of modern applications continue to grow, the development of efficient and reliable QP algorithms is becoming increasingly vital. In this context, this paper introduces a novel deep learning-aided distributed optimization architecture designed for tackling large-scale QP problems. First, we combine the state-of-the-art Operator Splitting QP (OSQP) method with a consensus approach to derive DistributedQP, a new method tailored for network-structured problems, with convergence guarantees to optimality. Subsequently, we unfold this optimizer into a deep learning framework, leading to DeepDistributedQP, which leverages learned policies to accelerate reaching to desired accuracy within a restricted amount of iterations. Our approach is also theoretically grounded through Probably Approximately Correct (PAC)-Bayes theory, providing generalization bounds on the expected optimality gap for unseen problems. The proposed framework, as well as its centralized version DeepQP, significantly outperform their standard optimization counterparts on a variety of tasks such as randomly generated problems, optimal control, linear regression, transportation networks and others. Notably, DeepDistributedQP demonstrates strong generalization by training on small problems and scaling to solve much larger ones (up to 50K variables and 150K constraints) using the same policy. Moreover, it achieves orders-of-magnitude improvements in wall-clock time compared to OSQP. The certifiable performance guarantees of our approach are also demonstrated, ensuring higher-quality solutions over traditional optimizers.
Operator Splitting Covariance Steering for Safe Stochastic Nonlinear Control
Nov 18, 2024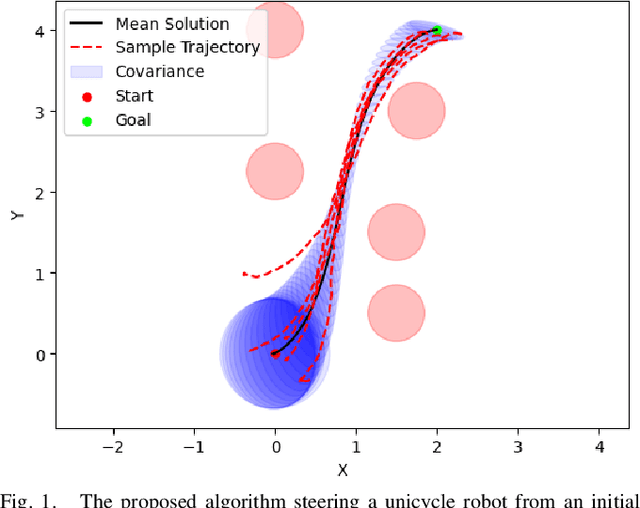
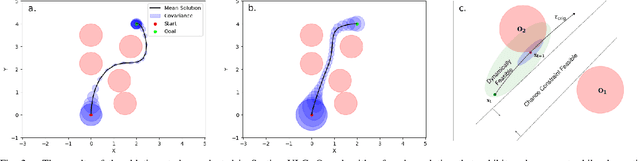

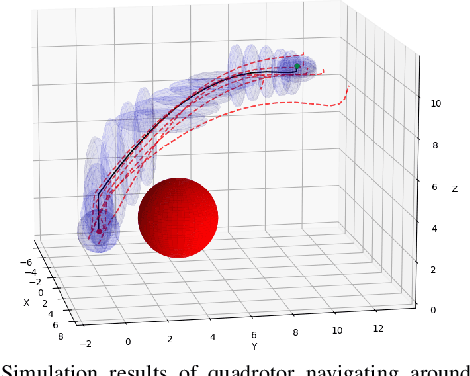
Abstract:Most robotics applications are typically accompanied with safety restrictions that need to be satisfied with a high degree of confidence even in environments under uncertainty. Controlling the state distribution of a system and enforcing such specifications as distribution constraints is a promising approach for meeting such requirements. In this direction, covariance steering (CS) is an increasingly popular stochastic optimal control (SOC) framework for designing safe controllers via explicit constraints on the system covariance. Nevertheless, a major challenge in applying CS methods to systems with the nonlinear dynamics and chance constraints common in robotics is that the approximations needed are conservative and highly sensitive to the point of approximation. This can cause sequential convex programming methods to converge to poor local minima or incorrectly report problems as infeasible due to shifting constraints. This paper presents a novel algorithm for solving chance-constrained nonlinear CS problems that directly addresses this challenge. Specifically, we propose an operator-splitting approach that temporarily separates the main problem into subproblems that can be solved in parallel. The benefit of this relaxation lies in the fact that it does not require all iterates to satisfy all constraints simultaneously prior to convergence, thus enhancing the exploration capabilities of the algorithm for finding better solutions. Simulation results verify the ability of the proposed method to find higher quality solutions under stricter safety constraints than standard methods on a variety of robotic systems. Finally, the applicability of the algorithm on real systems is confirmed through hardware demonstrations.
Feedback Schrödinger Bridge Matching
Oct 24, 2024Abstract:Recent advancements in diffusion bridges for distribution transport problems have heavily relied on matching frameworks, yet existing methods often face a trade-off between scalability and access to optimal pairings during training. Fully unsupervised methods make minimal assumptions but incur high computational costs, limiting their practicality. On the other hand, imposing full supervision of the matching process with optimal pairings improves scalability, however, it can be infeasible in many applications. To strike a balance between scalability and minimal supervision, we introduce Feedback Schr\"odinger Bridge Matching (FSBM), a novel semi-supervised matching framework that incorporates a small portion (less than 8% of the entire dataset) of pre-aligned pairs as state feedback to guide the transport map of non coupled samples, thereby significantly improving efficiency. This is achieved by formulating a static Entropic Optimal Transport (EOT) problem with an additional term capturing the semi-supervised guidance. The generalized EOT objective is then recast into a dynamic formulation to leverage the scalability of matching frameworks. Extensive experiments demonstrate that FSBM accelerates training and enhances generalization by leveraging coupled pairs guidance, opening new avenues for training matching frameworks with partially aligned datasets.
Fundamental Performance Limits for Sensor-Based Robot Control and Policy Learning
Jan 31, 2022



Abstract:Our goal is to develop theory and algorithms for establishing fundamental limits on performance for a given task imposed by a robot's sensors. In order to achieve this, we define a quantity that captures the amount of task-relevant information provided by a sensor. Using a novel version of the generalized Fano inequality from information theory, we demonstrate that this quantity provides an upper bound on the highest achievable expected reward for one-step decision making tasks. We then extend this bound to multi-step problems via a dynamic programming approach. We present algorithms for numerically computing the resulting bounds, and demonstrate our approach on three examples: (i) the lava problem from the literature on partially observable Markov decision processes, (ii) an example with continuous state and observation spaces corresponding to a robot catching a freely-falling object, and (iii) obstacle avoidance using a depth sensor with non-Gaussian noise. We demonstrate the ability of our approach to establish strong limits on achievable performance for these problems by comparing our upper bounds with achievable lower bounds (computed by synthesizing or learning concrete control policies).
Robust Control Under Uncertainty via Bounded Rationality and Differential Privacy
Sep 17, 2021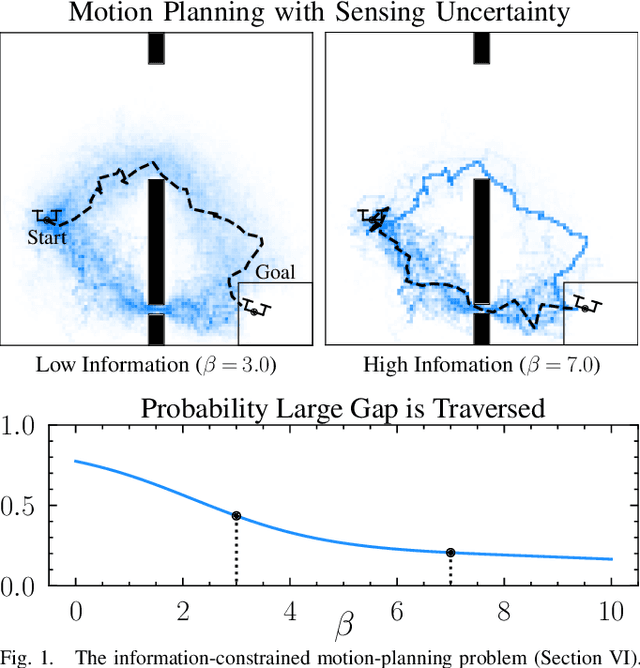
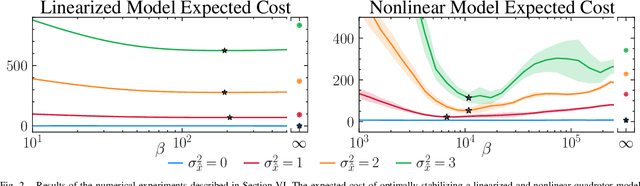
Abstract:The rapid development of affordable and compact high-fidelity sensors (e.g., cameras and LIDAR) allows robots to construct detailed estimates of their states and environments. However, the availability of such rich sensor information introduces two technical challenges: (i) the lack of analytic sensing models, which makes it difficult to design controllers that are robust to sensor failures, and (ii) the computational expense of processing the high-dimensional sensor information in real time. This paper addresses these challenges using the theory of differential privacy, which allows us to (i) design controllers with bounded sensitivity to errors in state estimates, and (ii) bound the amount of state information used for control (i.e., to impose bounded rationality). The resulting framework approximates the separation principle and allows us to derive an upper-bound on the cost incurred with a faulty state estimator in terms of three quantities: the cost incurred using a perfect state estimator, the magnitude of state estimation errors, and the level of differential privacy. We demonstrate the efficacy of our framework numerically on different robotics problems, including nonlinear system stabilization and motion planning.
Invariant Policy Optimization: Towards Stronger Generalization in Reinforcement Learning
Jun 01, 2020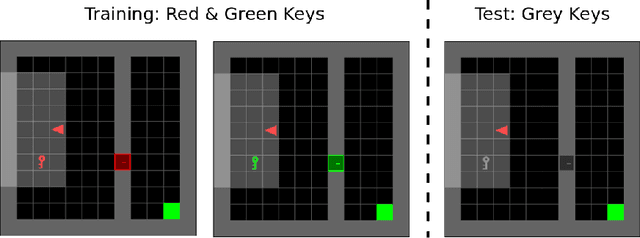

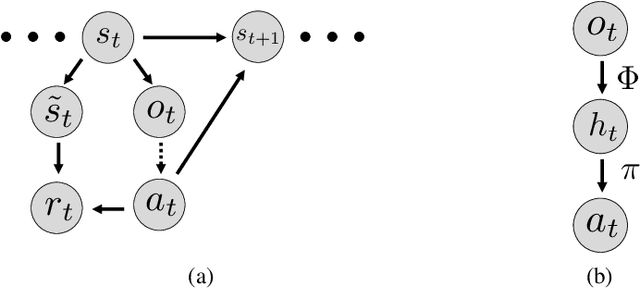

Abstract:A fundamental challenge in reinforcement learning is to learn policies that generalize beyond the operating domain experienced during training. In this paper, we approach this challenge through the following invariance principle: an agent must find a representation such that there exists an action-predictor built on top of this representation that is simultaneously optimal across all training domains. Intuitively, the resulting invariant policy enhances generalization by finding causes of successful actions. We propose a novel learning algorithm, Invariant Policy Optimization (IPO), that explicitly enforces this principle and learns an invariant policy during training. We compare our approach with standard policy gradient methods and demonstrate significant improvements in generalization performance on unseen domains for Linear Quadratic Regulator (LQR) problems and our own benchmark in the MiniGrid Gym environment.
Learning Task-Driven Control Policies via Information Bottlenecks
Feb 04, 2020



Abstract:This paper presents a reinforcement learning approach to synthesizing task-driven control policies for robotic systems equipped with rich sensory modalities (e.g., vision or depth). Standard reinforcement learning algorithms typically produce policies that tightly couple control actions to the entirety of the system's state and rich sensor observations. As a consequence, the resulting policies can often be sensitive to changes in task-irrelevant portions of the state or observations (e.g., changing background colors). In contrast, the approach we present here learns to create a task-driven representation that is used to compute control actions. Formally, this is achieved by deriving a policy gradient-style algorithm that creates an information bottleneck between the states and the task-driven representation; this constrains actions to only depend on task-relevant information. We demonstrate our approach in a thorough set of simulation results on multiple examples including a grasping task that utilizes depth images and a ball-catching task that utilizes RGB images. Comparisons with a standard policy gradient approach demonstrate that the task-driven policies produced by our algorithm are often significantly more robust to sensor noise and task-irrelevant changes in the environment.
Task-Driven Estimation and Control via Information Bottlenecks
Sep 27, 2018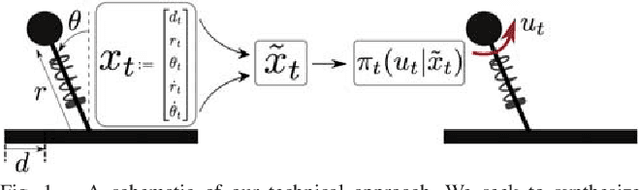
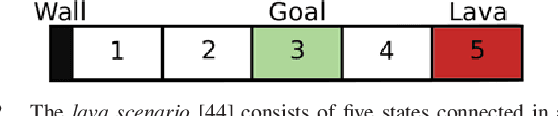
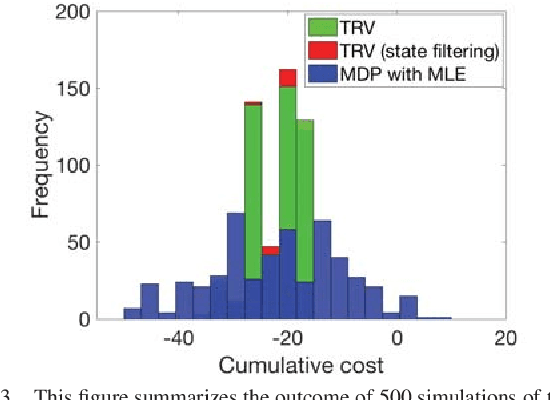
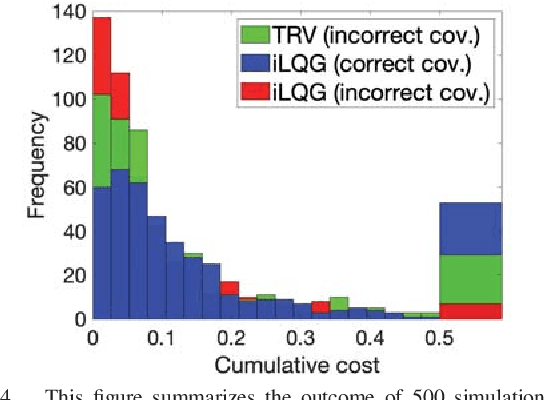
Abstract:Our goal is to develop a principled and general algorithmic framework for task-driven estimation and control for robotic systems. State-of-the-art approaches for controlling robotic systems typically rely heavily on accurately estimating the full state of the robot (e.g., a running robot might estimate joint angles and velocities, torso state, and position relative to a goal). However, full state representations are often excessively rich for the specific task at hand and can lead to significant computational inefficiency and brittleness to errors in state estimation. In contrast, we present an approach that eschews such rich representations and seeks to create task-driven representations. The key technical insight is to leverage the theory of information bottlenecks}to formalize the notion of a "task-driven representation" in terms of information theoretic quantities that measure the minimality of a representation. We propose novel iterative algorithms for automatically synthesizing (offline) a task-driven representation (given in terms of a set of task-relevant variables (TRVs)) and a performant control policy that is a function of the TRVs. We present online algorithms for estimating the TRVs in order to apply the control policy. We demonstrate that our approach results in significant robustness to unmodeled measurement uncertainty both theoretically and via thorough simulation experiments including a spring-loaded inverted pendulum running to a goal location.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge