Robust Control Under Uncertainty via Bounded Rationality and Differential Privacy
Paper and Code
Sep 17, 2021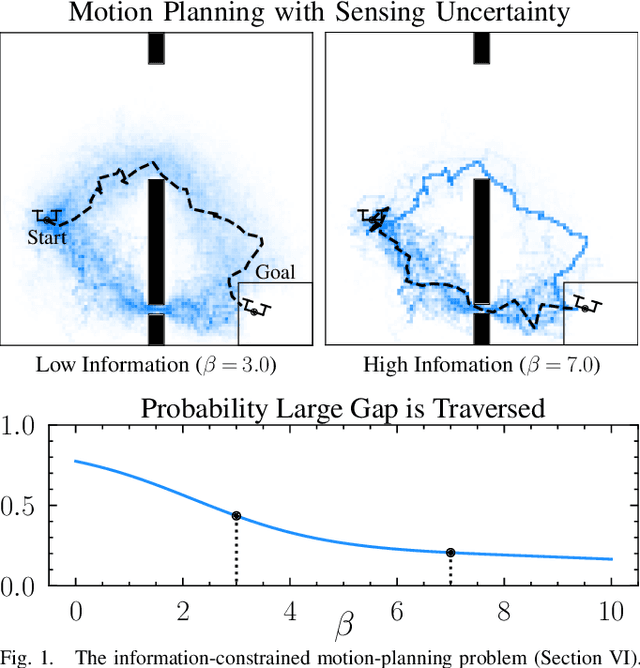
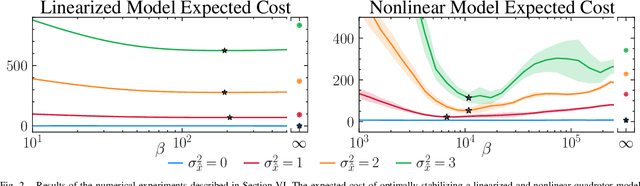
The rapid development of affordable and compact high-fidelity sensors (e.g., cameras and LIDAR) allows robots to construct detailed estimates of their states and environments. However, the availability of such rich sensor information introduces two technical challenges: (i) the lack of analytic sensing models, which makes it difficult to design controllers that are robust to sensor failures, and (ii) the computational expense of processing the high-dimensional sensor information in real time. This paper addresses these challenges using the theory of differential privacy, which allows us to (i) design controllers with bounded sensitivity to errors in state estimates, and (ii) bound the amount of state information used for control (i.e., to impose bounded rationality). The resulting framework approximates the separation principle and allows us to derive an upper-bound on the cost incurred with a faulty state estimator in terms of three quantities: the cost incurred using a perfect state estimator, the magnitude of state estimation errors, and the level of differential privacy. We demonstrate the efficacy of our framework numerically on different robotics problems, including nonlinear system stabilization and motion planning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge