Operator Splitting Covariance Steering for Safe Stochastic Nonlinear Control
Paper and Code
Nov 18, 2024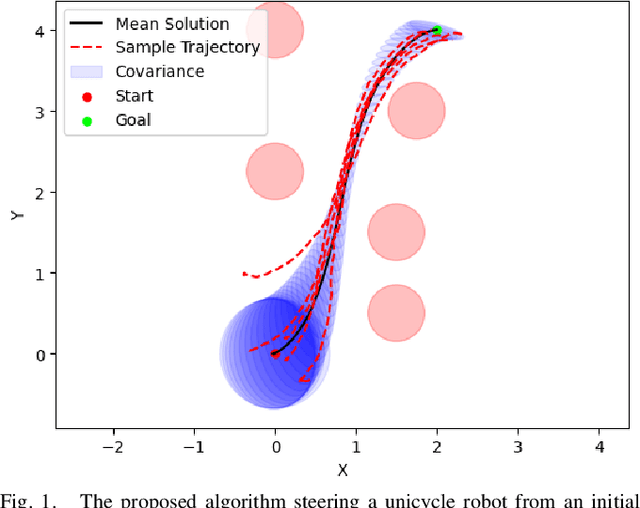
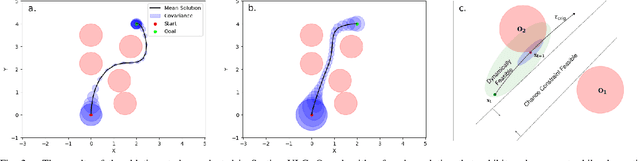

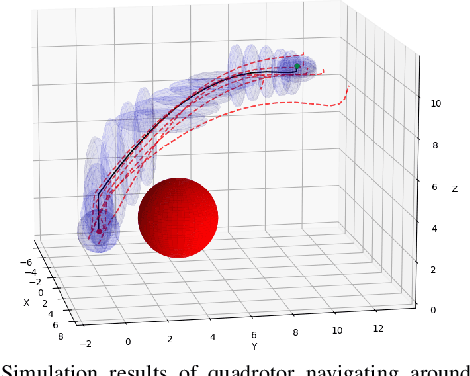
Most robotics applications are typically accompanied with safety restrictions that need to be satisfied with a high degree of confidence even in environments under uncertainty. Controlling the state distribution of a system and enforcing such specifications as distribution constraints is a promising approach for meeting such requirements. In this direction, covariance steering (CS) is an increasingly popular stochastic optimal control (SOC) framework for designing safe controllers via explicit constraints on the system covariance. Nevertheless, a major challenge in applying CS methods to systems with the nonlinear dynamics and chance constraints common in robotics is that the approximations needed are conservative and highly sensitive to the point of approximation. This can cause sequential convex programming methods to converge to poor local minima or incorrectly report problems as infeasible due to shifting constraints. This paper presents a novel algorithm for solving chance-constrained nonlinear CS problems that directly addresses this challenge. Specifically, we propose an operator-splitting approach that temporarily separates the main problem into subproblems that can be solved in parallel. The benefit of this relaxation lies in the fact that it does not require all iterates to satisfy all constraints simultaneously prior to convergence, thus enhancing the exploration capabilities of the algorithm for finding better solutions. Simulation results verify the ability of the proposed method to find higher quality solutions under stricter safety constraints than standard methods on a variety of robotic systems. Finally, the applicability of the algorithm on real systems is confirmed through hardware demonstrations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge