Deep Distributed Optimization for Large-Scale Quadratic Programming

Quadratic programming (QP) forms a crucial foundation in optimization, encompassing a broad spectrum of domains and serving as the basis for more advanced algorithms. Consequently, as the scale and complexity of modern applications continue to grow, the development of efficient and reliable QP algorithms is becoming increasingly vital. In this context, this paper introduces a novel deep learning-aided distributed optimization architecture designed for tackling large-scale QP problems. First, we combine the state-of-the-art Operator Splitting QP (OSQP) method with a consensus approach to derive DistributedQP, a new method tailored for network-structured problems, with convergence guarantees to optimality. Subsequently, we unfold this optimizer into a deep learning framework, leading to DeepDistributedQP, which leverages learned policies to accelerate reaching to desired accuracy within a restricted amount of iterations. Our approach is also theoretically grounded through Probably Approximately Correct (PAC)-Bayes theory, providing generalization bounds on the expected optimality gap for unseen problems. The proposed framework, as well as its centralized version DeepQP, significantly outperform their standard optimization counterparts on a variety of tasks such as randomly generated problems, optimal control, linear regression, transportation networks and others. Notably, DeepDistributedQP demonstrates strong generalization by training on small problems and scaling to solve much larger ones (up to 50K variables and 150K constraints) using the same policy. Moreover, it achieves orders-of-magnitude improvements in wall-clock time compared to OSQP. The certifiable performance guarantees of our approach are also demonstrated, ensuring higher-quality solutions over traditional optimizers.

Differentiable Robust Model Predictive Control

Deterministic model predictive control (MPC), while powerful, is often insufficient for effectively controlling autonomous systems in the real-world. Factors such as environmental noise and model error can cause deviations from the expected nominal performance. Robust MPC algorithms aim to bridge this gap between deterministic and uncertain control. However, these methods are often excessively difficult to tune for robustness due to the nonlinear and non-intuitive effects that controller parameters have on performance. To address this challenge, a unifying perspective on differentiable optimization for control is presented, which enables derivation of a general, differentiable tube-based MPC algorithm. The proposed approach facilitates the automatic and real-time tuning of robust controllers in the presence of large uncertainties and disturbances.

Parameterized Differential Dynamic Programming

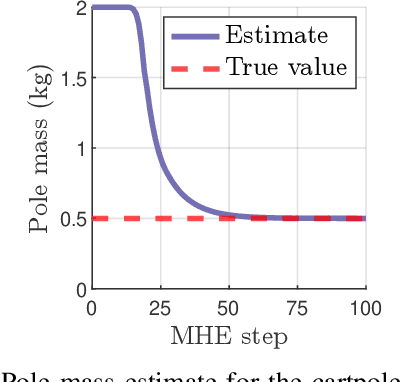
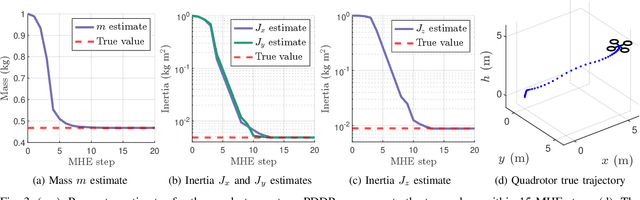
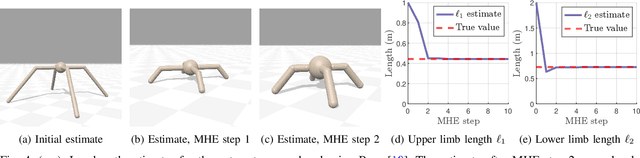
Differential Dynamic Programming (DDP) is an efficient trajectory optimization algorithm relying on second-order approximations of a system's dynamics and cost function, and has recently been applied to optimize systems with time-invariant parameters. Prior works include system parameter estimation and identifying the optimal switching time between modes of hybrid dynamical systems. This paper generalizes previous work by proposing a general parameterized optimal control objective and deriving a parametric version of DDP, titled Parameterized Differential Dynamic Programming (PDDP). A rigorous convergence analysis of the algorithm is provided, and PDDP is shown to converge to a minimum of the cost regardless of initialization. The effects of varying the optimization to more effectively escape local minima are analyzed. Experiments are presented applying PDDP on multiple robotics systems to solve model predictive control (MPC) and moving horizon estimation (MHE) tasks simultaneously. Finally, PDDP is used to determine the optimal transition point between flight regimes of a complex urban air mobility (UAM) class vehicle exhibiting multiple phases of flight.