Nearly Optimal Nonlinear Safe Control with BaS-SDRE

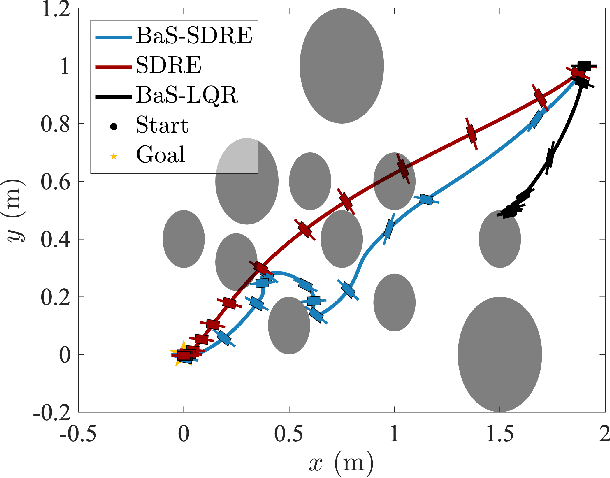
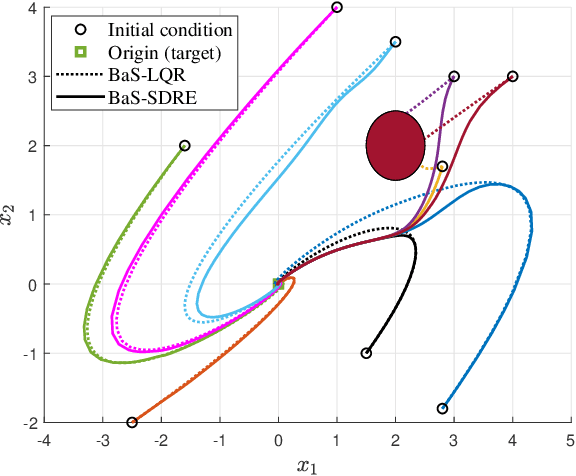
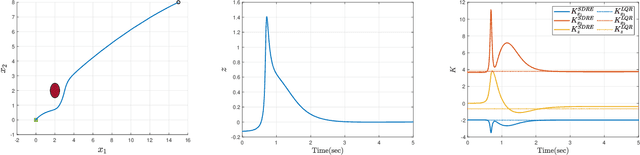
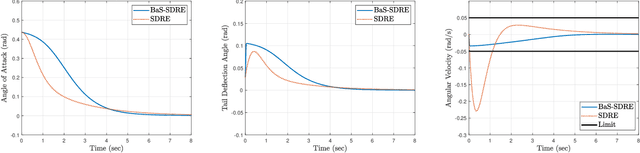
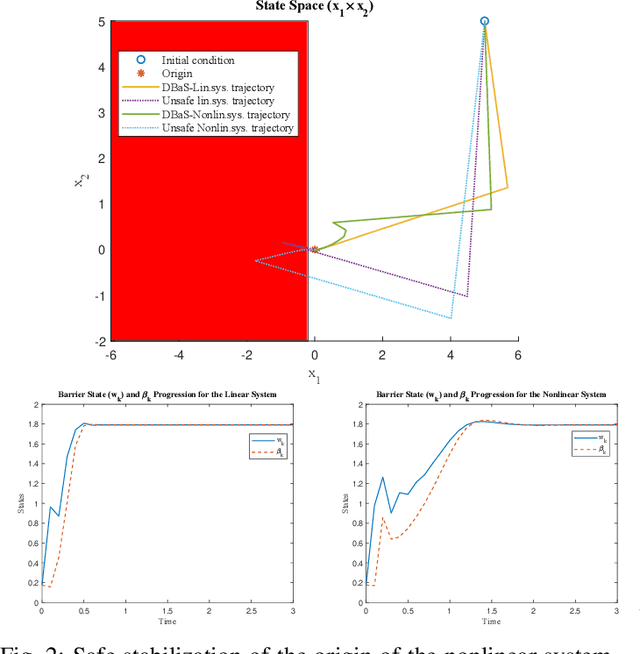
The State-Dependent Riccati Equation (SDRE) approach has emerged as a systematic and effective means of designing nearly optimal nonlinear controllers. The Barrier States (BaS) embedding methodology was developed recently for safe multi-objective controls in which the safety condition is manifested as a state to be controlled along with other states of the system. The overall system, termed the safety embedded system, is highly nonlinear even if the original system is linear. This paper develops a nonlinear nearly optimal safe feedback control technique by combining the two strategies effectively. First, the BaS is derived in an extended linearization formulation to be subsequently used to form an extended safety embedded system. A new optimal control problem is formed thereafter, which is used to construct a safety embedded State-Dependent Riccati Equation, termed BaS-SDRE, whose solution approximates the solution of the optimal control problem's associated Hamilton-Jacobi-Bellman (HJB) equation. The BaS-SDRE is then solved online to synthesize the nearly optimal safe control. The proposed technique's efficacy is demonstrated on an unstable, constrained linear system that shows how the synthesized control reacts to nonlinearities near the unsafe region, a nonlinear flight control system with limited path angular velocity that exists due to structural and dynamic concerns, and a planar quadrotor system that navigates safely in a crowded environment.

Gaussian Process Barrier States for Safe Trajectory Optimization and Control

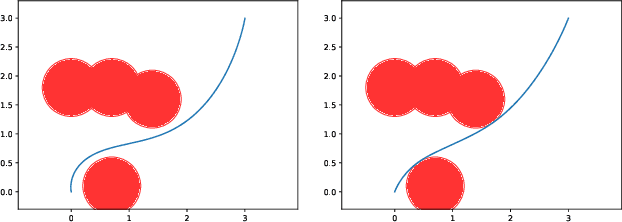
This paper proposes embedded Gaussian Process Barrier States (GP-BaS), a methodology to safely control unmodeled dynamics of nonlinear system using Bayesian learning. Gaussian Processes (GPs) are used to model the dynamics of the safety-critical system, which is subsequently used in the GP-BaS model. We derive the barrier state dynamics utilizing the GP posterior, which is used to construct a safety embedded Gaussian process dynamical model (GPDM). We show that the safety-critical system can be controlled to remain inside the safe region as long as we can design a controller that renders the BaS-GPDM's trajectories bounded (or asymptotically stable). The proposed approach overcomes various limitations in early attempts at combining GPs with barrier functions due to the abstention of restrictive assumptions such as linearity of the system with respect to control, relative degree of the constraints and number or nature of constraints. This work is implemented on various examples for trajectory optimization and control including optimal stabilization of unstable linear system and safe trajectory optimization of a Dubins vehicle navigating through an obstacle course and on a quadrotor in an obstacle avoidance task using GP differentiable dynamic programming (GP-DDP). The proposed framework is capable of maintaining safe optimization and control of unmodeled dynamics and is purely data driven.

Safety Embedded Differential Dynamic Programming using Discrete Barrier States

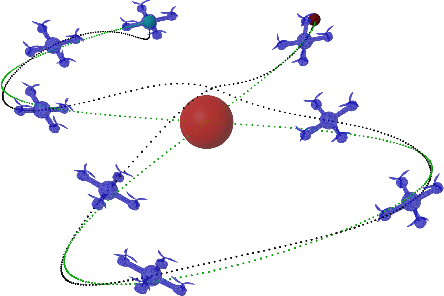
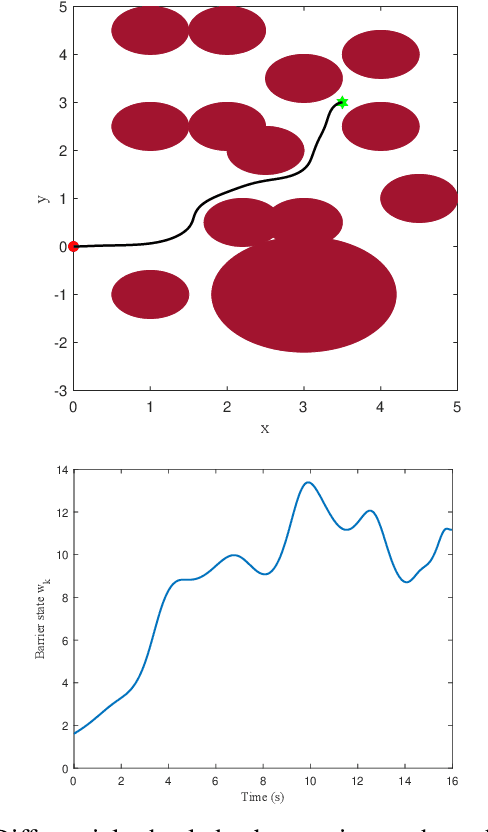
Certified safe control is a growing challenge in robotics, especially when performance and safety objectives are desired to be concurrently achieved. In this work, we extend the barrier state (BaS) concept, recently proposed for stabilization of continuous time systems, to enforce safety for discrete time systems by creating a discrete barrier state (DBaS). The constructed DBaS is embedded into the discrete model of the safety-critical system in order to integrate safety objectives into performance objectives. We subsequently use the proposed technique to implement a safety embedded stabilizing control for nonlinear discrete systems. Furthermore, we employ the DBaS method to develop a safety embedded differential dynamic programming (DDP) technique to plan and execute safe optimal trajectories. The proposed algorithm is leveraged on a differential wheeled robot and on a quadrotor to safely perform several tasks including reaching, tracking and safe multi-quadrotor movement. The DBaS-based DDP (DBaS-DDP) is compared to the penalty method used in constrained DDP problems where it is shown that the DBaS-DDP consistently outperforms the penalty method.