Admissibility Over Winning: A New Approach to Reactive Synthesis in Robotics

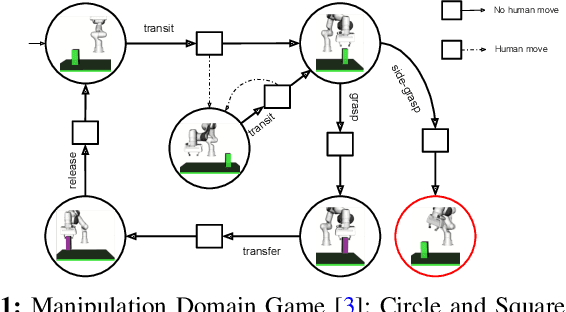
Reactive synthesis is a framework for modeling and automatically synthesizing strategies in robotics, typically through computing a \emph{winning} strategy in a 2-player game between the robot and the environment. Winning strategies, however, do not always exist, even in some simple cases. In such situations, it is still desirable for the robot to attempt its task rather than "giving up". In this work, we explore the notion of admissibility to define strategies beyond winning, tailored specifically for robotic systems. We introduce an ordering of admissible strategies and define \emph{admissibly rational strategies}, which aim to be winning and cooperative when possible, and non-violating and hopeful when necessary. We present an efficient synthesis algorithm and demonstrate that admissibly rational strategies produce desirable behaviors through case studies.

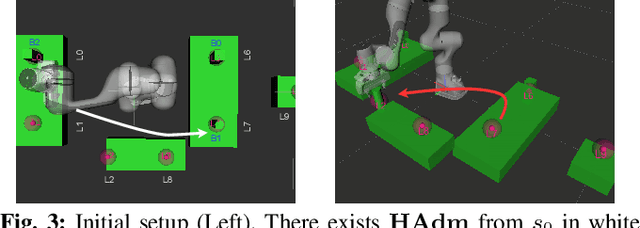
Beyond Winning Strategies: Admissible and Admissible Winning Strategies for Quantitative Reachability Games

Classical reactive synthesis approaches aim to synthesize a reactive system that always satisfies a given specifications. These approaches often reduce to playing a two-player zero-sum game where the goal is to synthesize a winning strategy. However, in many pragmatic domains, such as robotics, a winning strategy does not always exist, yet it is desirable for the system to make an effort to satisfy its requirements instead of "giving up". To this end, this paper investigates the notion of admissible strategies, which formalize "doing-your-best", in quantitative reachability games. We show that, unlike the qualitative case, quantitative admissible strategies are history-dependent even for finite payoff functions, making synthesis a challenging task. In addition, we prove that admissible strategies always exist but may produce undesirable optimistic behaviors. To mitigate this, we propose admissible winning strategies, which enforce the best possible outcome while being admissible. We show that both strategies always exist but are not memoryless. We provide necessary and sufficient conditions for the existence of both strategies and propose synthesis algorithms. Finally, we illustrate the strategies on gridworld and robot manipulator domains.

Stochastic Games for Interactive Manipulation Domains

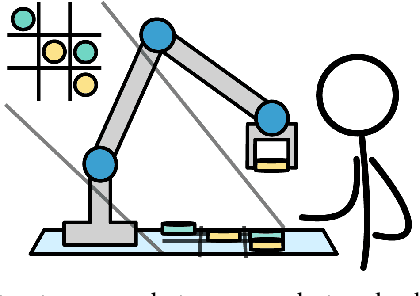
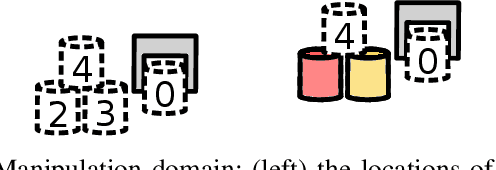
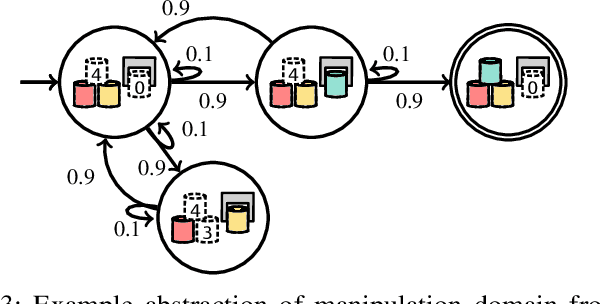
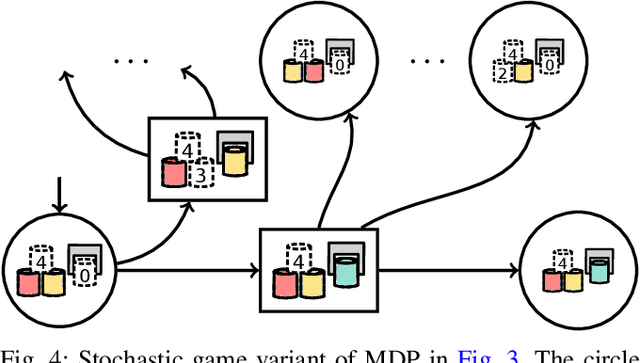
As robots become more prevalent, the complexity of robot-robot, robot-human, and robot-environment interactions increases. In these interactions, a robot needs to consider not only the effects of its own actions, but also the effects of other agents' actions and the possible interactions between agents. Previous works have considered reactive synthesis, where the human/environment is modeled as a deterministic, adversarial agent; as well as probabilistic synthesis, where the human/environment is modeled via a Markov chain. While they provide strong theoretical frameworks, there are still many aspects of human-robot interaction that cannot be fully expressed and many assumptions that must be made in each model. In this work, we propose stochastic games as a general model for human-robot interaction, which subsumes the expressivity of all previous representations. In addition, it allows us to make fewer modeling assumptions and leads to more natural and powerful models of interaction. We introduce the semantics of this abstraction and show how existing tools can be utilized to synthesize strategies to achieve complex tasks with guarantees. Further, we discuss the current computational limitations and improve the scalability by two orders of magnitude by a new way of constructing models for PRISM-games.

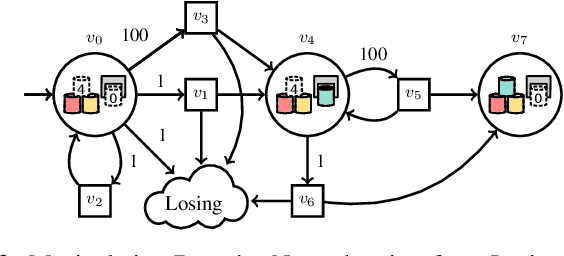
Efficient Symbolic Approaches for Quantitative Reactive Synthesis with Finite Tasks

This work introduces efficient symbolic algorithms for quantitative reactive synthesis. We consider resource-constrained robotic manipulators that need to interact with a human to achieve a complex task expressed in linear temporal logic. Our framework generates reactive strategies that not only guarantee task completion but also seek cooperation with the human when possible. We model the interaction as a two-player game and consider regret-minimizing strategies to encourage cooperation. We use symbolic representation of the game to enable scalability. For synthesis, we first introduce value iteration algorithms for such games with min-max objectives. Then, we extend our method to the regret-minimizing objectives. Our benchmarks reveal that our symbolic framework not only significantly improves computation time (up to an order of magnitude) but also can scale up to much larger instances of manipulation problems with up to 2x number of objects and locations than the state of the art.

Safety Guarantees for Neural Network Dynamic Systems via Stochastic Barrier Functions

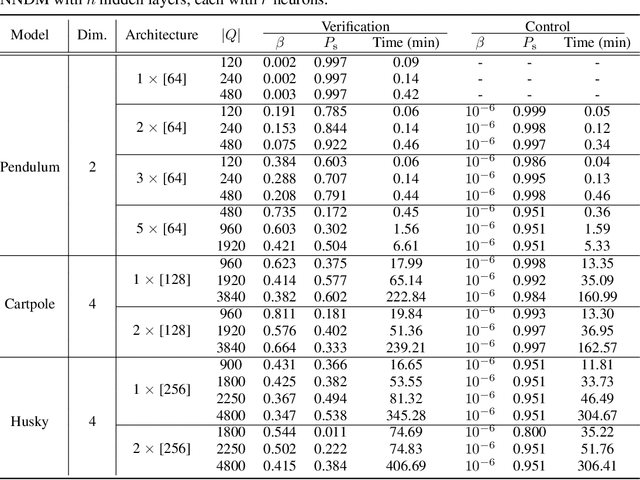
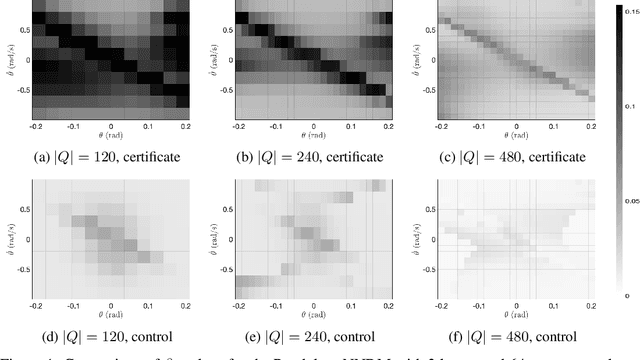
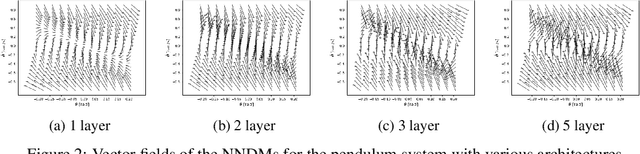
Neural Networks (NNs) have been successfully employed to represent the state evolution of complex dynamical systems. Such models, referred to as NN dynamic models (NNDMs), use iterative noisy predictions of NN to estimate a distribution of system trajectories over time. Despite their accuracy, safety analysis of NNDMs is known to be a challenging problem and remains largely unexplored. To address this issue, in this paper, we introduce a method of providing safety guarantees for NNDMs. Our approach is based on stochastic barrier functions, whose relation with safety are analogous to that of Lyapunov functions with stability. We first show a method of synthesizing stochastic barrier functions for NNDMs via a convex optimization problem, which in turn provides a lower bound on the system's safety probability. A key step in our method is the employment of the recent convex approximation results for NNs to find piece-wise linear bounds, which allow the formulation of the barrier function synthesis problem as a sum-of-squares optimization program. If the obtained safety probability is above the desired threshold, the system is certified. Otherwise, we introduce a method of generating controls for the system that robustly maximizes the safety probability in a minimally-invasive manner. We exploit the convexity property of the barrier function to formulate the optimal control synthesis problem as a linear program. Experimental results illustrate the efficacy of the method. Namely, they show that the method can scale to multi-dimensional NNDMs with multiple layers and hundreds of neurons per layer, and that the controller can significantly improve the safety probability.

Let's Collaborate: Regret-based Reactive Synthesis for Robotic Manipulation

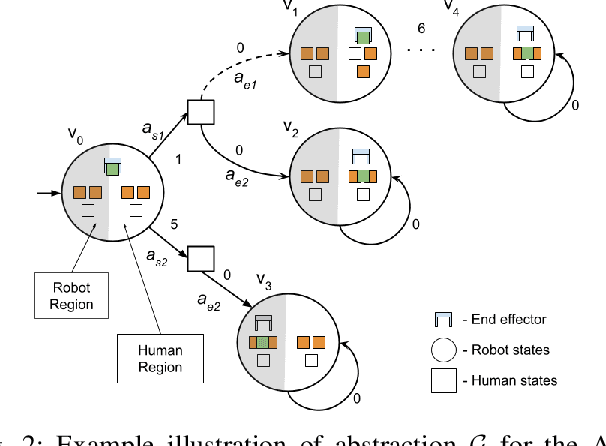
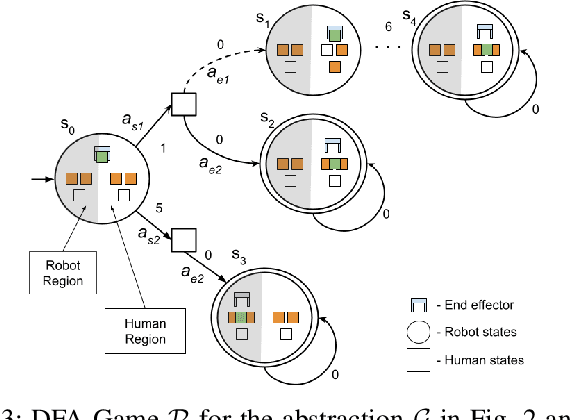
As robots gain capabilities to enter our human-centric world, they require formalism and algorithms that enable smart and efficient interactions. This is challenging, especially for robotic manipulators with complex tasks that may require collaboration with humans. Prior works approach this problem through reactive synthesis and generate strategies for the robot that guarantee task completion by assuming an adversarial human. While this assumption gives a sound solution, it leads to an "unfriendly" robot that is agnostic to the human intentions. We relax this assumption by formulating the problem using the notion of regret. We identify an appropriate definition for regret and develop regret-minimizing synthesis framework that enables the robot to seek cooperation when possible while preserving task completion guarantees. We illustrate the efficacy of our framework via various case studies.