Data-Driven Permissible Safe Control with Barrier Certificates

This paper introduces a method of identifying a maximal set of safe strategies from data for stochastic systems with unknown dynamics using barrier certificates. The first step is learning the dynamics of the system via Gaussian process (GP) regression and obtaining probabilistic errors for this estimate. Then, we develop an algorithm for constructing piecewise stochastic barrier functions to find a maximal permissible strategy set using the learned GP model, which is based on sequentially pruning the worst controls until a maximal set is identified. The permissible strategies are guaranteed to maintain probabilistic safety for the true system. This is especially important for learning-enabled systems, because a rich strategy space enables additional data collection and complex behaviors while remaining safe. Case studies on linear and nonlinear systems demonstrate that increasing the size of the dataset for learning the system grows the permissible strategy set.

Piecewise Stochastic Barrier Functions

This paper presents a novel stochastic barrier function (SBF) framework for safety analysis of stochastic systems based on piecewise (PW) functions. We first outline a general formulation of PW-SBFs. Then, we focus on PW-Constant (PWC) SBFs and show how their simplicity yields computational advantages for general stochastic systems. Specifically, we prove that synthesis of PWC-SBFs reduces to a minimax optimization problem. Then, we introduce three efficient algorithms to solve this problem, each offering distinct advantages and disadvantages. The first algorithm is based on dual linear programming (LP), which provides an exact solution to the minimax optimization problem. The second is a more scalable algorithm based on iterative counter-example guided synthesis, which involves solving two smaller LPs. The third algorithm solves the minimax problem using gradient descent, which admits even better scalability. We provide an extensive evaluation of these methods on various case studies, including neural network dynamic models, nonlinear switched systems, and high-dimensional linear systems. Our benchmarks demonstrate that PWC-SBFs outperform state-of-the-art methods, namely sum-of-squares and neural barrier functions, and can scale to eight dimensional systems.

Safety Guarantees for Neural Network Dynamic Systems via Stochastic Barrier Functions

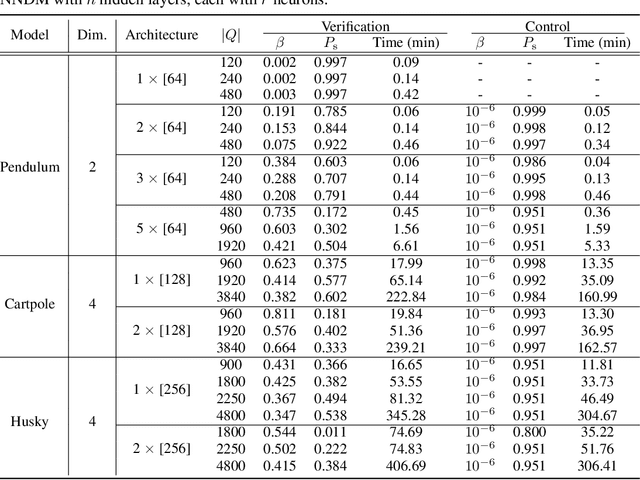
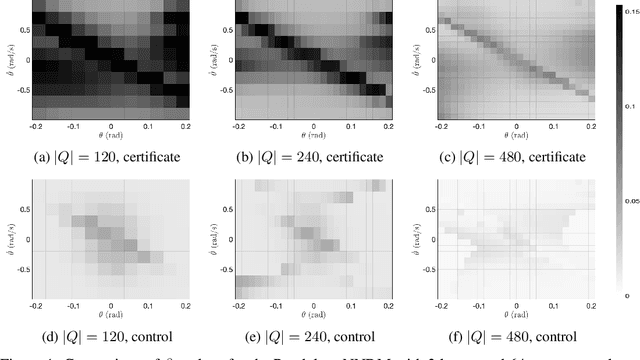
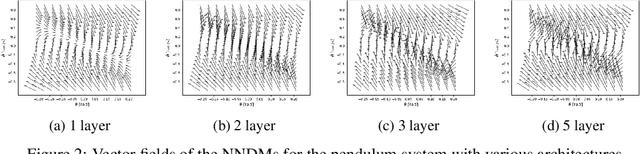
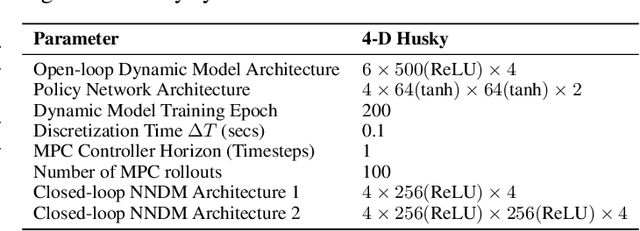
Neural Networks (NNs) have been successfully employed to represent the state evolution of complex dynamical systems. Such models, referred to as NN dynamic models (NNDMs), use iterative noisy predictions of NN to estimate a distribution of system trajectories over time. Despite their accuracy, safety analysis of NNDMs is known to be a challenging problem and remains largely unexplored. To address this issue, in this paper, we introduce a method of providing safety guarantees for NNDMs. Our approach is based on stochastic barrier functions, whose relation with safety are analogous to that of Lyapunov functions with stability. We first show a method of synthesizing stochastic barrier functions for NNDMs via a convex optimization problem, which in turn provides a lower bound on the system's safety probability. A key step in our method is the employment of the recent convex approximation results for NNs to find piece-wise linear bounds, which allow the formulation of the barrier function synthesis problem as a sum-of-squares optimization program. If the obtained safety probability is above the desired threshold, the system is certified. Otherwise, we introduce a method of generating controls for the system that robustly maximizes the safety probability in a minimally-invasive manner. We exploit the convexity property of the barrier function to formulate the optimal control synthesis problem as a linear program. Experimental results illustrate the efficacy of the method. Namely, they show that the method can scale to multi-dimensional NNDMs with multiple layers and hundreds of neurons per layer, and that the controller can significantly improve the safety probability.