Piecewise Stochastic Barrier Functions
Paper and Code
Apr 29, 2024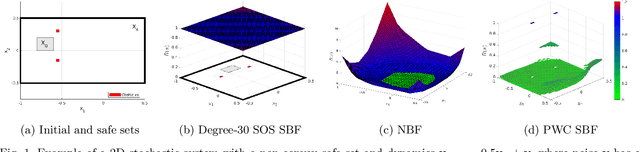
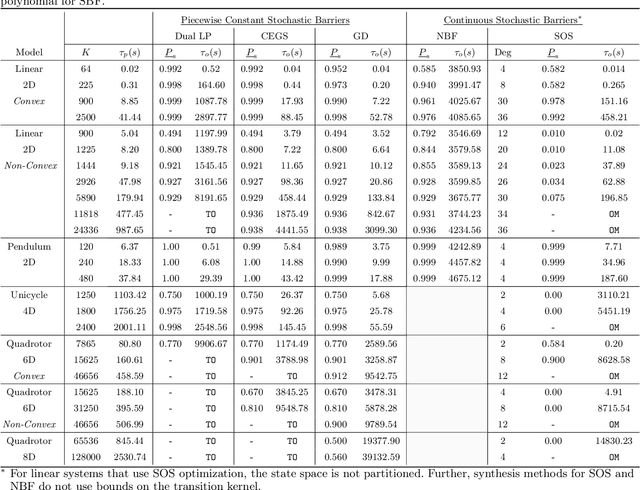
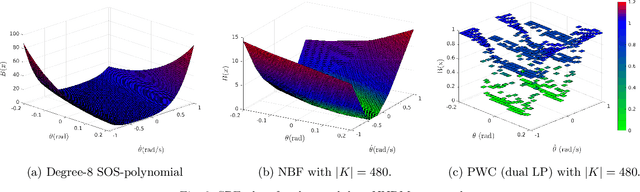
This paper presents a novel stochastic barrier function (SBF) framework for safety analysis of stochastic systems based on piecewise (PW) functions. We first outline a general formulation of PW-SBFs. Then, we focus on PW-Constant (PWC) SBFs and show how their simplicity yields computational advantages for general stochastic systems. Specifically, we prove that synthesis of PWC-SBFs reduces to a minimax optimization problem. Then, we introduce three efficient algorithms to solve this problem, each offering distinct advantages and disadvantages. The first algorithm is based on dual linear programming (LP), which provides an exact solution to the minimax optimization problem. The second is a more scalable algorithm based on iterative counter-example guided synthesis, which involves solving two smaller LPs. The third algorithm solves the minimax problem using gradient descent, which admits even better scalability. We provide an extensive evaluation of these methods on various case studies, including neural network dynamic models, nonlinear switched systems, and high-dimensional linear systems. Our benchmarks demonstrate that PWC-SBFs outperform state-of-the-art methods, namely sum-of-squares and neural barrier functions, and can scale to eight dimensional systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge