Data-Driven Permissible Safe Control with Barrier Certificates

This paper introduces a method of identifying a maximal set of safe strategies from data for stochastic systems with unknown dynamics using barrier certificates. The first step is learning the dynamics of the system via Gaussian process (GP) regression and obtaining probabilistic errors for this estimate. Then, we develop an algorithm for constructing piecewise stochastic barrier functions to find a maximal permissible strategy set using the learned GP model, which is based on sequentially pruning the worst controls until a maximal set is identified. The permissible strategies are guaranteed to maintain probabilistic safety for the true system. This is especially important for learning-enabled systems, because a rich strategy space enables additional data collection and complex behaviors while remaining safe. Case studies on linear and nonlinear systems demonstrate that increasing the size of the dataset for learning the system grows the permissible strategy set.

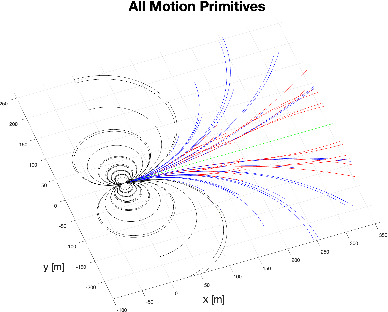
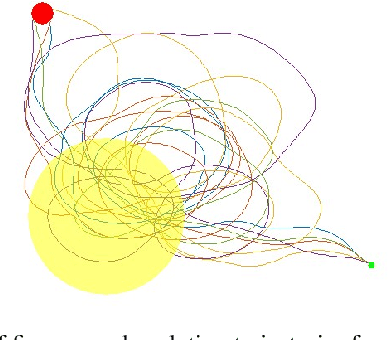
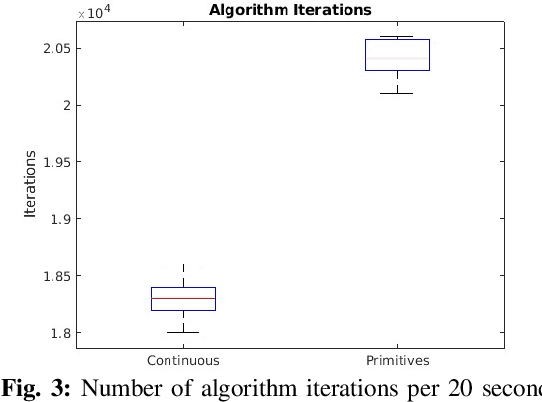
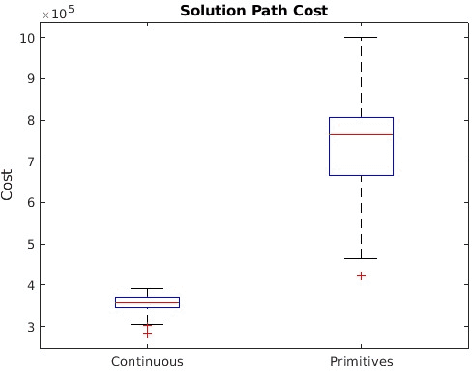
Path Planning in 3D with Motion Primitives for Wind Energy-Harvesting Fixed-Wing Aircraft

In this work, a set of motion primitives is defined for use in an energy-aware motion planning problem. The motion primitives are defined as sequences of control inputs to a simplified four-DOF dynamics model and are used to replace the traditional continuous control space used in many sampling-based motion planners. The primitives are implemented in a Stable Sparse Rapidly Exploring Random Tree (SST) motion planner and compared to an identical planner using a continuous control space. The planner using primitives was found to run 11.0\% faster but yielded solution paths that were on average worse with higher variance. Also, the solution path travel time is improved by about 50\%. Using motion primitives for sampling spaces in SST can effectively reduce the run time of the algorithm, although at the cost of solution quality.

Formal Verification of Unknown Dynamical Systems via Gaussian Process Regression

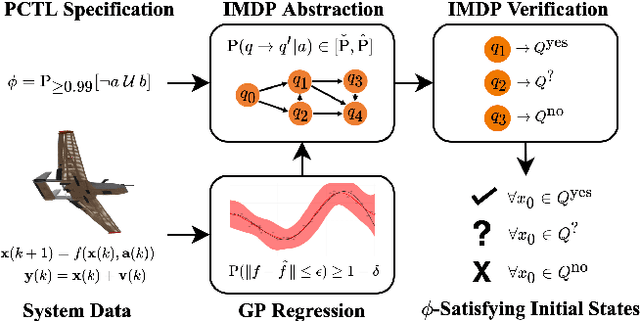
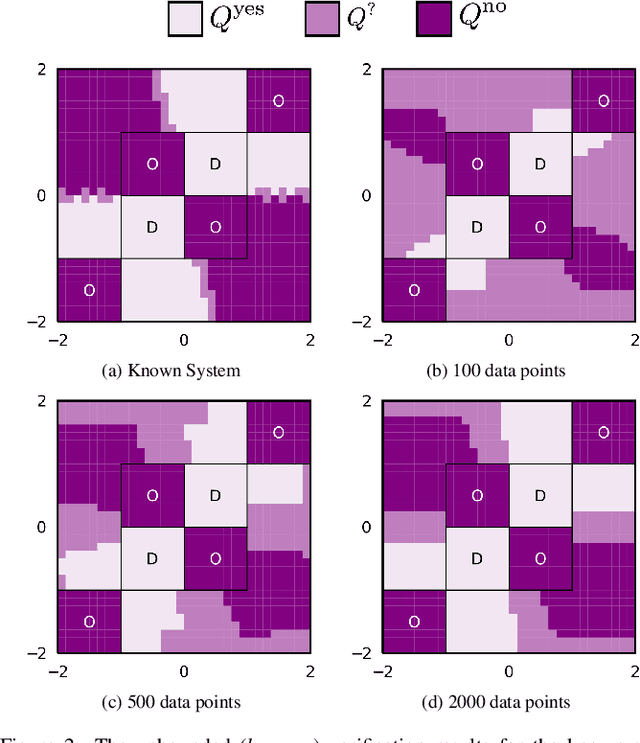
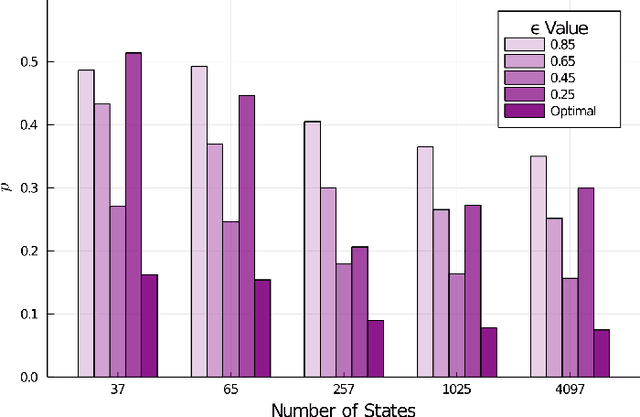
Leveraging autonomous systems in safety-critical scenarios requires verifying their behaviors in the presence of uncertainties and black-box components that influence the system dynamics. In this article, we develop a framework for verifying partially-observable, discrete-time dynamical systems with unmodelled dynamics against temporal logic specifications from a given input-output dataset. The verification framework employs Gaussian process (GP) regression to learn the unknown dynamics from the dataset and abstract the continuous-space system as a finite-state, uncertain Markov decision process (MDP). This abstraction relies on space discretization and transition probability intervals that capture the uncertainty due to the error in GP regression by using reproducible kernel Hilbert space analysis as well as the uncertainty induced by discretization. The framework utilizes existing model checking tools for verification of the uncertain MDP abstraction against a given temporal logic specification. We establish the correctness of extending the verification results on the abstraction to the underlying partially-observable system. We show that the computational complexity of the framework is polynomial in the size of the dataset and discrete abstraction. The complexity analysis illustrates a trade-off between the quality of the verification results and the computational burden to handle larger datasets and finer abstractions. Finally, we demonstrate the efficacy of our learning and verification framework on several case studies with linear, nonlinear, and switched dynamical systems.

Factorized Machine Self-Confidence for Decision-Making Agents

Algorithmic assurances from advanced autonomous systems assist human users in understanding, trusting, and using such systems appropriately. Designing these systems with the capacity of assessing their own capabilities is one approach to creating an algorithmic assurance. The idea of `machine self-confidence' is introduced for autonomous systems. Using a factorization based framework for self-confidence assessment, one component of self-confidence, called `solver-quality', is discussed in the context of Markov decision processes for autonomous systems. Markov decision processes underlie much of the theory of reinforcement learning, and are commonly used for planning and decision making under uncertainty in robotics and autonomous systems. A `solver quality' metric is formally defined in the context of decision making algorithms based on Markov decision processes. A method for assessing solver quality is then derived, drawing inspiration from empirical hardness models. Finally, numerical experiments for an unmanned autonomous vehicle navigation problem under different solver, parameter, and environment conditions indicate that the self-confidence metric exhibits the desired properties. Discussion of results, and avenues for future investigation are included.