Error Bounds for Deep Learning-based Uncertainty Propagation in SDEs

Stochastic differential equations are commonly used to describe the evolution of stochastic processes. The uncertainty of such processes is best represented by the probability density function (PDF), whose evolution is governed by the Fokker-Planck partial differential equation (FP-PDE). However, it is generally infeasible to solve the FP-PDE in closed form. In this work, we show that physics-informed neural networks (PINNs) can be trained to approximate the solution PDF using existing methods. The main contribution is the analysis of the approximation error: we develop a theory to construct an arbitrary tight error bound with PINNs. In addition, we derive a practical error bound that can be efficiently constructed with existing training methods. Finally, we explain that this error-bound theory generalizes to approximate solutions of other linear PDEs. Several numerical experiments are conducted to demonstrate and validate the proposed methods.

Using Surprise Index for Competency Assessment in Autonomous Decision-Making

This paper considers the problem of evaluating an autonomous system's competency in performing a task, particularly when working in dynamic and uncertain environments. The inherent opacity of machine learning models, from the perspective of the user, often described as a `black box', poses a challenge. To overcome this, we propose using a measure called the Surprise index, which leverages available measurement data to quantify whether the dynamic system performs as expected. We show that the surprise index can be computed in closed form for dynamic systems when observed evidence in a probabilistic model if the joint distribution for that evidence follows a multivariate Gaussian marginal distribution. We then apply it to a nonlinear spacecraft maneuver problem, where actions are chosen by a reinforcement learning agent and show it can indicate how well the trajectory follows the required orbit.

Gravity Estimation at Small Bodies via Optical Tracking of Hopping Artificial Probes

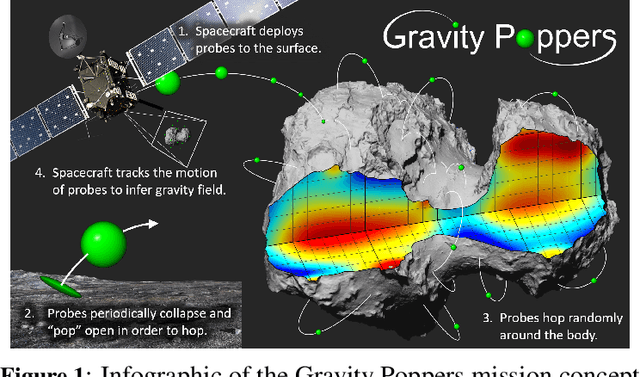
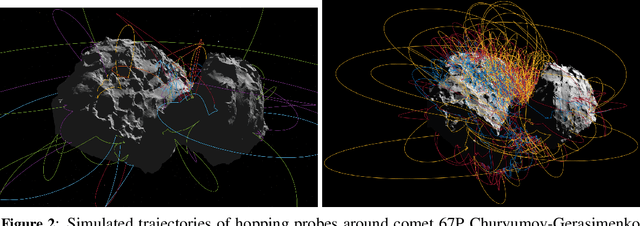
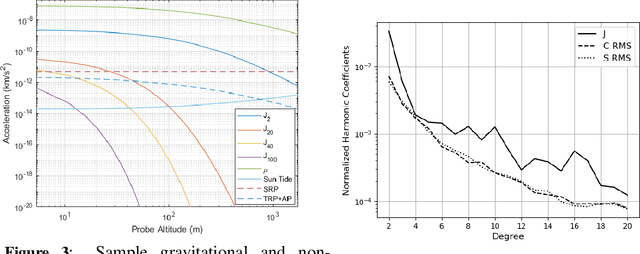
Despite numerous successful missions to small celestial bodies, the gravity field of such targets has been poorly characterized so far. Gravity estimates can be used to infer the internal structure and composition of small bodies and, as such, have strong implications in the fields of planetary science, planetary defense, and in-situ resource utilization. Current gravimetry techniques at small bodies mostly rely on tracking the spacecraft orbital motion, where the gravity observability is low. To date, only lower-degree and order spherical harmonics of small-body gravity fields could be resolved. In this paper, we evaluate gravimetry performance for a novel mission architecture where artificial probes repeatedly hop across the surface of the small body and perform low-altitude, suborbital arcs. Such probes are tracked using optical measurements from the mothership's onboard camera and orbit determination is performed to estimate the probe trajectories, the small body's rotational kinematics, and the gravity field. The suborbital motion of the probes provides dense observations at low altitude, where the gravity signal is stronger. We assess the impact of observation parameters and mission duration on gravity observability. Results suggest that the gravitational spherical harmonics of a small body with the same mass as the asteroid Bennu, can be observed at least up to degree 40 within months of observations. Measurement precision and frequency are key to achieve high-performance gravimetry.