Exact and Approximate Heterogeneous Bayesian Decentralized Data Fusion
Paper and Code
Jan 26, 2021

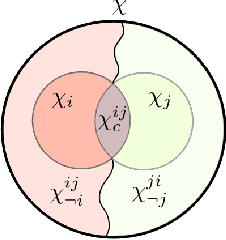
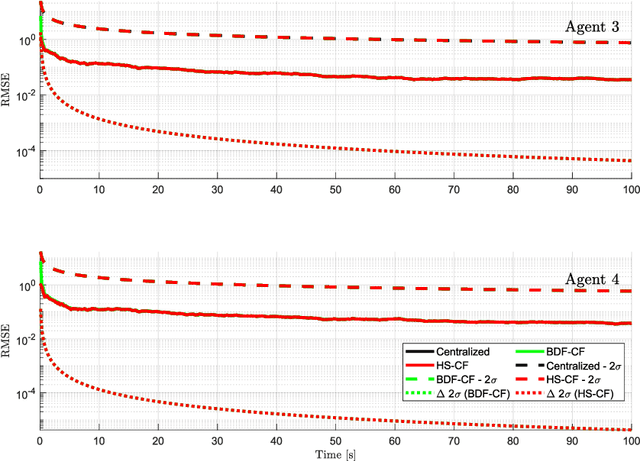
In Bayesian peer-to-peer decentralized data fusion for static and dynamic systems, the underlying estimated or communicated distributions are frequently assumed to be homogeneous between agents. This requires each agent to process and communicate the full global joint distribution, and thus leads to high computation and communication costs irrespective of relevancy to specific local objectives. This work considers a family of heterogeneous decentralized fusion problems, where we consider the set of problems in which either the communicated or the estimated distributions describe different, but overlapping, states of interest that are subsets of a larger full global joint state. We exploit the conditional independence structure of such problems and provide a rigorous derivation for a family of exact and approximate heterogeneous conditionally factorized channel filter methods. We further extend existing methods for approximate conservative filtering and decentralized fusion in heterogeneous dynamic problems. Numerical examples show more than 99.5% potential communication reduction for heterogeneous channel filter fusion, and a multi-target tracking simulation shows that these methods provide consistent estimates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge