Generalized Optimality Guarantees for Solving Continuous Observation POMDPs through Particle Belief MDP Approximation

Partially observable Markov decision processes (POMDPs) provide a flexible representation for real-world decision and control problems. However, POMDPs are notoriously difficult to solve, especially when the state and observation spaces are continuous or hybrid, which is often the case for physical systems. While recent online sampling-based POMDP algorithms that plan with observation likelihood weighting have shown practical effectiveness, a general theory bounding the approximation error of the particle filtering techniques that these algorithms use has not previously been proposed. Our main contribution is to formally justify that optimality guarantees in a finite sample particle belief MDP (PB-MDP) approximation of a POMDP/belief MDP yields optimality guarantees in the original POMDP as well. This fundamental bridge between PB-MDPs and POMDPs allows us to adapt any sampling-based MDP algorithm of choice to a POMDP by solving the corresponding particle belief MDP approximation and preserve the convergence guarantees in the POMDP. Practically, this means additionally assuming access to the observation density model, and simply swapping out the state transition generative model with a particle filtering-based model, which only increases the computational complexity by a factor of $\mathcal{O}(C)$, with $C$ the number of particles in a particle belief state. In addition to our theoretical contribution, we perform five numerical experiments on benchmark POMDPs to demonstrate that a simple MDP algorithm adapted using PB-MDP approximation, Sparse-PFT, achieves performance competitive with other leading continuous observation POMDP solvers.

Visual Learning-based Planning for Continuous High-Dimensional POMDPs

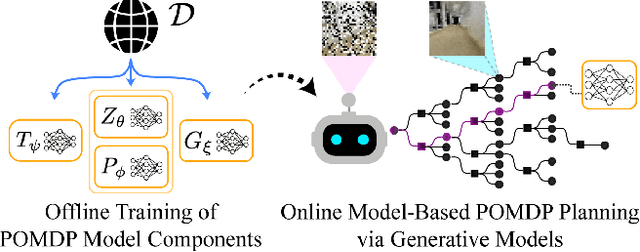
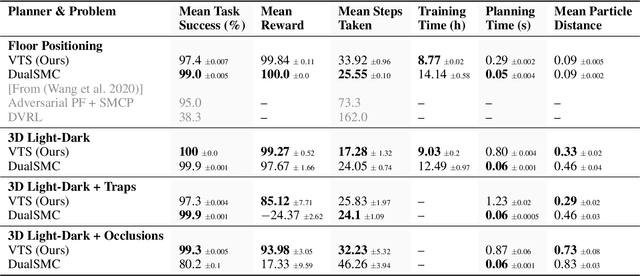
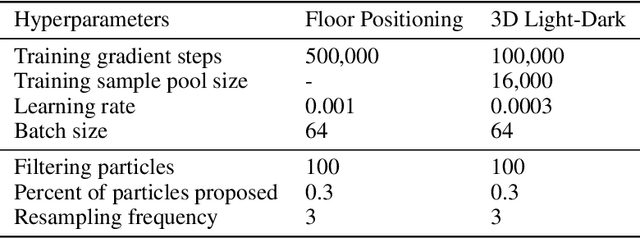
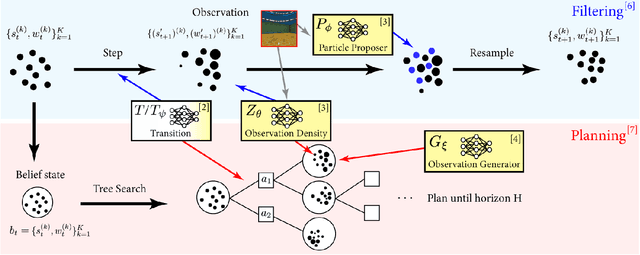
The Partially Observable Markov Decision Process (POMDP) is a powerful framework for capturing decision-making problems that involve state and transition uncertainty. However, most current POMDP planners cannot effectively handle very high-dimensional observations they often encounter in the real world (e.g. image observations in robotic domains). In this work, we propose Visual Tree Search (VTS), a learning and planning procedure that combines generative models learned offline with online model-based POMDP planning. VTS bridges offline model training and online planning by utilizing a set of deep generative observation models to predict and evaluate the likelihood of image observations in a Monte Carlo tree search planner. We show that VTS is robust to different observation noises and, since it utilizes online, model-based planning, can adapt to different reward structures without the need to re-train. This new approach outperforms a baseline state-of-the-art on-policy planning algorithm while using significantly less offline training time.

Multi-Task Learning with Sequence-Conditioned Transporter Networks

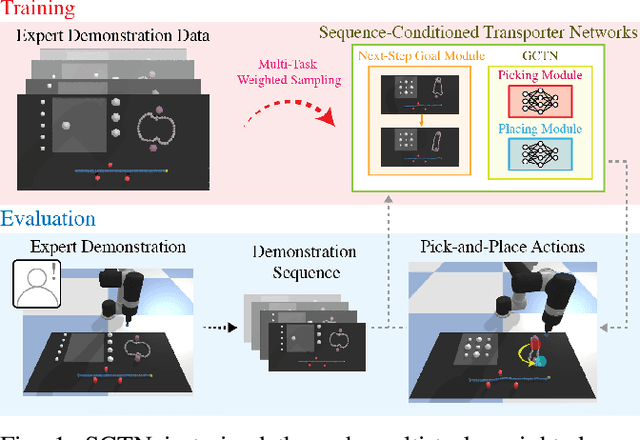
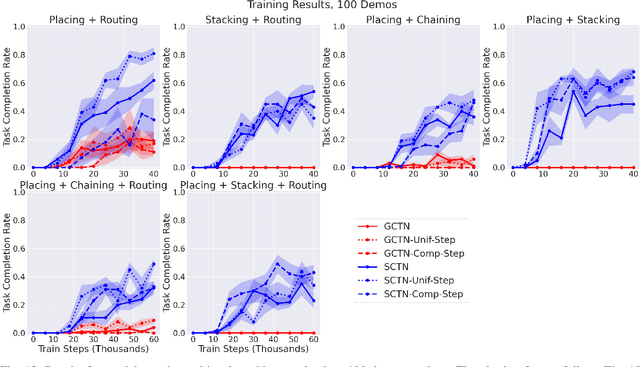
Enabling robots to solve multiple manipulation tasks has a wide range of industrial applications. While learning-based approaches enjoy flexibility and generalizability, scaling these approaches to solve such compositional tasks remains a challenge. In this work, we aim to solve multi-task learning through the lens of sequence-conditioning and weighted sampling. First, we propose a new suite of benchmark specifically aimed at compositional tasks, MultiRavens, which allows defining custom task combinations through task modules that are inspired by industrial tasks and exemplify the difficulties in vision-based learning and planning methods. Second, we propose a vision-based end-to-end system architecture, Sequence-Conditioned Transporter Networks, which augments Goal-Conditioned Transporter Networks with sequence-conditioning and weighted sampling and can efficiently learn to solve multi-task long horizon problems. Our analysis suggests that not only the new framework significantly improves pick-and-place performance on novel 10 multi-task benchmark problems, but also the multi-task learning with weighted sampling can vastly improve learning and agent performances on individual tasks.

Voronoi Progressive Widening: Efficient Online Solvers for Continuous Space MDPs and POMDPs with Provably Optimal Components

Markov decision processes (MDPs) and partially observable MDPs (POMDPs) can effectively represent complex real-world decision and control problems. However, continuous space MDPs and POMDPs, i.e. those having continuous state, action and observation spaces, are extremely difficult to solve, and there are few online algorithms with convergence guarantees. This paper introduces Voronoi Progressive Widening (VPW), a general technique to modify tree search algorithms to effectively handle continuous or hybrid action spaces, and proposes and evaluates three continuous space solvers: VOSS, VOWSS, and VOMCPOW. VOSS and VOWSS are theoretical tools based on sparse sampling and Voronoi optimistic optimization designed to justify VPW-based online solvers. While previous algorithms have enjoyed convergence guarantees for problems with continuous state and observation spaces, VOWSS is the first with global convergence guarantees for problems that additionally have continuous action spaces. VOMCPOW is a versatile and efficient VPW-based algorithm that consistently outperforms POMCPOW and BOMCP in several simulation experiments.

Sparse tree search optimality guarantees in POMDPs with continuous observation spaces

Partially observable Markov decision processes (POMDPs) with continuous state and observation spaces have powerful flexibility for representing real-world decision and control problems, but are notoriously difficult to solve. Recent online sampling-based algorithms that use observation likelihood weighting have shown unprecedented effectiveness in domains with continuous observation spaces. However there has been no formal theoretical justification for this technique. This work offers such a justification, proving that a simplified algorithm, partially observable weighted sparse sampling (POWSS), will estimate Q-values accurately with high probability and can be made to perform arbitrarily near the optimal solution by increasing computational power.