Gaussian Belief Trees for Chance Constrained Asymptotically Optimal Motion Planning
Paper and Code
Feb 24, 2022
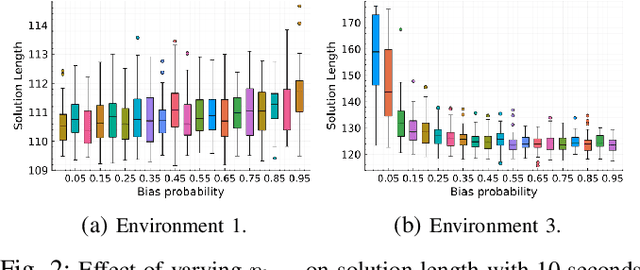
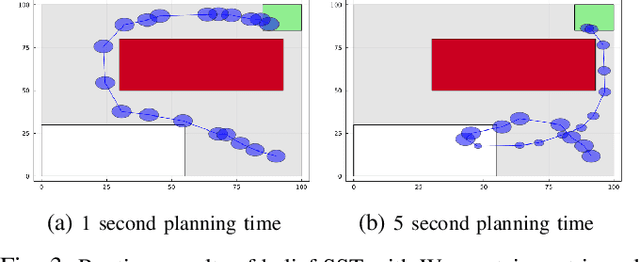
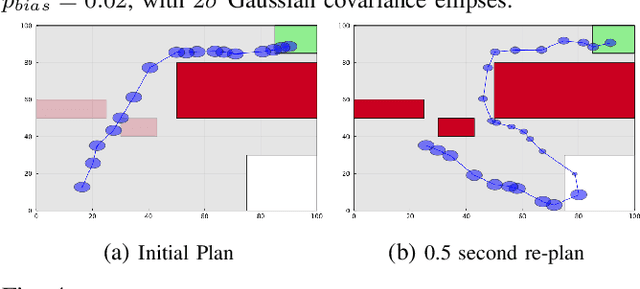
In this paper, we address the problem of sampling-based motion planning under motion and measurement uncertainty with probabilistic guarantees. We generalize traditional sampling-based tree-based motion planning algorithms for deterministic systems and propose belief-$\mathcal{A}$, a framework that extends any kinodynamical tree-based planner to the belief space for linear (or linearizable) systems. We introduce appropriate sampling techniques and distance metrics for the belief space that preserve the probabilistic completeness and asymptotic optimality properties of the underlying planner. We demonstrate the efficacy of our approach for finding safe low-cost paths efficiently and asymptotically optimally in simulation, for both holonomic and non-holonomic systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge