Previous Knowledge Utilization In Online Anytime Belief Space Planning

Online planning under uncertainty remains a critical challenge in robotics and autonomous systems. While tree search techniques are commonly employed to construct partial future trajectories within computational constraints, most existing methods discard information from previous planning sessions considering continuous spaces. This study presents a novel, computationally efficient approach that leverages historical planning data in current decision-making processes. We provide theoretical foundations for our information reuse strategy and introduce an algorithm based on Monte Carlo Tree Search (MCTS) that implements this approach. Experimental results demonstrate that our method significantly reduces computation time while maintaining high performance levels. Our findings suggest that integrating historical planning information can substantially improve the efficiency of online decision-making in uncertain environments, paving the way for more responsive and adaptive autonomous systems.

Anytime Probabilistically Constrained Provably Convergent Online Belief Space Planning

Taking into account future risk is essential for an autonomously operating robot to find online not only the best but also a safe action to execute. In this paper, we build upon the recently introduced formulation of probabilistic belief-dependent constraints. We present an anytime approach employing the Monte Carlo Tree Search (MCTS) method in continuous domains. Unlike previous approaches, our method assures safety anytime with respect to the currently expanded search tree without relying on the convergence of the search. We prove convergence in probability with an exponential rate of a version of our algorithms and study proposed techniques via extensive simulations. Even with a tiny number of tree queries, the best action found by our approach is much safer than the baseline. Moreover, our approach constantly finds better than the baseline action in terms of objective. This is because we revise the values and statistics maintained in the search tree and remove from them the contribution of the pruned actions.

Simplified POMDP Planning with an Alternative Observation Space and Formal Performance Guarantees

Online planning under uncertainty in partially observable domains is an essential capability in robotics and AI. The partially observable Markov decision process (POMDP) is a mathematically principled framework for addressing decision-making problems in this challenging setting. However, finding an optimal solution for POMDPs is computationally expensive and is feasible only for small problems. In this work, we contribute a novel method to simplify POMDPs by switching to an alternative, more compact, observation space and simplified model to speedup planning with formal performance guarantees. We introduce the notion of belief tree topology, which encodes the levels and branches in the tree that use the original and alternative observation space and models. Each belief tree topology comes with its own policy space and planning performance. Our key contribution is to derive bounds between the optimal Q-function of the original POMDP and the simplified tree defined by a given topology with a corresponding simplified policy space. These bounds are then used as an adaptation mechanism between different tree topologies until the optimal action of the original POMDP can be determined. Further, we consider a specific instantiation of our framework, where the alternative observation space and model correspond to a setting where the state is fully observable. We evaluate our approach in simulation, considering exact and approximate POMDP solvers and demonstrating a significant speedup while preserving solution quality. We believe this work opens new exciting avenues for online POMDP planning with formal performance guarantees.

Simplification of Risk Averse POMDPs with Performance Guarantees

Risk averse decision making under uncertainty in partially observable domains is a fundamental problem in AI and essential for reliable autonomous agents. In our case, the problem is modeled using partially observable Markov decision processes (POMDPs), when the value function is the conditional value at risk (CVaR) of the return. Calculating an optimal solution for POMDPs is computationally intractable in general. In this work we develop a simplification framework to speedup the evaluation of the value function, while providing performance guarantees. We consider as simplification a computationally cheaper belief-MDP transition model, that can correspond, e.g., to cheaper observation or transition models. Our contributions include general bounds for CVaR that allow bounding the CVaR of a random variable X, using a random variable Y, by assuming bounds between their cumulative distributions. We then derive bounds for the CVaR value function in a POMDP setting, and show how to bound the value function using the computationally cheaper belief-MDP transition model and without accessing the computationally expensive model in real-time. Then, we provide theoretical performance guarantees for the estimated bounds. Our results apply for a general simplification of a belief-MDP transition model and support simplification of both the observation and state transition models simultaneously.

A Slices Perspective for Incremental Nonparametric Inference in High Dimensional State Spaces

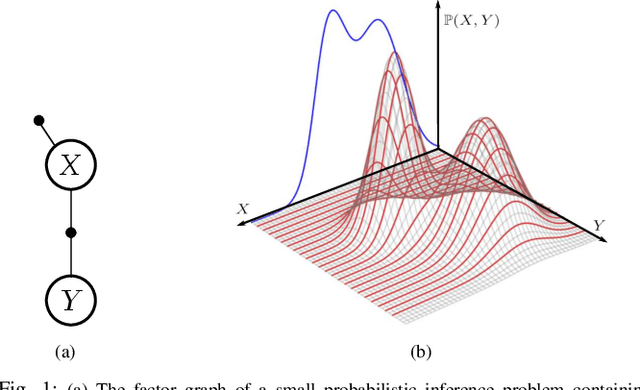
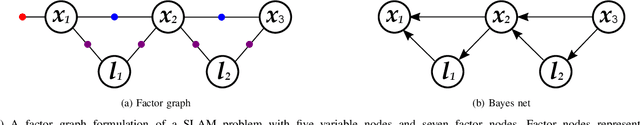
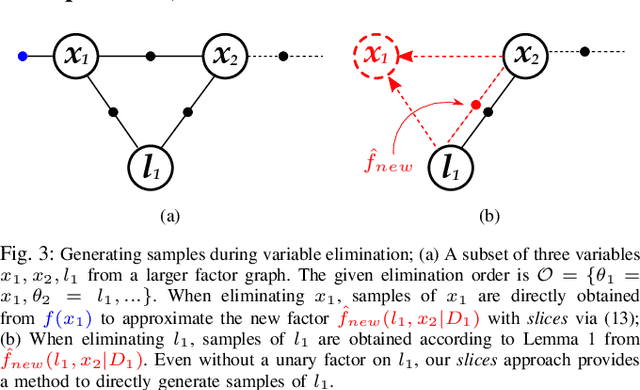
We introduce an innovative method for incremental nonparametric probabilistic inference in high-dimensional state spaces. Our approach leverages \slices from high-dimensional surfaces to efficiently approximate posterior distributions of any shape. Unlike many existing graph-based methods, our \slices perspective eliminates the need for additional intermediate reconstructions, maintaining a more accurate representation of posterior distributions. Additionally, we propose a novel heuristic to balance between accuracy and efficiency, enabling real-time operation in nonparametric scenarios. In empirical evaluations on synthetic and real-world datasets, our \slices approach consistently outperforms other state-of-the-art methods. It demonstrates superior accuracy and achieves a significant reduction in computational complexity, often by an order of magnitude.

Multi-Robot Communication-Aware Cooperative Belief Space Planning with Inconsistent Beliefs: An Action-Consistent Approach

Multi-robot belief space planning (MR-BSP) is essential for reliable and safe autonomy. While planning, each robot maintains a belief over the state of the environment and reasons how the belief would evolve in the future for different candidate actions. Yet, existing MR-BSP works have a common assumption that the beliefs of different robots are consistent at planning time. Such an assumption is often highly unrealistic, as it requires prohibitively extensive and frequent communication capabilities. In practice, each robot may have a different belief about the state of the environment. Crucially, when the beliefs of different robots are inconsistent, state-of-the-art MR-BSP approaches could result in a lack of coordination between the robots, and in general, could yield dangerous, unsafe and sub-optimal decisions. In this paper, we tackle this crucial gap. We develop a novel decentralized algorithm that is guaranteed to find a consistent joint action. For a given robot, our algorithm reasons for action preferences about 1) its local information, 2) what it perceives about the reasoning of the other robot, and 3) what it perceives about the reasoning of itself perceived by the other robot. This algorithm finds a consistent joint action whenever these steps yield the same best joint action obtained by reasoning about action preferences; otherwise, it self-triggers communication between the robots. Experimental results show efficacy of our algorithm in comparison with two baseline algorithms.

Simplifying Complex Observation Models in Continuous POMDP Planning with Probabilistic Guarantees and Practice

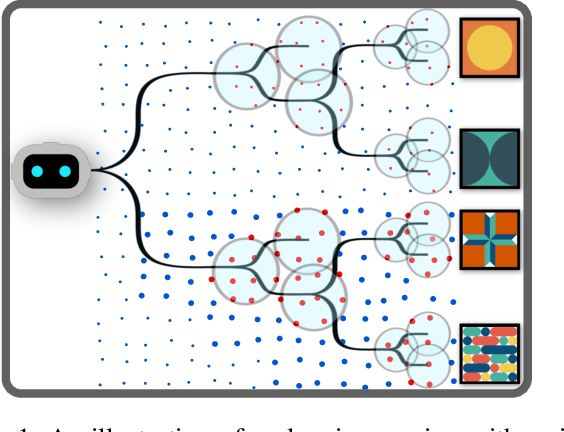
Solving partially observable Markov decision processes (POMDPs) with high dimensional and continuous observations, such as camera images, is required for many real life robotics and planning problems. Recent researches suggested machine learned probabilistic models as observation models, but their use is currently too computationally expensive for online deployment. We deal with the question of what would be the implication of using simplified observation models for planning, while retaining formal guarantees on the quality of the solution. Our main contribution is a novel probabilistic bound based on a statistical total variation distance of the simplified model. We show that it bounds the theoretical POMDP value w.r.t. original model, from the empirical planned value with the simplified model, by generalizing recent results of particle-belief MDP concentration bounds. Our calculations can be separated into offline and online parts, and we arrive at formal guarantees without having to access the costly model at all during planning, which is also a novel result. Finally, we demonstrate in simulation how to integrate the bound into the routine of an existing continuous online POMDP solver.

No Compromise in Solution Quality: Speeding Up Belief-dependent Continuous POMDPs via Adaptive Multilevel Simplification

Continuous POMDPs with general belief-dependent rewards are notoriously difficult to solve online. In this paper, we present a complete provable theory of adaptive multilevel simplification for the setting of a given externally constructed belief tree and MCTS that constructs the belief tree on the fly using an exploration technique. Our theory allows to accelerate POMDP planning with belief-dependent rewards without any sacrifice in the quality of the obtained solution. We rigorously prove each theoretical claim in the proposed unified theory. Using the general theoretical results, we present three algorithms to accelerate continuous POMDP online planning with belief-dependent rewards. Our two algorithms, SITH-BSP and LAZY-SITH-BSP, can be utilized on top of any method that constructs a belief tree externally. The third algorithm, SITH-PFT, is an anytime MCTS method that permits to plug-in any exploration technique. All our methods are guaranteed to return exactly the same optimal action as their unsimplified equivalents. We replace the costly computation of information-theoretic rewards with novel adaptive upper and lower bounds which we derive in this paper, and are of independent interest. We show that they are easy to calculate and can be tightened by the demand of our algorithms. Our approach is general; namely, any bounds that monotonically converge to the reward can be easily plugged-in to achieve significant speedup without any loss in performance. Our theory and algorithms support the challenging setting of continuous states, actions, and observations. The beliefs can be parametric or general and represented by weighted particles. We demonstrate in simulation a significant speedup in planning compared to baseline approaches with guaranteed identical performance.

Online POMDP Planning with Anytime Deterministic Guarantees

Autonomous agents operating in real-world scenarios frequently encounter uncertainty and make decisions based on incomplete information. Planning under uncertainty can be mathematically formalized using partially observable Markov decision processes (POMDPs). However, finding an optimal plan for POMDPs can be computationally expensive and is feasible only for small tasks. In recent years, approximate algorithms, such as tree search and sample-based methodologies, have emerged as state-of-the-art POMDP solvers for larger problems. Despite their effectiveness, these algorithms offer only probabilistic and often asymptotic guarantees toward the optimal solution due to their dependence on sampling. To address these limitations, we derive a deterministic relationship between a simplified solution that is easier to obtain and the theoretically optimal one. First, we derive bounds for selecting a subset of the observations to branch from while computing a complete belief at each posterior node. Then, since a complete belief update may be computationally demanding, we extend the bounds to support reduction of both the state and the observation spaces. We demonstrate how our guarantees can be integrated with existing state-of-the-art solvers that sample a subset of states and observations. As a result, the returned solution holds deterministic bounds relative to the optimal policy. Lastly, we substantiate our findings with supporting experimental results.

Measurement Simplification in ρ-POMDP with Performance Guarantees

Decision making under uncertainty is at the heart of any autonomous system acting with imperfect information. The cost of solving the decision making problem is exponential in the action and observation spaces, thus rendering it unfeasible for many online systems. This paper introduces a novel approach to efficient decision-making, by partitioning the high-dimensional observation space. Using the partitioned observation space, we formulate analytical bounds on the expected information-theoretic reward, for general belief distributions. These bounds are then used to plan efficiently while keeping performance guarantees. We show that the bounds are adaptive, computationally efficient, and that they converge to the original solution. We extend the partitioning paradigm and present a hierarchy of partitioned spaces that allows greater efficiency in planning. We then propose a specific variant of these bounds for Gaussian beliefs and show a theoretical performance improvement of at least a factor of 4. Finally, we compare our novel method to other state of the art algorithms in active SLAM scenarios, in simulation and in real experiments. In both cases we show a significant speed-up in planning with performance guarantees.