A Slices Perspective for Incremental Nonparametric Inference in High Dimensional State Spaces

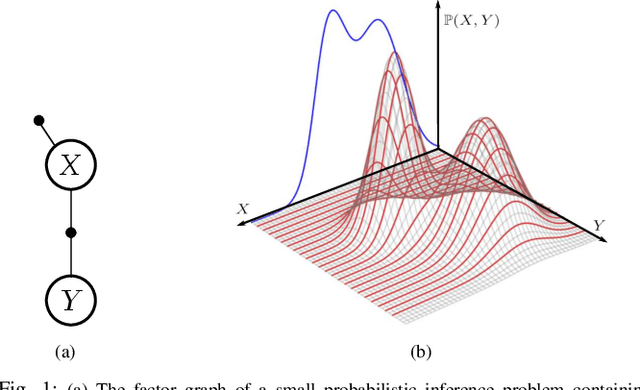
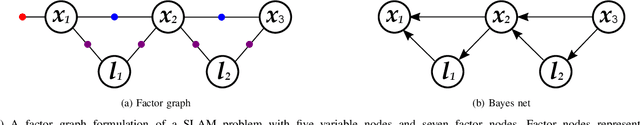
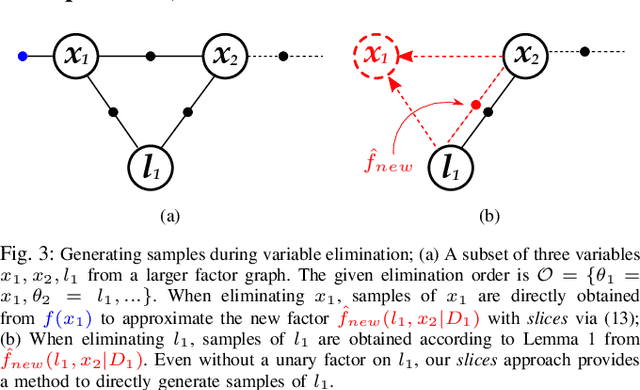
We introduce an innovative method for incremental nonparametric probabilistic inference in high-dimensional state spaces. Our approach leverages \slices from high-dimensional surfaces to efficiently approximate posterior distributions of any shape. Unlike many existing graph-based methods, our \slices perspective eliminates the need for additional intermediate reconstructions, maintaining a more accurate representation of posterior distributions. Additionally, we propose a novel heuristic to balance between accuracy and efficiency, enabling real-time operation in nonparametric scenarios. In empirical evaluations on synthetic and real-world datasets, our \slices approach consistently outperforms other state-of-the-art methods. It demonstrates superior accuracy and achieves a significant reduction in computational complexity, often by an order of magnitude.

Monte Carlo Planning in Hybrid Belief POMDPs

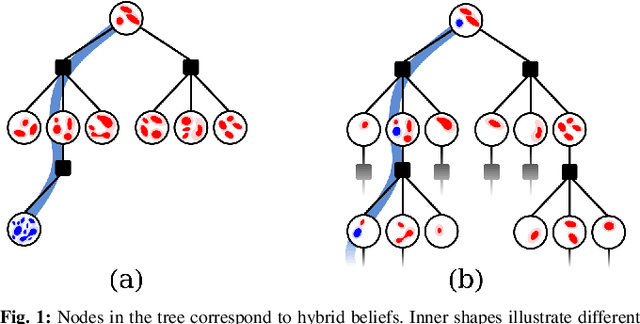
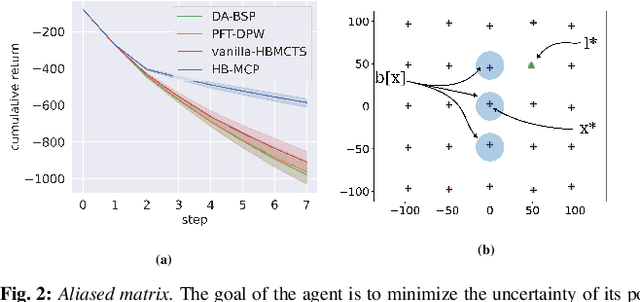
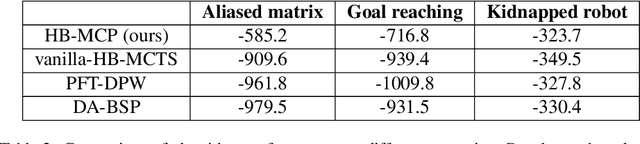
Real-world problems often require reasoning about hybrid beliefs, over both discrete and continuous random variables. Yet, such a setting has hardly been investigated in the context of planning. Moreover, existing online Partially Observable Markov Decision Processes (POMDPs) solvers do not support hybrid beliefs directly. In particular, these solvers do not address the added computational burden due to an increasing number of hypotheses with the planning horizon, which can grow exponentially. As part of this work, we present a novel algorithm, Hybrid Belief Monte Carlo Planning (HB-MCP) that utilizes the Monte Carlo Tree Search (MCTS) algorithm to solve a POMDP while maintaining a hybrid belief. We illustrate how the upper confidence bound (UCB) exploration bonus can be leveraged to guide the growth of hypotheses trees alongside the belief trees. We then evaluate our approach in highly aliased simulated environments where unresolved data association leads to multi-modal belief hypotheses.

Nonmyopic Distilled Data Association Belief Space Planning Under Budget Constraints

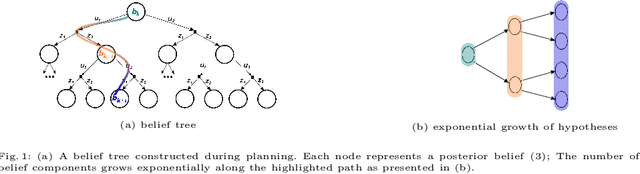
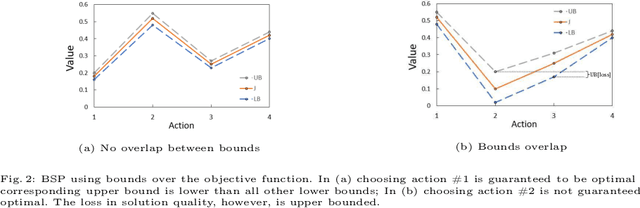
Autonomous agents operating in perceptually aliased environments should ideally be able to solve the data association problem. Yet, planning for future actions while considering this problem is not trivial. State of the art approaches therefore use multi-modal hypotheses to represent the states of the agent and of the environment. However, explicitly considering all possible data associations, the number of hypotheses grows exponentially with the planning horizon. As such, the corresponding Belief Space Planning problem quickly becomes unsolvable. Moreover, under hard computational budget constraints, some non-negligible hypotheses must eventually be pruned in both planning and inference. Nevertheless, the two processes are generally treated separately and the effect of budget constraints in one process over the other was barely studied. We present a computationally efficient method to solve the nonmyopic Belief Space Planning problem while reasoning about data association. Moreover, we rigorously analyze the effects of budget constraints in both inference and planning.

D2A-BSP: Distilled Data Association Belief Space Planning with Performance Guarantees Under Budget Constraints

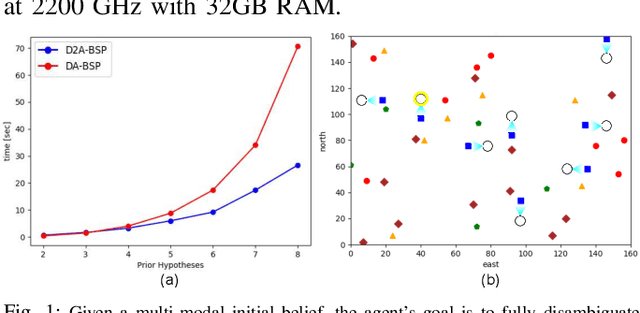
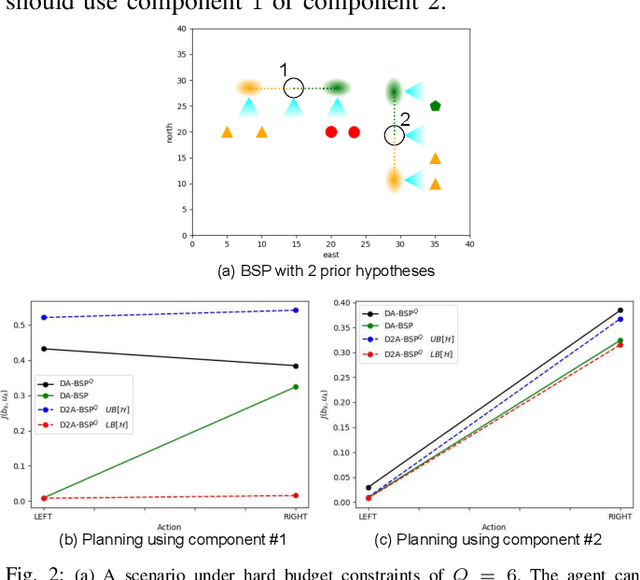
Unresolved data association in ambiguous and perceptually aliased environments leads to multi-modal hypotheses on both the robot's and the environment state. To avoid catastrophic results, when operating in such ambiguous environments, it is crucial to reason about data association within Belief Space Planning (BSP). However, explicitly considering all possible data associations, the number of hypotheses grows exponentially with the planning horizon and determining the optimal action sequence quickly becomes intractable. Moreover, with hard budget constraints where some non-negligible hypotheses must be pruned, achieving performance guarantees is crucial. In this work we present a computationally efficient novel approach that utilizes only a distilled subset of hypotheses to solve BSP problems while reasoning about data association. Furthermore, to provide performance guarantees, we derive error bounds with respect to the optimal solution. We then demonstrate our approach in an extremely aliased environment, where we manage to significantly reduce computation time without compromising on the quality of the solution.