Value Gradients with Action Adaptive Search Trees in Continuous (PO)MDPs

Solving Partially Observable Markov Decision Processes (POMDPs) in continuous state, action and observation spaces is key for autonomous planning in many real-world mobility and robotics applications. Current approaches are mostly sample based, and cannot hope to reach near-optimal solutions in reasonable time. We propose two complementary theoretical contributions. First, we formulate a novel Multiple Importance Sampling (MIS) tree for value estimation, that allows to share value information between sibling action branches. The novel MIS tree supports action updates during search time, such as gradient-based updates. Second, we propose a novel methodology to compute value gradients with online sampling based on transition likelihoods. It is applicable to MDPs, and we extend it to POMDPs via particle beliefs with the application of the propagated belief trick. The gradient estimator is computed in practice using the MIS tree with efficient Monte Carlo sampling. These two parts are combined into a new planning algorithm Action Gradient Monte Carlo Tree Search (AGMCTS). We demonstrate in a simulated environment its applicability, advantages over continuous online POMDP solvers that rely solely on sampling, and we discuss further implications.

Anytime Incremental $ρ$POMDP Planning in Continuous Spaces

Partially Observable Markov Decision Processes (POMDPs) provide a robust framework for decision-making under uncertainty in applications such as autonomous driving and robotic exploration. Their extension, $\rho$POMDPs, introduces belief-dependent rewards, enabling explicit reasoning about uncertainty. Existing online $\rho$POMDP solvers for continuous spaces rely on fixed belief representations, limiting adaptability and refinement - critical for tasks such as information-gathering. We present $\rho$POMCPOW, an anytime solver that dynamically refines belief representations, with formal guarantees of improvement over time. To mitigate the high computational cost of updating belief-dependent rewards, we propose a novel incremental computation approach. We demonstrate its effectiveness for common entropy estimators, reducing computational cost by orders of magnitude. Experimental results show that $\rho$POMCPOW outperforms state-of-the-art solvers in both efficiency and solution quality.

Simplifying Complex Observation Models in Continuous POMDP Planning with Probabilistic Guarantees and Practice

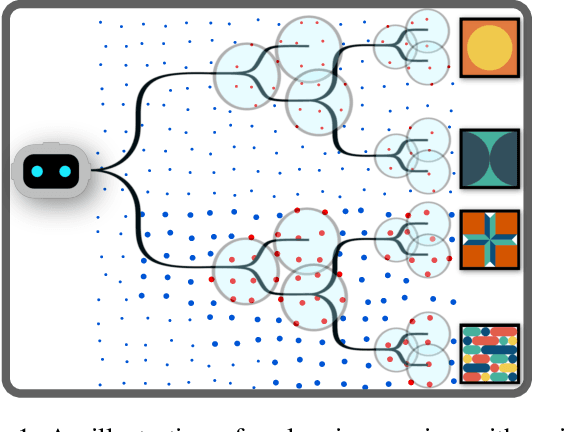
Solving partially observable Markov decision processes (POMDPs) with high dimensional and continuous observations, such as camera images, is required for many real life robotics and planning problems. Recent researches suggested machine learned probabilistic models as observation models, but their use is currently too computationally expensive for online deployment. We deal with the question of what would be the implication of using simplified observation models for planning, while retaining formal guarantees on the quality of the solution. Our main contribution is a novel probabilistic bound based on a statistical total variation distance of the simplified model. We show that it bounds the theoretical POMDP value w.r.t. original model, from the empirical planned value with the simplified model, by generalizing recent results of particle-belief MDP concentration bounds. Our calculations can be separated into offline and online parts, and we arrive at formal guarantees without having to access the costly model at all during planning, which is also a novel result. Finally, we demonstrate in simulation how to integrate the bound into the routine of an existing continuous online POMDP solver.

Data Association Aware POMDP Planning with Hypothesis Pruning Performance Guarantees

Autonomous agents that operate in the real world must often deal with partial observability, which is commonly modeled as partially observable Markov decision processes (POMDPs). However, traditional POMDP models rely on the assumption of complete knowledge of the observation source, known as fully observable data association. To address this limitation, we propose a planning algorithm that maintains multiple data association hypotheses, represented as a belief mixture, where each component corresponds to a different data association hypothesis. However, this method can lead to an exponential growth in the number of hypotheses, resulting in significant computational overhead. To overcome this challenge, we introduce a pruning-based approach for planning with ambiguous data associations. Our key contribution is to derive bounds between the value function based on the complete set of hypotheses and the value function based on a pruned-subset of the hypotheses, enabling us to establish a trade-off between computational efficiency and performance. We demonstrate how these bounds can both be used to certify any pruning heuristic in retrospect and propose a novel approach to determine which hypotheses to prune in order to ensure a predefined limit on the loss. We evaluate our approach in simulated environments and demonstrate its efficacy in handling multi-modal belief hypotheses with ambiguous data associations.