Anytime Incremental $ρ$POMDP Planning in Continuous Spaces

Partially Observable Markov Decision Processes (POMDPs) provide a robust framework for decision-making under uncertainty in applications such as autonomous driving and robotic exploration. Their extension, $\rho$POMDPs, introduces belief-dependent rewards, enabling explicit reasoning about uncertainty. Existing online $\rho$POMDP solvers for continuous spaces rely on fixed belief representations, limiting adaptability and refinement - critical for tasks such as information-gathering. We present $\rho$POMCPOW, an anytime solver that dynamically refines belief representations, with formal guarantees of improvement over time. To mitigate the high computational cost of updating belief-dependent rewards, we propose a novel incremental computation approach. We demonstrate its effectiveness for common entropy estimators, reducing computational cost by orders of magnitude. Experimental results show that $\rho$POMCPOW outperforms state-of-the-art solvers in both efficiency and solution quality.

Anytime Probabilistically Constrained Provably Convergent Online Belief Space Planning

Taking into account future risk is essential for an autonomously operating robot to find online not only the best but also a safe action to execute. In this paper, we build upon the recently introduced formulation of probabilistic belief-dependent constraints. We present an anytime approach employing the Monte Carlo Tree Search (MCTS) method in continuous domains. Unlike previous approaches, our method assures safety anytime with respect to the currently expanded search tree without relying on the convergence of the search. We prove convergence in probability with an exponential rate of a version of our algorithms and study proposed techniques via extensive simulations. Even with a tiny number of tree queries, the best action found by our approach is much safer than the baseline. Moreover, our approach constantly finds better than the baseline action in terms of objective. This is because we revise the values and statistics maintained in the search tree and remove from them the contribution of the pruned actions.

No Compromise in Solution Quality: Speeding Up Belief-dependent Continuous POMDPs via Adaptive Multilevel Simplification

Continuous POMDPs with general belief-dependent rewards are notoriously difficult to solve online. In this paper, we present a complete provable theory of adaptive multilevel simplification for the setting of a given externally constructed belief tree and MCTS that constructs the belief tree on the fly using an exploration technique. Our theory allows to accelerate POMDP planning with belief-dependent rewards without any sacrifice in the quality of the obtained solution. We rigorously prove each theoretical claim in the proposed unified theory. Using the general theoretical results, we present three algorithms to accelerate continuous POMDP online planning with belief-dependent rewards. Our two algorithms, SITH-BSP and LAZY-SITH-BSP, can be utilized on top of any method that constructs a belief tree externally. The third algorithm, SITH-PFT, is an anytime MCTS method that permits to plug-in any exploration technique. All our methods are guaranteed to return exactly the same optimal action as their unsimplified equivalents. We replace the costly computation of information-theoretic rewards with novel adaptive upper and lower bounds which we derive in this paper, and are of independent interest. We show that they are easy to calculate and can be tightened by the demand of our algorithms. Our approach is general; namely, any bounds that monotonically converge to the reward can be easily plugged-in to achieve significant speedup without any loss in performance. Our theory and algorithms support the challenging setting of continuous states, actions, and observations. The beliefs can be parametric or general and represented by weighted particles. We demonstrate in simulation a significant speedup in planning compared to baseline approaches with guaranteed identical performance.

Simplified Continuous High Dimensional Belief Space Planning with Adaptive Probabilistic Belief-dependent Constraints

Online decision making under uncertainty in partially observable domains, also known as Belief Space Planning, is a fundamental problem in robotics and Artificial Intelligence. Due to an abundance of plausible future unravelings, calculating an optimal course of action inflicts an enormous computational burden on the agent. Moreover, in many scenarios, e.g., information gathering, it is required to introduce a belief-dependent constraint. Prompted by this demand, in this paper, we consider a recently introduced probabilistic belief-dependent constrained POMDP. We present a technique to adaptively accept or discard a candidate action sequence with respect to a probabilistic belief-dependent constraint, before expanding a complete set of future observations samples and without any loss in accuracy. Moreover, using our proposed framework, we contribute an adaptive method to find a maximal feasible return (e.g., information gain) in terms of Value at Risk for the candidate action sequence with substantial acceleration. On top of that, we introduce an adaptive simplification technique for a probabilistically constrained setting. Such an approach provably returns an identical-quality solution while dramatically accelerating online decision making. Our universal framework applies to any belief-dependent constrained continuous POMDP with parametric beliefs, as well as nonparametric beliefs represented by particles. In the context of an information-theoretic constraint, our presented framework stochastically quantifies if a cumulative information gain along the planning horizon is sufficiently significant (e.g. for, information gathering, active SLAM). We apply our method to active SLAM, a highly challenging problem of high dimensional Belief Space Planning. Extensive realistic simulations corroborate the superiority of our proposed ideas.

Risk Aware Belief-dependent Constrained POMDP Planning

Risk awareness is fundamental to an online operating agent. However, it received less attention in the challenging continuous domain under partial observability. Existing constrained POMDP algorithms are typically designed for discrete state and observation spaces. In addition, current solvers for constrained formulations do not support general belief-dependent constraints. Crucially, in the POMDP setting, risk awareness in the context of a constraint was addressed in a limited way. This paper presents a novel formulation for risk-averse belief-dependent constrained POMDP. Our probabilistic constraint is general and belief-dependent, as is the reward function. The proposed universal framework applies to a continuous domain with nonparametric beliefs represented by particles or parametric beliefs. We show that our formulation better accounts for the risk than previous approaches.

Simplified Belief-Dependent Reward MCTS Planning with Guaranteed Tree Consistency

Partially Observable Markov Decision Processes (POMDPs) are notoriously hard to solve. Most advanced state-of-the-art online solvers leverage ideas of Monte Carlo Tree Search (MCTS). These solvers rapidly converge to the most promising branches of the belief tree, avoiding the suboptimal sections. Most of these algorithms are designed to utilize straightforward access to the state reward and assume the belief-dependent reward is nothing but expectation over the state reward. Thus, they are inapplicable to a more general and essential setting of belief-dependent rewards. One example of such reward is differential entropy approximated using a set of weighted particles of the belief. Such an information-theoretic reward introduces a significant computational burden. In this paper, we embed the paradigm of simplification into the MCTS algorithm. In particular, we present Simplified Information-Theoretic Particle Filter Tree (SITH-PFT), a novel variant to the MCTS algorithm that considers information-theoretic rewards but avoids the need to calculate them completely. We replace the costly calculation of information-theoretic rewards with adaptive upper and lower bounds. These bounds are easy to calculate and tightened only by the demand of our algorithm. Crucially, we guarantee precisely the same belief tree and solution that would be obtained by MCTS, which explicitly calculates the original information-theoretic rewards. Our approach is general; namely, any converging to the reward bounds can be easily plugged-in to achieve substantial speedup without any loss in performance.

Probabilistic Loss and its Online Characterization for Simplified Decision Making Under Uncertainty

It is a long-standing objective to ease the computation burden incurred by the decision making process. Identification of this mechanism's sensitivity to simplification has tremendous ramifications. Yet, algorithms for decision making under uncertainty usually lean on approximations or heuristics without quantifying their effect. Therefore, challenging scenarios could severely impair the performance of such methods. In this paper, we extend the decision making mechanism to the whole by removing standard approximations and considering all previously suppressed stochastic sources of variability. On top of this extension, our key contribution is a novel framework to simplify decision making while assessing and controlling online the simplification's impact. Furthermore, we present novel stochastic bounds on the return and characterize online the effect of simplification using this framework on a particular simplification technique - reducing the number of samples in belief representation for planning. Finally, we verify the advantages of our approach through extensive simulations.

Topology of deep neural networks

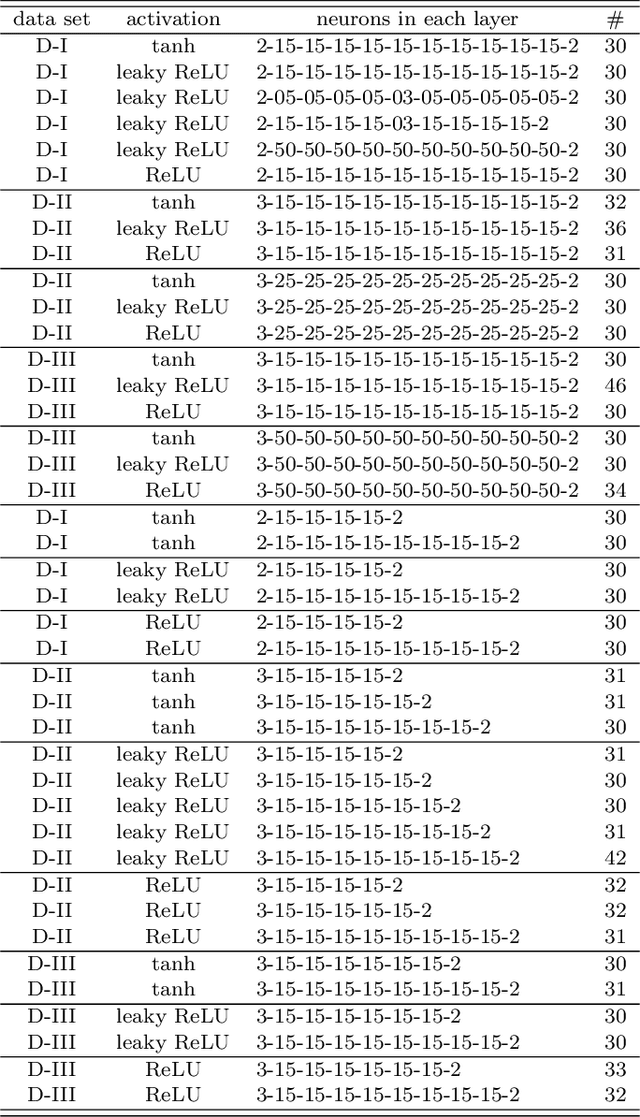
We study how the topology of a data set $M = M_a \cup M_b \subseteq \mathbb{R}^d$, representing two classes $a$ and $b$ in a binary classification problem, changes as it passes through the layers of a well-trained neural network, i.e., with perfect accuracy on training set and near-zero generalization error ($\approx 0.01\%$). The goal is to shed light on two mysteries in deep neural networks: (i) a nonsmooth activation function like ReLU outperforms a smooth one like hyperbolic tangent; (ii) successful neural network architectures rely on having many layers, even though a shallow network can approximate any function arbitrary well. We performed extensive experiments on the persistent homology of a wide range of point cloud data sets, both real and simulated. The results consistently demonstrate the following: (1) Neural networks operate by changing topology, transforming a topologically complicated data set into a topologically simple one as it passes through the layers. No matter how complicated the topology of $M$ we begin with, when passed through a well-trained neural network $f : \mathbb{R}^d \to \mathbb{R}^p$, there is a vast reduction in the Betti numbers of both components $M_a$ and $M_b$; in fact they nearly always reduce to their lowest possible values: $\beta_k\bigl(f(M_i)\bigr) = 0$ for $k \ge 1$ and $\beta_0\bigl(f(M_i)\bigr) = 1$, $i =a, b$. Furthermore, (2) the reduction in Betti numbers is significantly faster for ReLU activation than hyperbolic tangent activation as the former defines nonhomeomorphic maps that change topology, whereas the latter defines homeomorphic maps that preserve topology. Lastly, (3) shallow and deep networks transform data sets differently -- a shallow network operates mainly through changing geometry and changes topology only in its final layers, a deep one spreads topological changes more evenly across all layers.