Restricted Strong Convexity of Deep Learning Models with Smooth Activations
Paper and Code
Sep 29, 2022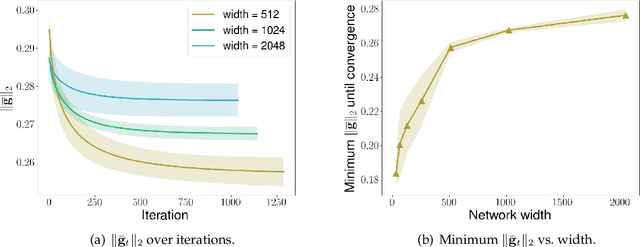
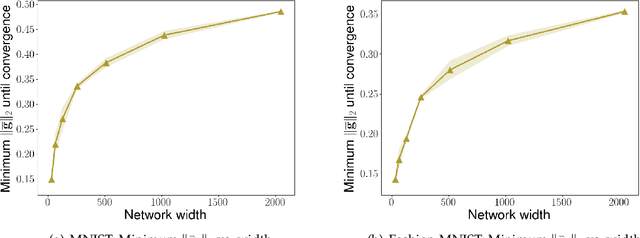
We consider the problem of optimization of deep learning models with smooth activation functions. While there exist influential results on the problem from the ``near initialization'' perspective, we shed considerable new light on the problem. In particular, we make two key technical contributions for such models with $L$ layers, $m$ width, and $\sigma_0^2$ initialization variance. First, for suitable $\sigma_0^2$, we establish a $O(\frac{\text{poly}(L)}{\sqrt{m}})$ upper bound on the spectral norm of the Hessian of such models, considerably sharpening prior results. Second, we introduce a new analysis of optimization based on Restricted Strong Convexity (RSC) which holds as long as the squared norm of the average gradient of predictors is $\Omega(\frac{\text{poly}(L)}{\sqrt{m}})$ for the square loss. We also present results for more general losses. The RSC based analysis does not need the ``near initialization" perspective and guarantees geometric convergence for gradient descent (GD). To the best of our knowledge, ours is the first result on establishing geometric convergence of GD based on RSC for deep learning models, thus becoming an alternative sufficient condition for convergence that does not depend on the widely-used Neural Tangent Kernel (NTK). We share preliminary experimental results supporting our theoretical advances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge