Loss Gradient Gaussian Width based Generalization and Optimization Guarantees

Generalization and optimization guarantees on the population loss in machine learning often rely on uniform convergence based analysis, typically based on the Rademacher complexity of the predictors. The rich representation power of modern models has led to concerns about this approach. In this paper, we present generalization and optimization guarantees in terms of the complexity of the gradients, as measured by the Loss Gradient Gaussian Width (LGGW). First, we introduce generalization guarantees directly in terms of the LGGW under a flexible gradient domination condition, which we demonstrate to hold empirically for deep models. Second, we show that sample reuse in finite sum (stochastic) optimization does not make the empirical gradient deviate from the population gradient as long as the LGGW is small. Third, focusing on deep networks, we present results showing how to bound their LGGW under mild assumptions. In particular, we show that their LGGW can be bounded (a) by the $L_2$-norm of the loss Hessian eigenvalues, which has been empirically shown to be $\tilde{O}(1)$ for commonly used deep models; and (b) in terms of the Gaussian width of the featurizer, i.e., the output of the last-but-one layer. To our knowledge, our generalization and optimization guarantees in terms of LGGW are the first results of its kind, avoid the pitfalls of predictor Rademacher complexity based analysis, and hold considerable promise towards quantitatively tight bounds for deep models.

RecMind: Large Language Model Powered Agent For Recommendation

Recent advancements in instructing Large Language Models (LLMs) to utilize external tools and execute multi-step plans have significantly enhanced their ability to solve intricate tasks, ranging from mathematical problems to creative writing. Yet, there remains a notable gap in studying the capacity of LLMs in responding to personalized queries such as a recommendation request. To bridge this gap, we have designed an LLM-powered autonomous recommender agent, RecMind, which is capable of providing precise personalized recommendations through careful planning, utilizing tools for obtaining external knowledge, and leveraging individual data. We propose a novel algorithm, Self-Inspiring, to improve the planning ability of the LLM agent. At each intermediate planning step, the LLM 'self-inspires' to consider all previously explored states to plan for next step. This mechanism greatly improves the model's ability to comprehend and utilize historical planning information for recommendation. We evaluate RecMind's performance in various recommendation scenarios, including rating prediction, sequential recommendation, direct recommendation, explanation generation, and review summarization. Our experiment shows that RecMind outperforms existing zero/few-shot LLM-based recommendation methods in different recommendation tasks and achieves competitive performance to a recent model P5, which requires fully pre-train for the recommendation tasks.

Stability Based Generalization Bounds for Exponential Family Langevin Dynamics

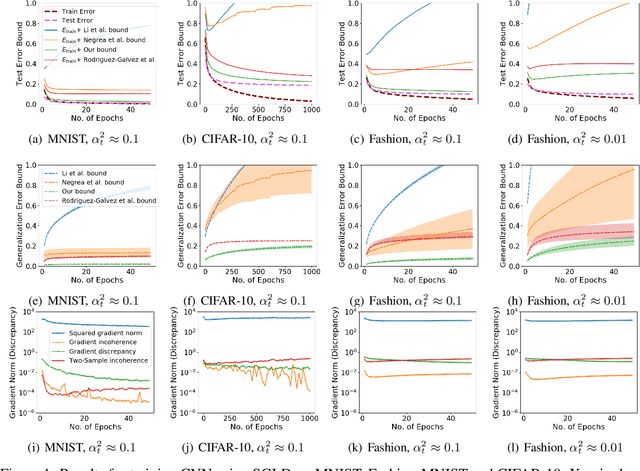
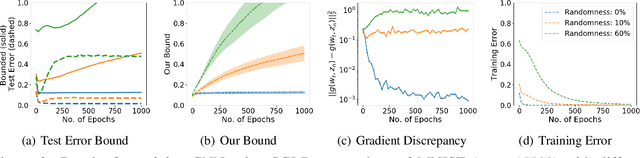
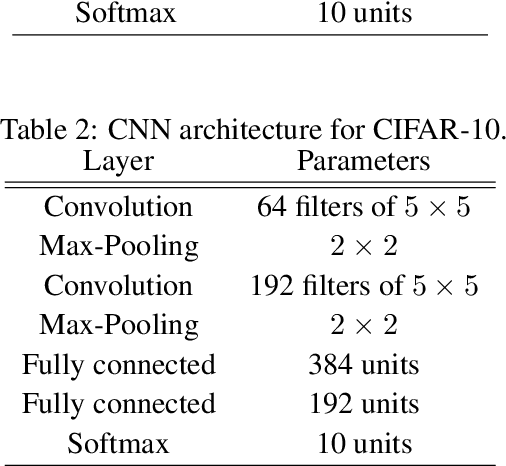
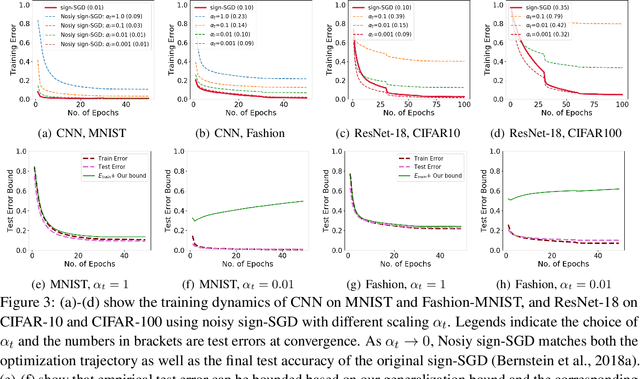
We study generalization bounds for noisy stochastic mini-batch iterative algorithms based on the notion of stability. Recent years have seen key advances in data-dependent generalization bounds for noisy iterative learning algorithms such as stochastic gradient Langevin dynamics (SGLD) based on stability (Mou et al., 2018; Li et al., 2020) and information theoretic approaches (Xu and Raginsky, 2017; Negrea et al., 2019; Steinke and Zakynthinou, 2020; Haghifam et al., 2020). In this paper, we unify and substantially generalize stability based generalization bounds and make three technical advances. First, we bound the generalization error of general noisy stochastic iterative algorithms (not necessarily gradient descent) in terms of expected (not uniform) stability. The expected stability can in turn be bounded by a Le Cam Style Divergence. Such bounds have a O(1/n) sample dependence unlike many existing bounds with O(1/\sqrt{n}) dependence. Second, we introduce Exponential Family Langevin Dynamics(EFLD) which is a substantial generalization of SGLD and which allows exponential family noise to be used with stochastic gradient descent (SGD). We establish data-dependent expected stability based generalization bounds for general EFLD algorithms. Third, we consider an important special case of EFLD: noisy sign-SGD, which extends sign-SGD using Bernoulli noise over {-1,+1}. Generalization bounds for noisy sign-SGD are implied by that of EFLD and we also establish optimization guarantees for the algorithm. Further, we present empirical results on benchmark datasets to illustrate that our bounds are non-vacuous and quantitatively much sharper than existing bounds.

Noisy Truncated SGD: Optimization and Generalization

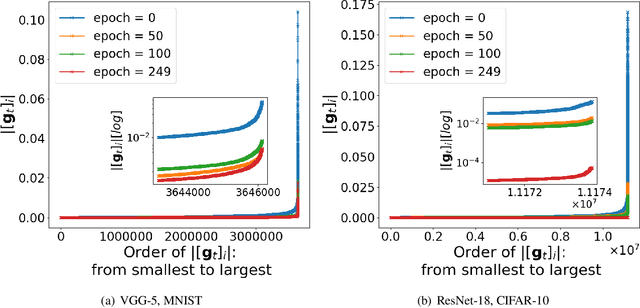
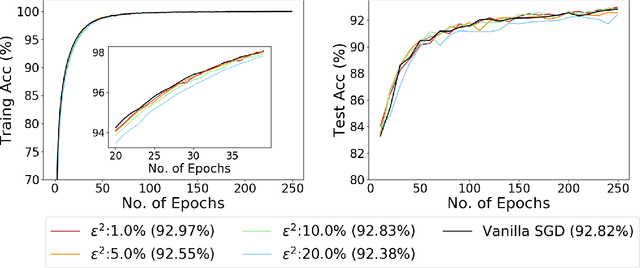
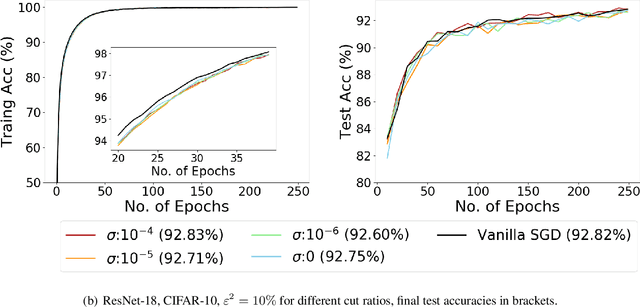
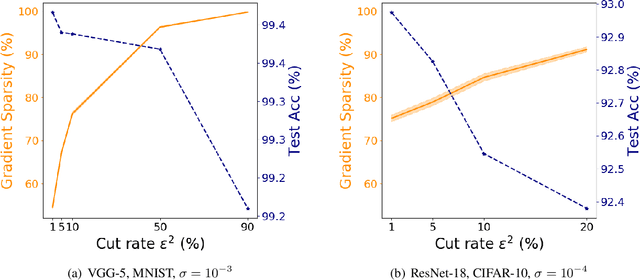
Recent empirical work on SGD applied to over-parameterized deep learning has shown that most gradient components over epochs are quite small. Inspired by such observations, we rigorously study properties of noisy truncated SGD (NT-SGD), a noisy gradient descent algorithm that truncates (hard thresholds) the majority of small gradient components to zeros and then adds Gaussian noise to all components. Considering non-convex smooth problems, we first establish the rate of convergence of NT-SGD in terms of empirical gradient norms, and show the rate to be of the same order as the vanilla SGD. Further, we prove that NT-SGD can provably escape from saddle points and requires less noise compared to previous related work. We also establish a generalization bound for NT-SGD using uniform stability based on discretized generalized Langevin dynamics. Our experiments on MNIST (VGG-5) and CIFAR-10 (ResNet-18) demonstrate that NT-SGD matches the speed and accuracy of vanilla SGD, and can successfully escape sharp minima while having better theoretical properties.

Bypassing the Ambient Dimension: Private SGD with Gradient Subspace Identification

Differentially private SGD (DP-SGD) is one of the most popular methods for solving differentially private empirical risk minimization (ERM). Due to its noisy perturbation on each gradient update, the error rate of DP-SGD scales with the ambient dimension $p$, the number of parameters in the model. Such dependence can be problematic for over-parameterized models where $p \gg n$, the number of training samples. Existing lower bounds on private ERM show that such dependence on $p$ is inevitable in the worst case. In this paper, we circumvent the dependence on the ambient dimension by leveraging a low-dimensional structure of gradient space in deep networks---that is, the stochastic gradients for deep nets usually stay in a low dimensional subspace in the training process. We propose Projected DP-SGD that performs noise reduction by projecting the noisy gradients to a low-dimensional subspace, which is given by the top gradient eigenspace on a small public dataset. We provide a general sample complexity analysis on the public dataset for the gradient subspace identification problem and demonstrate that under certain low-dimensional assumptions the public sample complexity only grows logarithmically in $p$. Finally, we provide a theoretical analysis and empirical evaluations to show that our method can substantially improve the accuracy of DP-SGD.

Private Stochastic Non-Convex Optimization: Adaptive Algorithms and Tighter Generalization Bounds

We study differentially private (DP) algorithms for stochastic non-convex optimization. In this problem, the goal is to minimize the population loss over a $p$-dimensional space given $n$ i.i.d. samples drawn from a distribution. We improve upon the population gradient bound of ${\sqrt{p}}/{\sqrt{n}}$ from prior work and obtain a sharper rate of $\sqrt[4]{p}/\sqrt{n}$. We obtain this rate by providing the first analyses on a collection of private gradient-based methods, including adaptive algorithms DP RMSProp and DP Adam. Our proof technique leverages the connection between differential privacy and adaptive data analysis to bound gradient estimation error at every iterate, which circumvents the worse generalization bound from the standard uniform convergence argument. Finally, we evaluate the proposed algorithms on two popular deep learning tasks and demonstrate the empirical advantages of DP adaptive gradient methods over standard DP SGD.

De-randomized PAC-Bayes Margin Bounds: Applications to Non-convex and Non-smooth Predictors

In spite of several notable efforts, explaining the generalization of deterministic deep nets, e.g., ReLU-nets, has remained challenging. Existing approaches usually need to bound the Lipschitz constant of such deep nets but such bounds have been shown to increase substantially with the number of training samples yielding vacuous generalization bounds [Nagarajan and Kolter, 2019a]. In this paper, we present new de-randomized PAC-Bayes margin bounds for deterministic non-convex and non-smooth predictors, e.g., ReLU-nets. The bounds depend on a trade-off between the $L_2$-norm of the weights and the effective curvature (`flatness') of the predictor, avoids any dependency on the Lipschitz constant, and yield meaningful (decreasing) bounds with increase in training set size. Our analysis first develops a de-randomization argument for non-convex but smooth predictors, e.g., linear deep networks (LDNs). We then consider non-smooth predictors which for any given input realize as a smooth predictor, e.g., ReLU-nets become some LDN for a given input, but the realized smooth predictor can be different for different inputs. For such non-smooth predictors, we introduce a new PAC-Bayes analysis that maintains distributions over the structure as well as parameters of smooth predictors, e.g., LDNs corresponding to ReLU-nets, which after de-randomization yields a bound for the deterministic non-smooth predictor. We present empirical results to illustrate the efficacy of our bounds over changing training set size and randomness in labels.

Hessian based analysis of SGD for Deep Nets: Dynamics and Generalization

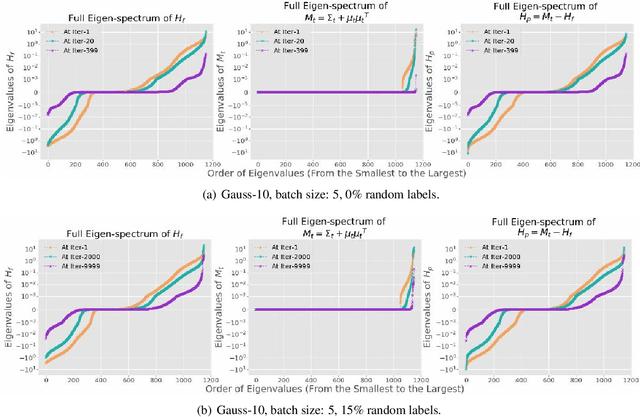
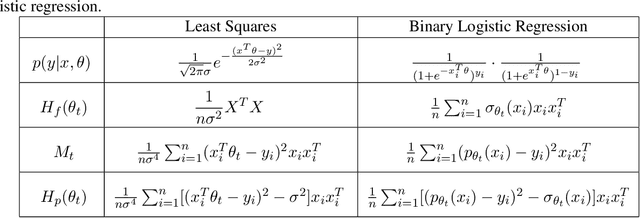
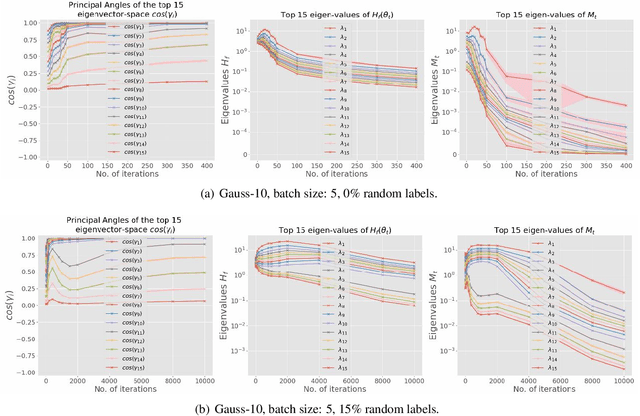
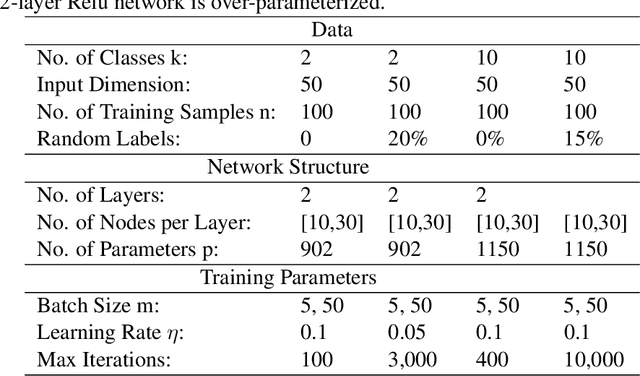
While stochastic gradient descent (SGD) and variants have been surprisingly successful for training deep nets, several aspects of the optimization dynamics and generalization are still not well understood. In this paper, we present new empirical observations and theoretical results on both the optimization dynamics and generalization behavior of SGD for deep nets based on the Hessian of the training loss and associated quantities. We consider three specific research questions: (1) what is the relationship between the Hessian of the loss and the second moment of stochastic gradients (SGs)? (2) how can we characterize the stochastic optimization dynamics of SGD with fixed and adaptive step sizes and diagonal pre-conditioning based on the first and second moments of SGs? and (3) how can we characterize a scale-invariant generalization bound of deep nets based on the Hessian of the loss, which by itself is not scale invariant? We shed light on these three questions using theoretical results supported by extensive empirical observations, with experiments on synthetic data, MNIST, and CIFAR-10, with different batch sizes, and with different difficulty levels by synthetically adding random labels.

Distributed Private Online Learning for Social Big Data Computing over Data Center Networks

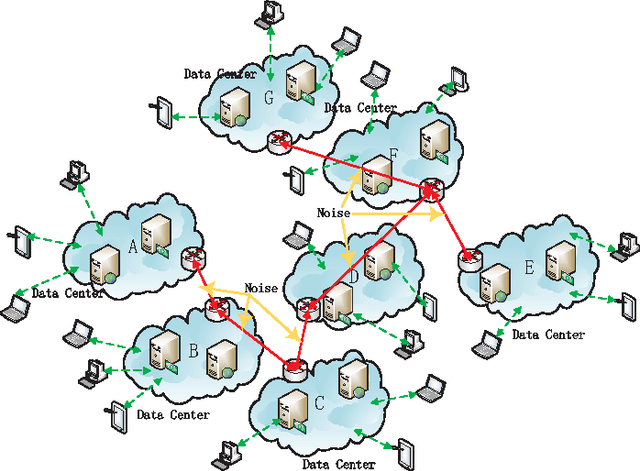
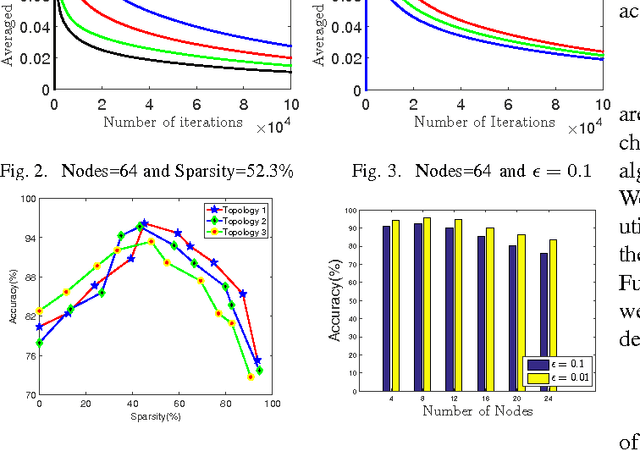
With the rapid growth of Internet technologies, cloud computing and social networks have become ubiquitous. An increasing number of people participate in social networks and massive online social data are obtained. In order to exploit knowledge from copious amounts of data obtained and predict social behavior of users, we urge to realize data mining in social networks. Almost all online websites use cloud services to effectively process the large scale of social data, which are gathered from distributed data centers. These data are so large-scale, high-dimension and widely distributed that we propose a distributed sparse online algorithm to handle them. Additionally, privacy-protection is an important point in social networks. We should not compromise the privacy of individuals in networks, while these social data are being learned for data mining. Thus we also consider the privacy problem in this article. Our simulations shows that the appropriate sparsity of data would enhance the performance of our algorithm and the privacy-preserving method does not significantly hurt the performance of the proposed algorithm.

Differentially Private Online Learning for Cloud-Based Video Recommendation with Multimedia Big Data in Social Networks

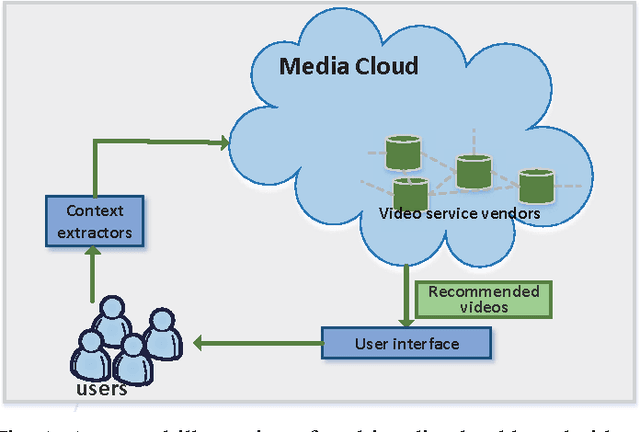
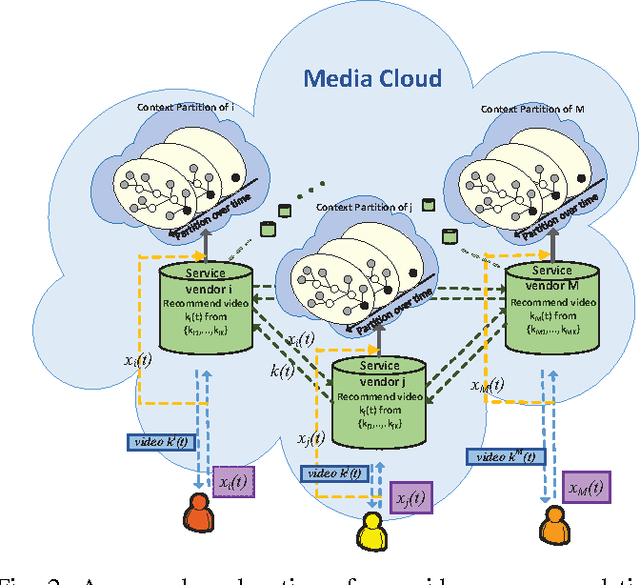
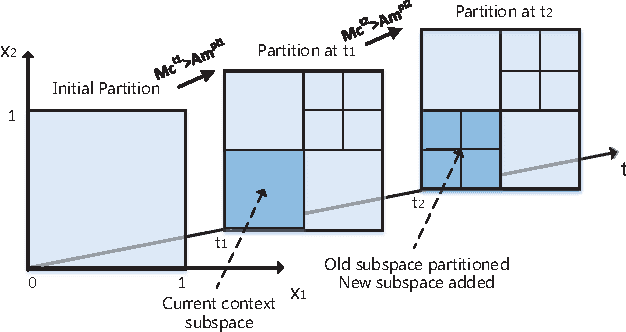
With the rapid growth in multimedia services and the enormous offers of video contents in online social networks, users have difficulty in obtaining their interests. Therefore, various personalized recommendation systems have been proposed. However, they ignore that the accelerated proliferation of social media data has led to the big data era, which has greatly impeded the process of video recommendation. In addition, none of them has considered both the privacy of users' contexts (e,g., social status, ages and hobbies) and video service vendors' repositories, which are extremely sensitive and of significant commercial value. To handle the problems, we propose a cloud-assisted differentially private video recommendation system based on distributed online learning. In our framework, service vendors are modeled as distributed cooperative learners, recommending videos according to user's context, while simultaneously adapting the video-selection strategy based on user-click feedback to maximize total user clicks (reward). Considering the sparsity and heterogeneity of big social media data, we also propose a novel geometric differentially private model, which can greatly reduce the performance (recommendation accuracy) loss. Our simulation shows the proposed algorithms outperform other existing methods and keep a delicate balance between computing accuracy and privacy preserving level.