DeCom: Deep Coupled-Factorization Machine for Post COVID-19 Respiratory Syncytial Virus Prediction with Nonpharmaceutical Interventions Awareness

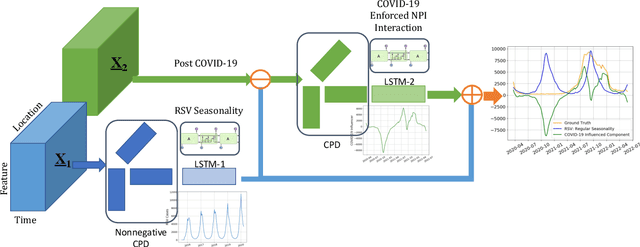
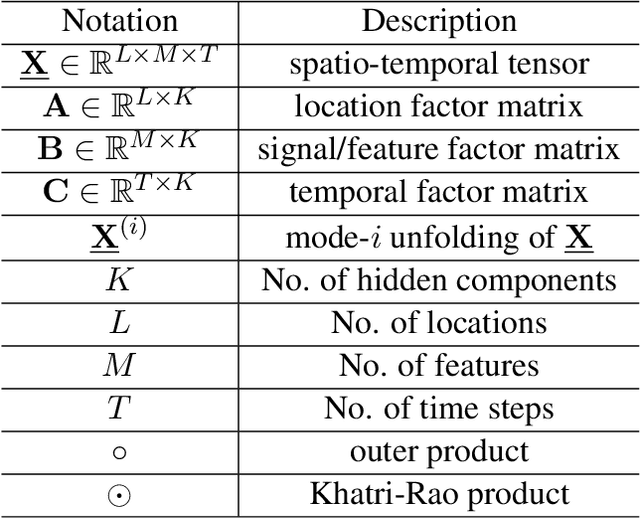
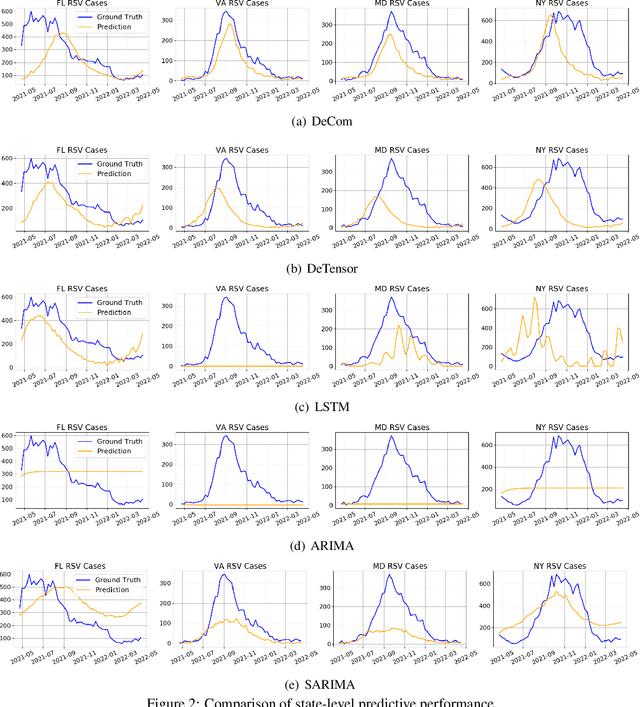
Respiratory syncytial virus (RSV) is one of the most dangerous respiratory diseases for infants and young children. Due to the nonpharmaceutical intervention (NPI) imposed in the COVID-19 outbreak, the seasonal transmission pattern of RSV has been discontinued in 2020 and then shifted months ahead in 2021 in the northern hemisphere. It is critical to understand how COVID-19 impacts RSV and build predictive algorithms to forecast the timing and intensity of RSV reemergence in post-COVID-19 seasons. In this paper, we propose a deep coupled tensor factorization machine, dubbed as DeCom, for post COVID-19 RSV prediction. DeCom leverages tensor factorization and residual modeling. It enables us to learn the disrupted RSV transmission reliably under COVID-19 by taking both the regular seasonal RSV transmission pattern and the NPI into consideration. Experimental results on a real RSV dataset show that DeCom is more accurate than the state-of-the-art RSV prediction algorithms and achieves up to 46% lower root mean square error and 49% lower mean absolute error for country-level prediction compared to the baselines.

"Nice to meet you!": Expressing Emotions with Movement Gestures and Textual Content in Automatic Handwriting Robots

Text-writing robots have been used in assistive writing and drawing applications. However, robots do not convey emotional tones in the writing process due to the lack of behaviors humans typically adopt. To examine how people interpret designed robotic expressions of emotion through both movements and textual output, we used a pen-plotting robot to generate texts by performing human-like behaviors like stop-and-go, speed, and pressure variation. We examined how people convey emotion in the writing process by observing how they wrote in different emotional contexts. We then mapped these human expressions during writing to the handwriting robot and measured how well other participants understood the robot's affective expression. We found that textual output was the strongest determinant of participants' ability to perceive the robot's emotions, whereas parameters of gestural movements of the robots like speed, fluency, pressure, size, and acceleration could be useful for understanding the context of the writing expression.

Stability Based Generalization Bounds for Exponential Family Langevin Dynamics

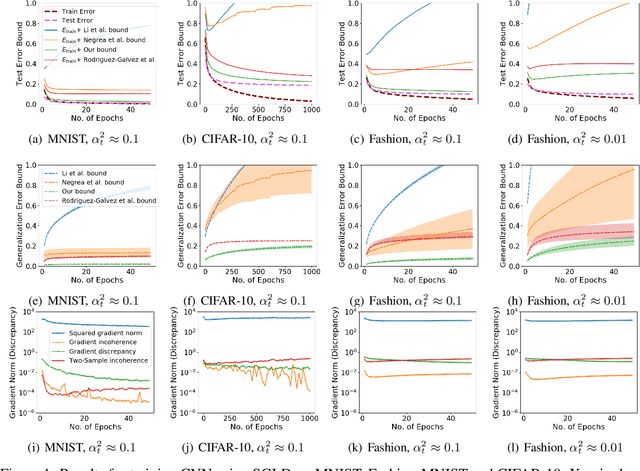
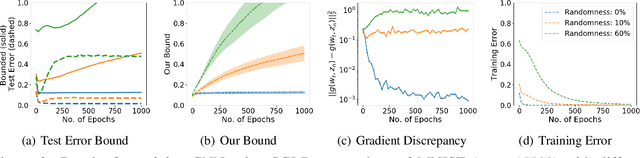
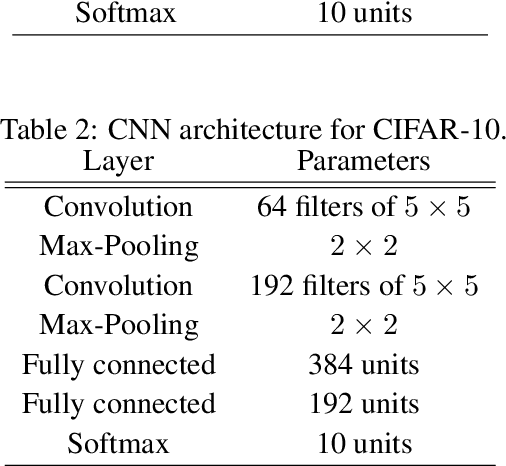
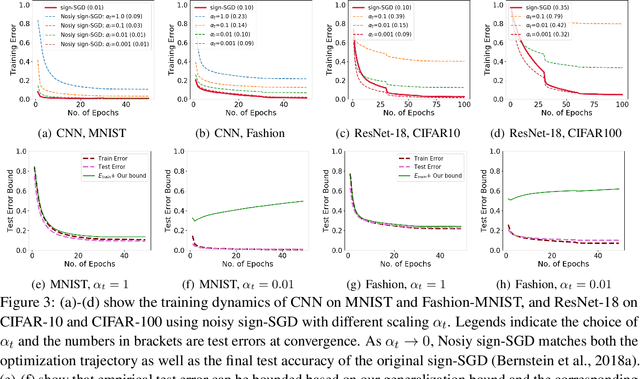
We study generalization bounds for noisy stochastic mini-batch iterative algorithms based on the notion of stability. Recent years have seen key advances in data-dependent generalization bounds for noisy iterative learning algorithms such as stochastic gradient Langevin dynamics (SGLD) based on stability (Mou et al., 2018; Li et al., 2020) and information theoretic approaches (Xu and Raginsky, 2017; Negrea et al., 2019; Steinke and Zakynthinou, 2020; Haghifam et al., 2020). In this paper, we unify and substantially generalize stability based generalization bounds and make three technical advances. First, we bound the generalization error of general noisy stochastic iterative algorithms (not necessarily gradient descent) in terms of expected (not uniform) stability. The expected stability can in turn be bounded by a Le Cam Style Divergence. Such bounds have a O(1/n) sample dependence unlike many existing bounds with O(1/\sqrt{n}) dependence. Second, we introduce Exponential Family Langevin Dynamics(EFLD) which is a substantial generalization of SGLD and which allows exponential family noise to be used with stochastic gradient descent (SGD). We establish data-dependent expected stability based generalization bounds for general EFLD algorithms. Third, we consider an important special case of EFLD: noisy sign-SGD, which extends sign-SGD using Bernoulli noise over {-1,+1}. Generalization bounds for noisy sign-SGD are implied by that of EFLD and we also establish optimization guarantees for the algorithm. Further, we present empirical results on benchmark datasets to illustrate that our bounds are non-vacuous and quantitatively much sharper than existing bounds.

Learning and Dynamical Models for Sub-seasonal Climate Forecasting: Comparison and Collaboration

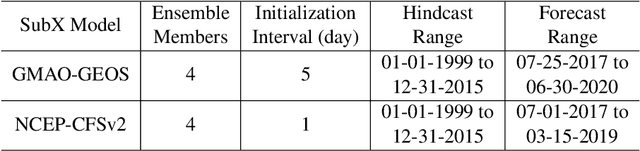
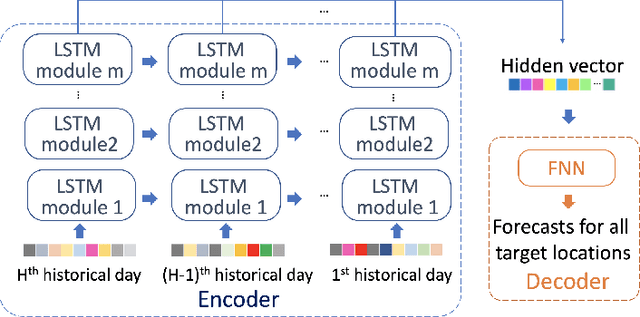
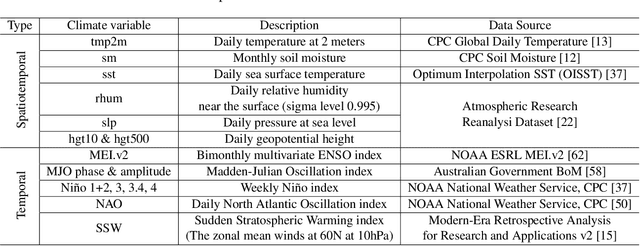
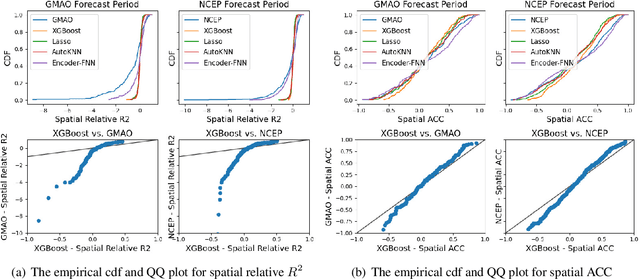
Sub-seasonal climate forecasting (SSF) is the prediction of key climate variables such as temperature and precipitation on the 2-week to 2-month time horizon. Skillful SSF would have substantial societal value in areas such as agricultural productivity, hydrology and water resource management, and emergency planning for extreme events such as droughts and wildfires. Despite its societal importance, SSF has stayed a challenging problem compared to both short-term weather forecasting and long-term seasonal forecasting. Recent studies have shown the potential of machine learning (ML) models to advance SSF. In this paper, for the first time, we perform a fine-grained comparison of a suite of modern ML models with start-of-the-art physics-based dynamical models from the Subseasonal Experiment (SubX) project for SSF in the western contiguous United States. Additionally, we explore mechanisms to enhance the ML models by using forecasts from dynamical models. Empirical results illustrate that, on average, ML models outperform dynamical models while the ML models tend to be conservatives in their forecasts compared to the SubX models. Further, we illustrate that ML models make forecasting errors under extreme weather conditions, e.g., cold waves due to the polar vortex, highlighting the need for separate models for extreme events. Finally, we show that suitably incorporating dynamical model forecasts as inputs to ML models can substantially improve the forecasting performance of the ML models. The SSF dataset constructed for the work, dynamical model predictions, and code for the ML models are released along with the paper for the benefit of the broader machine learning community.

Noisy Truncated SGD: Optimization and Generalization

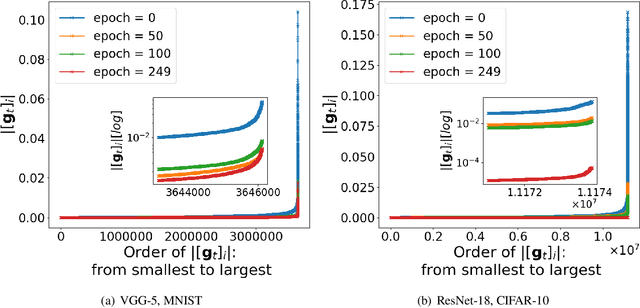
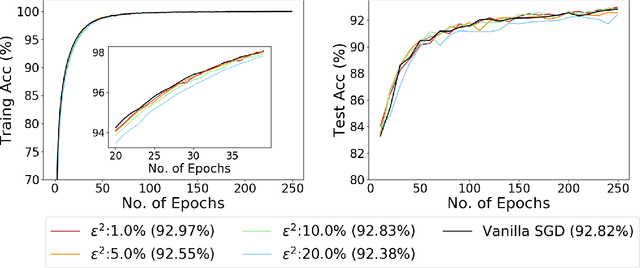
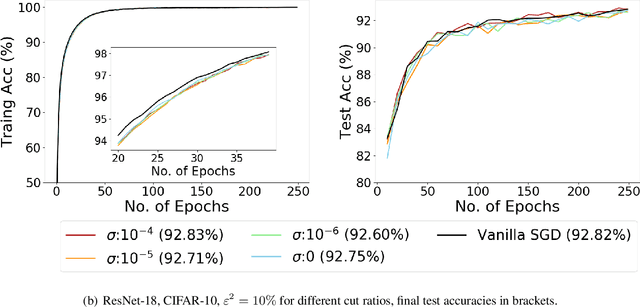
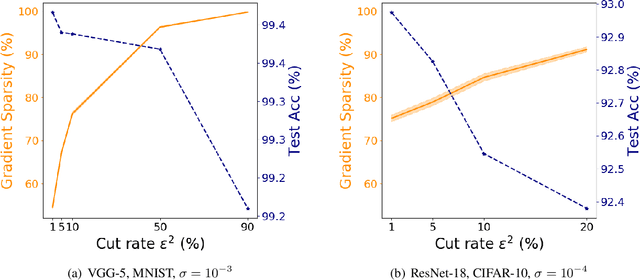
Recent empirical work on SGD applied to over-parameterized deep learning has shown that most gradient components over epochs are quite small. Inspired by such observations, we rigorously study properties of noisy truncated SGD (NT-SGD), a noisy gradient descent algorithm that truncates (hard thresholds) the majority of small gradient components to zeros and then adds Gaussian noise to all components. Considering non-convex smooth problems, we first establish the rate of convergence of NT-SGD in terms of empirical gradient norms, and show the rate to be of the same order as the vanilla SGD. Further, we prove that NT-SGD can provably escape from saddle points and requires less noise compared to previous related work. We also establish a generalization bound for NT-SGD using uniform stability based on discretized generalized Langevin dynamics. Our experiments on MNIST (VGG-5) and CIFAR-10 (ResNet-18) demonstrate that NT-SGD matches the speed and accuracy of vanilla SGD, and can successfully escape sharp minima while having better theoretical properties.

Experiments with Rich Regime Training for Deep Learning

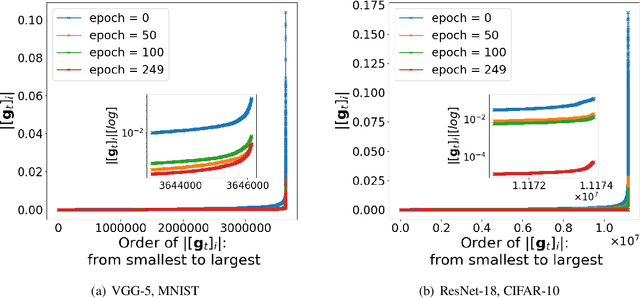
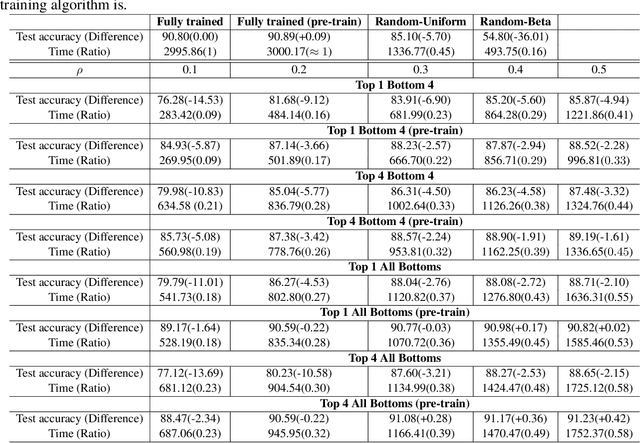
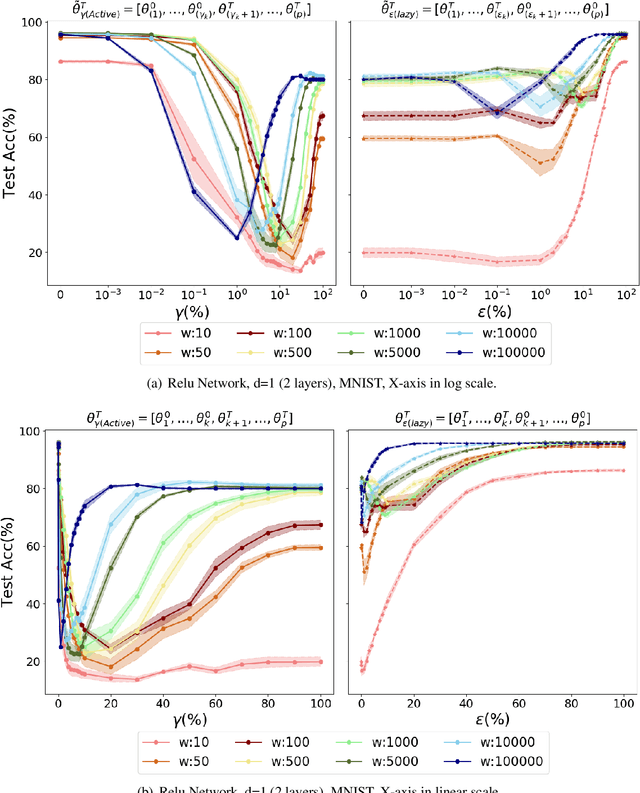
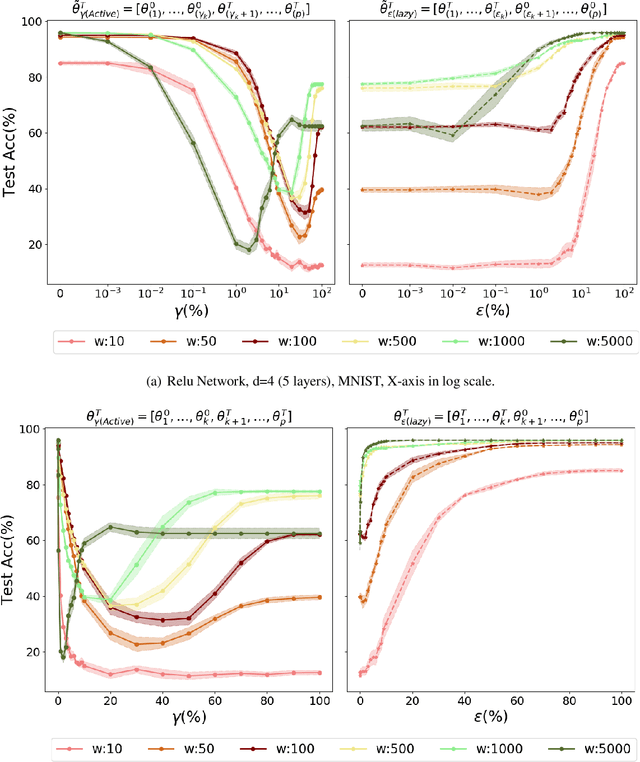
In spite of advances in understanding lazy training, recent work attributes the practical success of deep learning to the rich regime with complex inductive bias. In this paper, we study rich regime training empirically with benchmark datasets, and find that while most parameters are lazy, there is always a small number of active parameters which change quite a bit during training. We show that re-initializing (resetting to their initial random values) the active parameters leads to worse generalization. Further, we show that most of the active parameters are in the bottom layers, close to the input, especially as the networks become wider. Based on such observations, we study static Layer-Wise Sparse (LWS) SGD, which only updates some subsets of layers. We find that only updating the top and bottom layers have good generalization and, as expected, only updating the top layers yields a fast algorithm. Inspired by this, we investigate probabilistic LWS-SGD, which mostly updates the top layers and occasionally updates the full network. We show that probabilistic LWS-SGD matches the generalization performance of vanilla SGD and the back-propagation time can be 2-5 times more efficient.

Sub-Seasonal Climate Forecasting via Machine Learning: Challenges, Analysis, and Advances

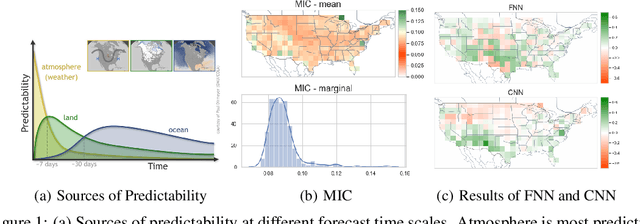
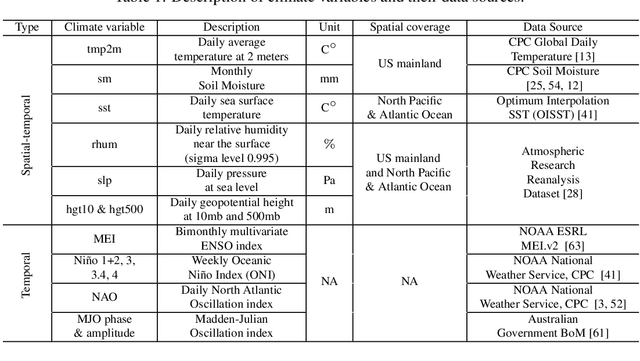
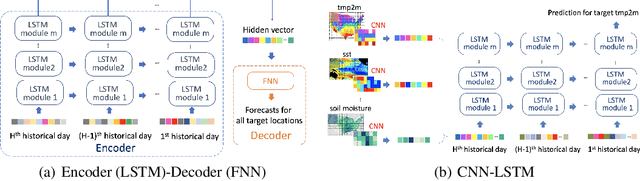
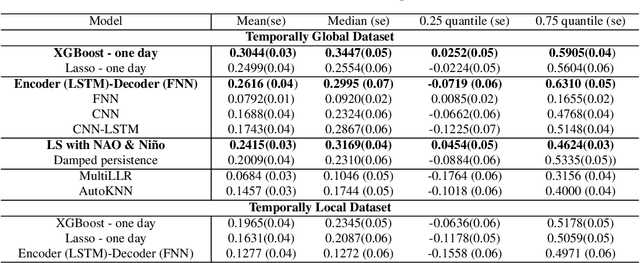
Sub-seasonal climate forecasting (SSF) focuses on predicting key climate variables such as temperature and precipitation in the 2-week to 2-month time scales. Skillful SSF would have immense societal value, in areas such as agricultural productivity, water resource management, transportation and aviation systems, and emergency planning for extreme weather events. However, SSF is considered more challenging than either weather prediction or even seasonal prediction. In this paper, we carefully study a variety of machine learning (ML) approaches for SSF over the US mainland. While atmosphere-land-ocean couplings and the limited amount of good quality data makes it hard to apply black-box ML naively, we show that with carefully constructed feature representations, even linear regression models, e.g., Lasso, can be made to perform well. Among a broad suite of 10 ML approaches considered, gradient boosting performs the best, and deep learning (DL) methods show some promise with careful architecture choices. Overall, suitable ML methods are able to outperform the climatological baseline, i.e., predictions based on the 30-year average at a given location and time. Further, based on studying feature importance, ocean (especially indices based on climatic oscillations such as El Nino) and land (soil moisture) covariates are found to be predictive, whereas atmospheric covariates are not considered helpful.

Hessian based analysis of SGD for Deep Nets: Dynamics and Generalization

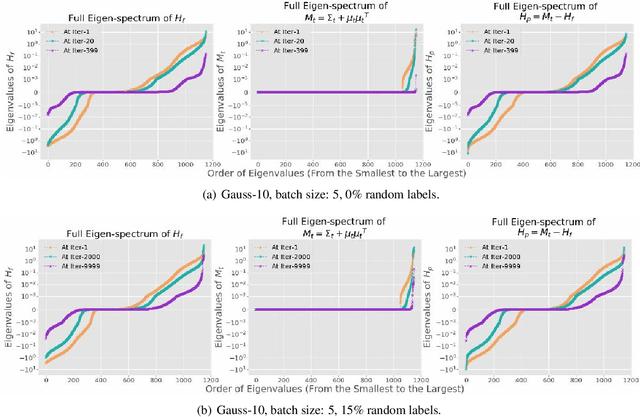
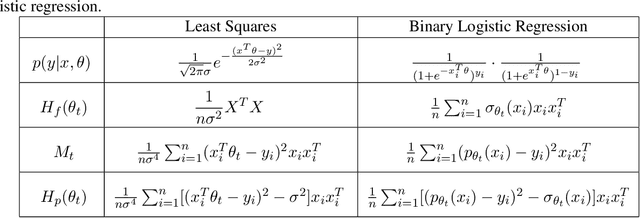
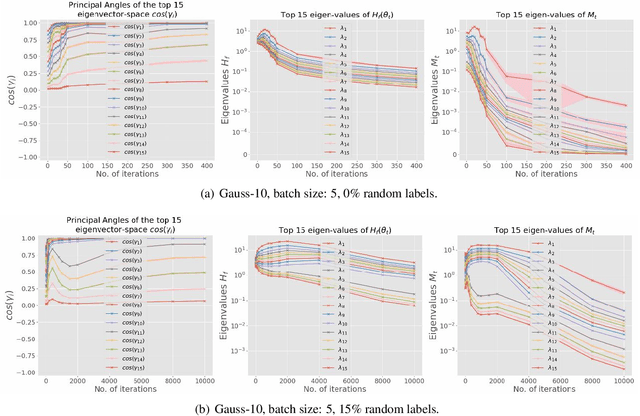
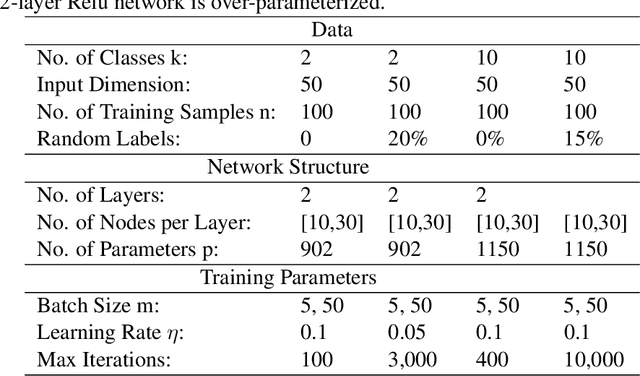
While stochastic gradient descent (SGD) and variants have been surprisingly successful for training deep nets, several aspects of the optimization dynamics and generalization are still not well understood. In this paper, we present new empirical observations and theoretical results on both the optimization dynamics and generalization behavior of SGD for deep nets based on the Hessian of the training loss and associated quantities. We consider three specific research questions: (1) what is the relationship between the Hessian of the loss and the second moment of stochastic gradients (SGs)? (2) how can we characterize the stochastic optimization dynamics of SGD with fixed and adaptive step sizes and diagonal pre-conditioning based on the first and second moments of SGs? and (3) how can we characterize a scale-invariant generalization bound of deep nets based on the Hessian of the loss, which by itself is not scale invariant? We shed light on these three questions using theoretical results supported by extensive empirical observations, with experiments on synthetic data, MNIST, and CIFAR-10, with different batch sizes, and with different difficulty levels by synthetically adding random labels.