Hessian based analysis of SGD for Deep Nets: Dynamics and Generalization

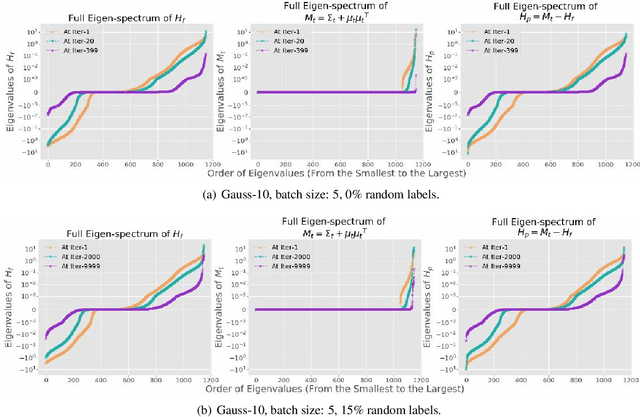
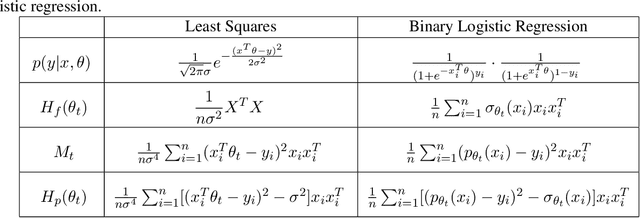
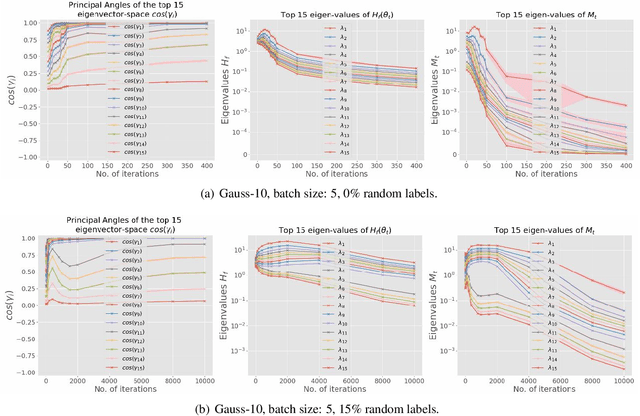
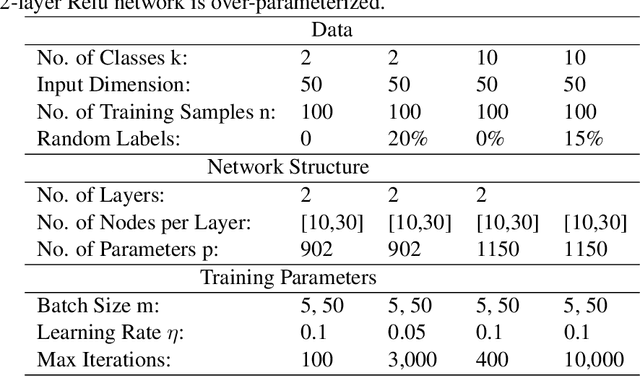
While stochastic gradient descent (SGD) and variants have been surprisingly successful for training deep nets, several aspects of the optimization dynamics and generalization are still not well understood. In this paper, we present new empirical observations and theoretical results on both the optimization dynamics and generalization behavior of SGD for deep nets based on the Hessian of the training loss and associated quantities. We consider three specific research questions: (1) what is the relationship between the Hessian of the loss and the second moment of stochastic gradients (SGs)? (2) how can we characterize the stochastic optimization dynamics of SGD with fixed and adaptive step sizes and diagonal pre-conditioning based on the first and second moments of SGs? and (3) how can we characterize a scale-invariant generalization bound of deep nets based on the Hessian of the loss, which by itself is not scale invariant? We shed light on these three questions using theoretical results supported by extensive empirical observations, with experiments on synthetic data, MNIST, and CIFAR-10, with different batch sizes, and with different difficulty levels by synthetically adding random labels.