DMPlug: A Plug-in Method for Solving Inverse Problems with Diffusion Models

Pretrained diffusion models (DMs) have recently been popularly used in solving inverse problems (IPs). The existing methods mostly interleave iterative steps in the reverse diffusion process and iterative steps to bring the iterates closer to satisfying the measurement constraint. However, such interleaving methods struggle to produce final results that look like natural objects of interest (i.e., manifold feasibility) and fit the measurement (i.e., measurement feasibility), especially for nonlinear IPs. Moreover, their capabilities to deal with noisy IPs with unknown types and levels of measurement noise are unknown. In this paper, we advocate viewing the reverse process in DMs as a function and propose a novel plug-in method for solving IPs using pretrained DMs, dubbed DMPlug. DMPlug addresses the issues of manifold feasibility and measurement feasibility in a principled manner, and also shows great potential for being robust to unknown types and levels of noise. Through extensive experiments across various IP tasks, including two linear and three nonlinear IPs, we demonstrate that DMPlug consistently outperforms state-of-the-art methods, often by large margins especially for nonlinear IPs. The code is available at https://github.com/sun-umn/DMPlug.

Stability Based Generalization Bounds for Exponential Family Langevin Dynamics

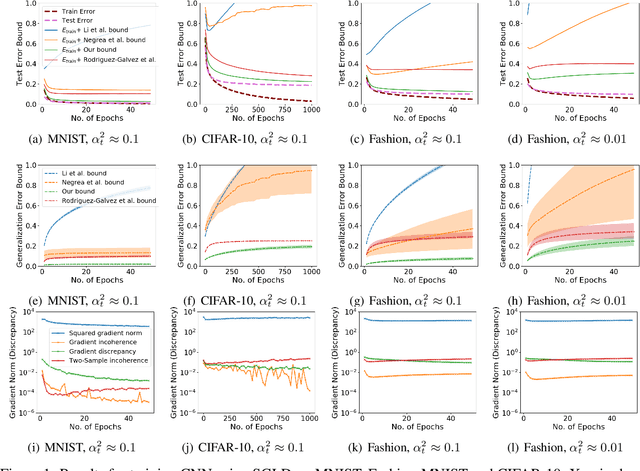
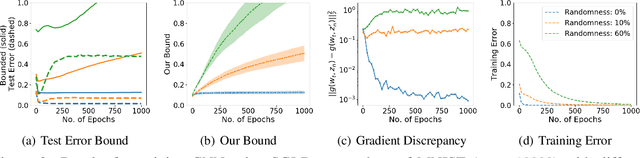
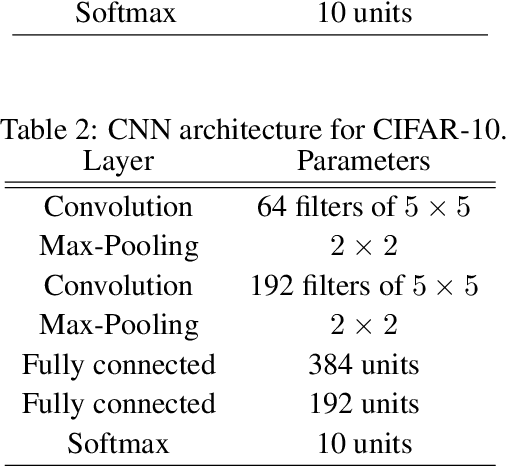
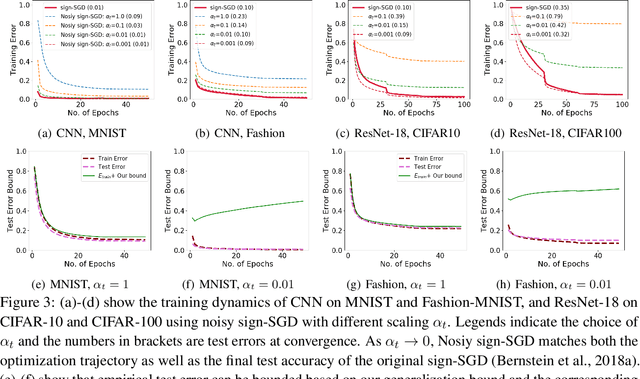
We study generalization bounds for noisy stochastic mini-batch iterative algorithms based on the notion of stability. Recent years have seen key advances in data-dependent generalization bounds for noisy iterative learning algorithms such as stochastic gradient Langevin dynamics (SGLD) based on stability (Mou et al., 2018; Li et al., 2020) and information theoretic approaches (Xu and Raginsky, 2017; Negrea et al., 2019; Steinke and Zakynthinou, 2020; Haghifam et al., 2020). In this paper, we unify and substantially generalize stability based generalization bounds and make three technical advances. First, we bound the generalization error of general noisy stochastic iterative algorithms (not necessarily gradient descent) in terms of expected (not uniform) stability. The expected stability can in turn be bounded by a Le Cam Style Divergence. Such bounds have a O(1/n) sample dependence unlike many existing bounds with O(1/\sqrt{n}) dependence. Second, we introduce Exponential Family Langevin Dynamics(EFLD) which is a substantial generalization of SGLD and which allows exponential family noise to be used with stochastic gradient descent (SGD). We establish data-dependent expected stability based generalization bounds for general EFLD algorithms. Third, we consider an important special case of EFLD: noisy sign-SGD, which extends sign-SGD using Bernoulli noise over {-1,+1}. Generalization bounds for noisy sign-SGD are implied by that of EFLD and we also establish optimization guarantees for the algorithm. Further, we present empirical results on benchmark datasets to illustrate that our bounds are non-vacuous and quantitatively much sharper than existing bounds.

Early Stopping for Deep Image Prior

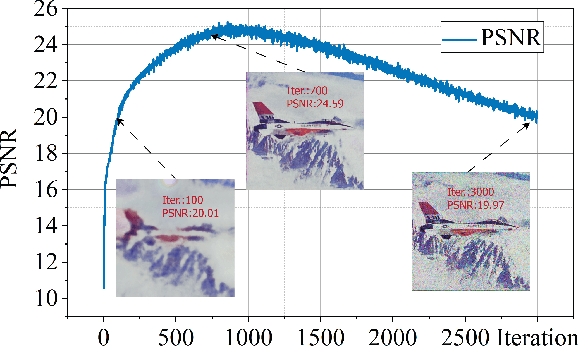
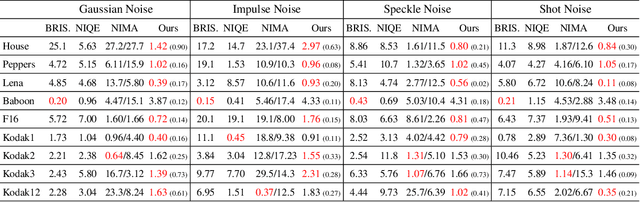
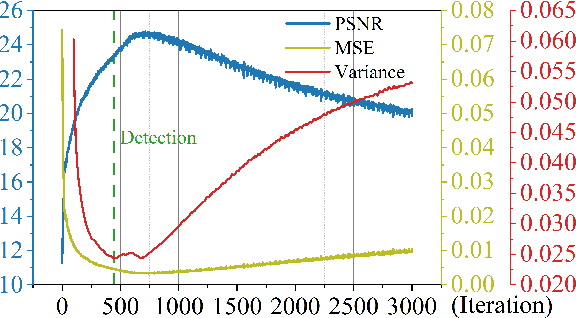
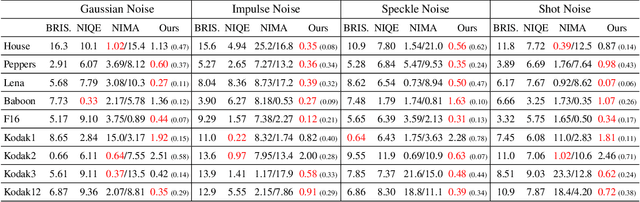
Deep image prior (DIP) and its variants have showed remarkable potential for solving inverse problems in computer vision, without any extra training data. Practical DIP models are often substantially overparameterized. During the fitting process, these models learn mostly the desired visual content first, and then pick up the potential modeling and observational noise, i.e., overfitting. Thus, the practicality of DIP often depends critically on good early stopping (ES) that captures the transition period. In this regard, the majority of DIP works for vision tasks only demonstrates the potential of the models -- reporting the peak performance against the ground truth, but provides no clue about how to operationally obtain near-peak performance without access to the groundtruth. In this paper, we set to break this practicality barrier of DIP, and propose an efficient ES strategy, which consistently detects near-peak performance across several vision tasks and DIP variants. Based on a simple measure of dispersion of consecutive DIP reconstructions, our ES method not only outpaces the existing ones -- which only work in very narrow domains, but also remains effective when combined with a number of methods that try to mitigate the overfitting. The code is available at https://github.com/sun-umn/Early_Stopping_for_DIP.

De-randomized PAC-Bayes Margin Bounds: Applications to Non-convex and Non-smooth Predictors

In spite of several notable efforts, explaining the generalization of deterministic deep nets, e.g., ReLU-nets, has remained challenging. Existing approaches usually need to bound the Lipschitz constant of such deep nets but such bounds have been shown to increase substantially with the number of training samples yielding vacuous generalization bounds [Nagarajan and Kolter, 2019a]. In this paper, we present new de-randomized PAC-Bayes margin bounds for deterministic non-convex and non-smooth predictors, e.g., ReLU-nets. The bounds depend on a trade-off between the $L_2$-norm of the weights and the effective curvature (`flatness') of the predictor, avoids any dependency on the Lipschitz constant, and yield meaningful (decreasing) bounds with increase in training set size. Our analysis first develops a de-randomization argument for non-convex but smooth predictors, e.g., linear deep networks (LDNs). We then consider non-smooth predictors which for any given input realize as a smooth predictor, e.g., ReLU-nets become some LDN for a given input, but the realized smooth predictor can be different for different inputs. For such non-smooth predictors, we introduce a new PAC-Bayes analysis that maintains distributions over the structure as well as parameters of smooth predictors, e.g., LDNs corresponding to ReLU-nets, which after de-randomization yields a bound for the deterministic non-smooth predictor. We present empirical results to illustrate the efficacy of our bounds over changing training set size and randomness in labels.

Hessian based analysis of SGD for Deep Nets: Dynamics and Generalization

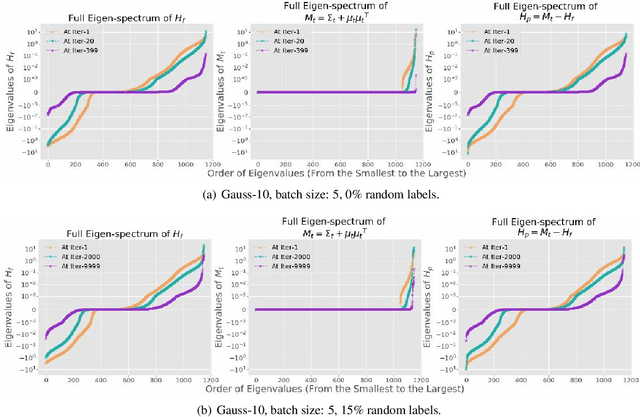
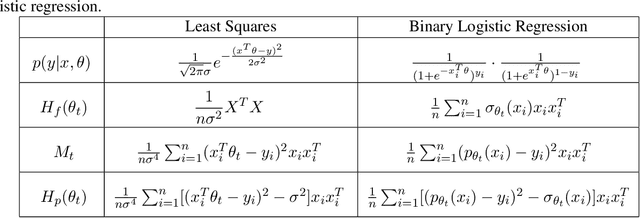
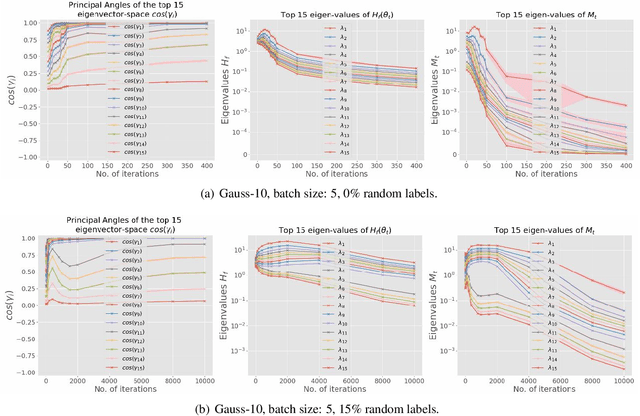
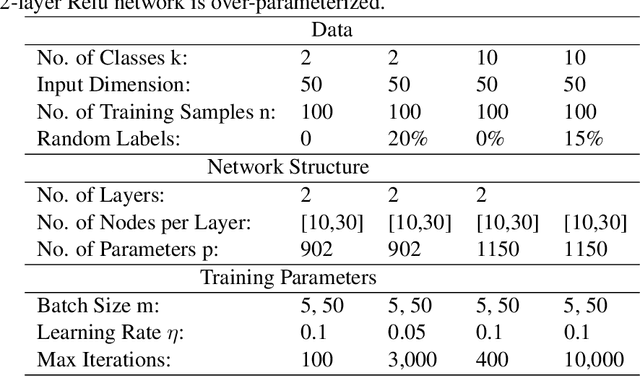
While stochastic gradient descent (SGD) and variants have been surprisingly successful for training deep nets, several aspects of the optimization dynamics and generalization are still not well understood. In this paper, we present new empirical observations and theoretical results on both the optimization dynamics and generalization behavior of SGD for deep nets based on the Hessian of the training loss and associated quantities. We consider three specific research questions: (1) what is the relationship between the Hessian of the loss and the second moment of stochastic gradients (SGs)? (2) how can we characterize the stochastic optimization dynamics of SGD with fixed and adaptive step sizes and diagonal pre-conditioning based on the first and second moments of SGs? and (3) how can we characterize a scale-invariant generalization bound of deep nets based on the Hessian of the loss, which by itself is not scale invariant? We shed light on these three questions using theoretical results supported by extensive empirical observations, with experiments on synthetic data, MNIST, and CIFAR-10, with different batch sizes, and with different difficulty levels by synthetically adding random labels.

Distributed Training with Heterogeneous Data: Bridging Median- and Mean-Based Algorithms

Recently, there is a growing interest in the study of median-based algorithms for distributed non-convex optimization. Two prominent such algorithms include signSGD with majority vote, an effective approach for communication reduction via 1-bit compression on the local gradients, and medianSGD, an algorithm recently proposed to ensure robustness against Byzantine workers. The convergence analyses for these algorithms critically rely on the assumption that all the distributed data are drawn iid from the same distribution. However, in applications such as Federated Learning, the data across different nodes or machines can be inherently heterogeneous, which violates such an iid assumption. This work analyzes signSGD and medianSGD in distributed settings with heterogeneous data. We show that these algorithms are non-convergent whenever there is some disparity between the expected median and mean over the local gradients. To overcome this gap, we provide a novel gradient correction mechanism that perturbs the local gradients with noise, together with a series results that provable close the gap between mean and median of the gradients. The proposed methods largely preserve nice properties of these methods, such as the low per-iteration communication complexity of signSGD, and further enjoy global convergence to stationary solutions. Our perturbation technique can be of independent interest when one wishes to estimate mean through a median estimator.