Bo Jiu
Radar Anti-jamming Strategy Learning via Domain-knowledge Enhanced Online Convex Optimization
Feb 29, 2024Abstract:The dynamic competition between radar and jammer systems presents a significant challenge for modern Electronic Warfare (EW), as current active learning approaches still lack sample efficiency and fail to exploit jammer's characteristics. In this paper, the competition between a frequency agile radar and a Digital Radio Frequency Memory (DRFM)-based intelligent jammer is considered. We introduce an Online Convex Optimization (OCO) framework designed to illustrate this adversarial interaction. Notably, traditional OCO algorithms exhibit suboptimal sample efficiency due to the limited information obtained per round. To address the limitations, two refined algorithms are proposed, utilizing unbiased gradient estimators that leverage the unique attributes of the jammer system. Sub-linear theoretical results on both static regret and universal regret are provided, marking a significant improvement in OCO performance. Furthermore, simulation results reveal that the proposed algorithms outperform common OCO baselines, suggesting the potential for effective deployment in real-world scenarios.
Counterfactual Regret Minimization for Anti-jamming Game of Frequency Agile Radar
Feb 21, 2022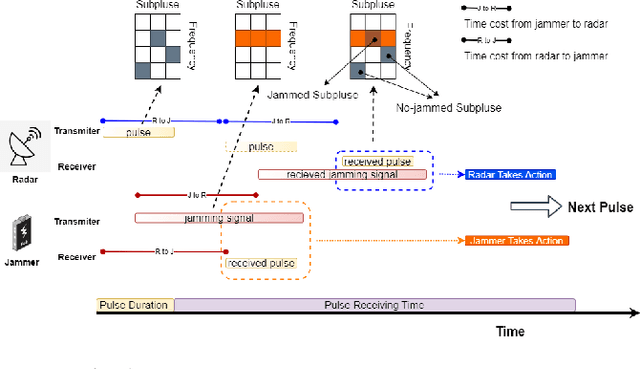
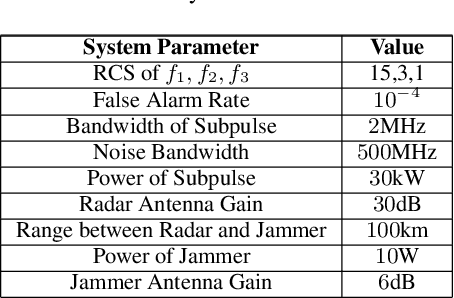
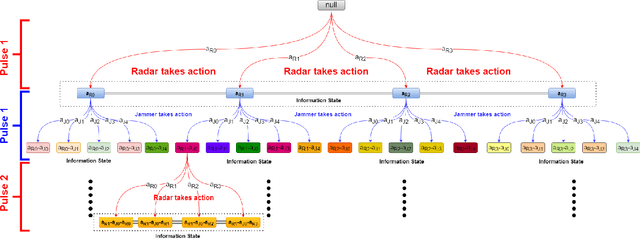
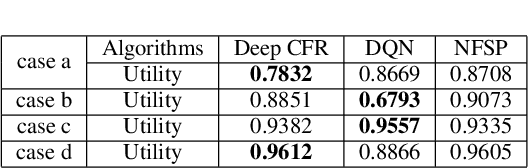
Abstract:The competition between radar and jammer is one emerging issue in modern electronic warfare, which in principle can be viewed as a non-cooperative game with two players. In this work, the competition between a frequency agile (FA) radar and a noise-modulated jammer is considered. As modern FA radar adopts coherent processing with several pulses, the competition is hence in a multiple-round way where each pulse can be modeled as one round interaction between the radar and jammer. To capture such multiple-round property as well as imperfect information inside the game, i.e., radar and jammer are unable to know the upcoming signal, we propose an extensive-form game formulation for such competition. Since the number of game information states grows exponentially with respect to number of pulses, finding Nash Equilibrium (NE) strategies may be a computationally intractable task. To effectively solve the game, a learning-based algorithm called deep Counterfactual Regret Minimization (CFR) is utilized. Numerical simulations demonstrates the effectiveness of deep CFR algorithm for approximately finding NE and obtaining the best response strategy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge