Efficient Estimation of Sensor Biases for the 3-Dimensional Asynchronous Multi-Sensor System

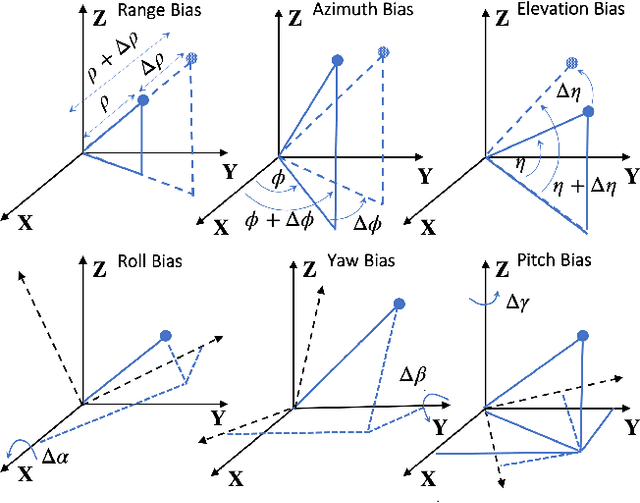
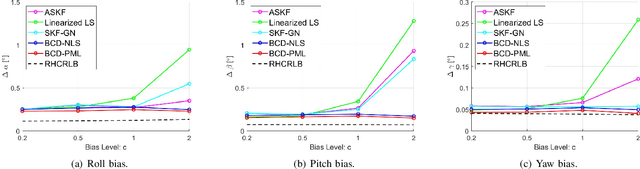
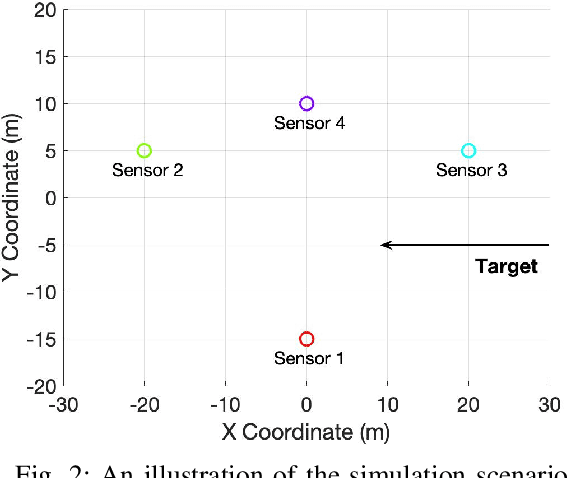
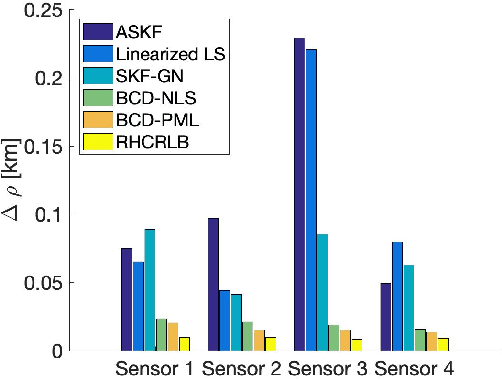
An important preliminary procedure in multi-sensor data fusion is sensor registration, and the key step in this procedure is to estimate sensor biases from their noisy measurements. There are generally two difficulties in this bias estimation problem: one is the unknown target states which serve as the nuisance variables in the estimation problem, and the other is the highly nonlinear coordinate transformation between the local and global coordinate systems of the sensors. In this paper, we focus on the 3-dimensional asynchronous multi-sensor scenario and propose a weighted nonlinear least squares (NLS) formulation by assuming that there is a target moving with a nearly constant velocity. We propose two possible choices of the weighting matrix in the NLS formulation, which correspond to classical NLS estimation and maximum likelihood (ML) estimation, respectively. To address the intrinsic nonlinearity, we propose a block coordinate descent (BCD) algorithm for solving the formulated problem, which alternately updates different kinds of bias estimates. Specifically, the proposed BCD algorithm involves solving linear LS problems and nonconvex quadratically constrained quadratic program (QCQP) problems with special structures. Instead of adopting the semidefinite relaxation technique, we develop a much more computationally efficient algorithm (with global performance guarantee under certain conditions) to solve the nonconvex QCQP subproblems. The effectiveness and efficiency of the proposed BCD algorithm are demonstrated via numerical simulations.