Gaussian Processes with Linear Multiple Kernel: Spectrum Design and Distributed Learning for Multi-Dimensional Data

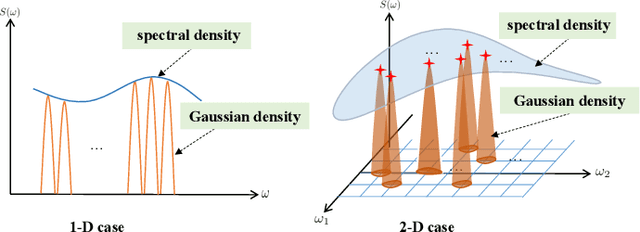
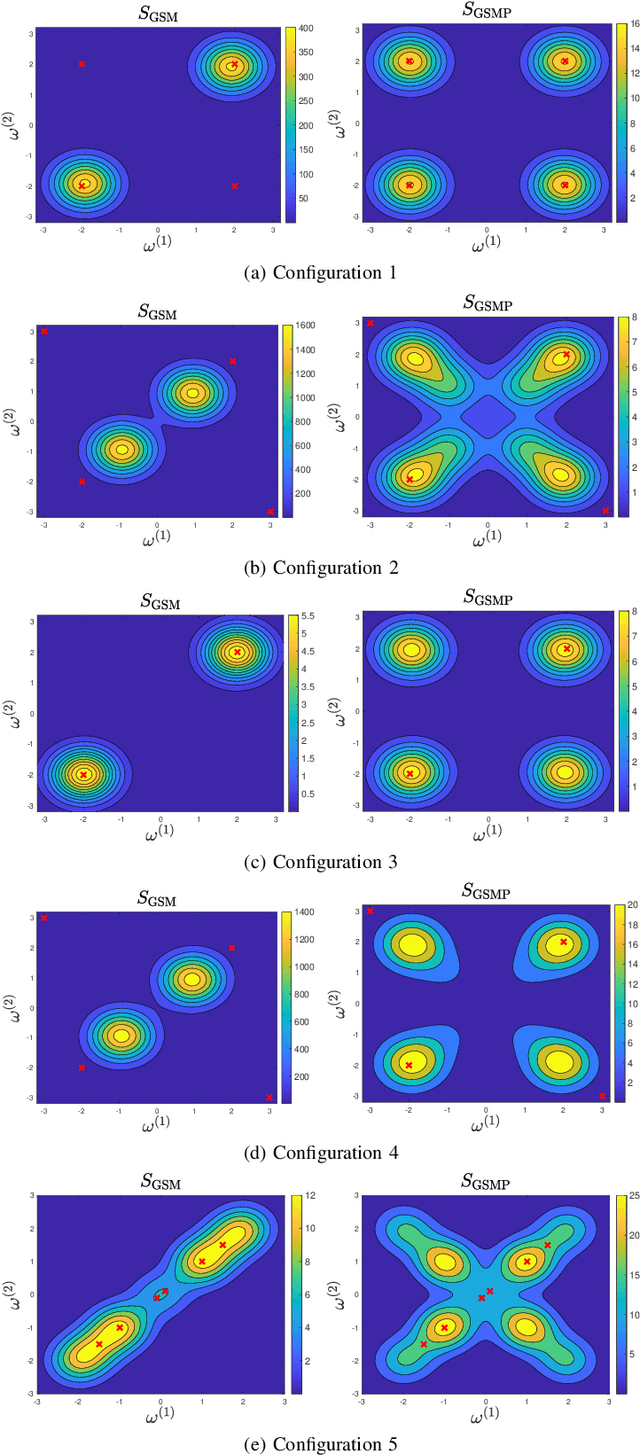
Gaussian processes (GPs) have emerged as a prominent technique for machine learning and signal processing. A key component in GP modeling is the choice of kernel, and linear multiple kernels (LMKs) have become an attractive kernel class due to their powerful modeling capacity and interpretability. This paper focuses on the grid spectral mixture (GSM) kernel, an LMK that can approximate arbitrary stationary kernels. Specifically, we propose a novel GSM kernel formulation for multi-dimensional data that reduces the number of hyper-parameters compared to existing formulations, while also retaining a favorable optimization structure and approximation capability. In addition, to make the large-scale hyper-parameter optimization in the GSM kernel tractable, we first introduce the distributed SCA (DSCA) algorithm. Building on this, we propose the doubly distributed SCA (D$^2$SCA) algorithm based on the alternating direction method of multipliers (ADMM) framework, which allows us to cooperatively learn the GSM kernel in the context of big data while maintaining data privacy. Furthermore, we tackle the inherent communication bandwidth restriction in distributed frameworks, by quantizing the hyper-parameters in D$^2$SCA, resulting in the quantized doubly distributed SCA (QD$^2$SCA) algorithm. Theoretical analysis establishes convergence guarantees for the proposed algorithms, while experiments on diverse datasets demonstrate the superior prediction performance and efficiency of our methods.