Scalable Random Feature Latent Variable Models
Paper and Code
Oct 23, 2024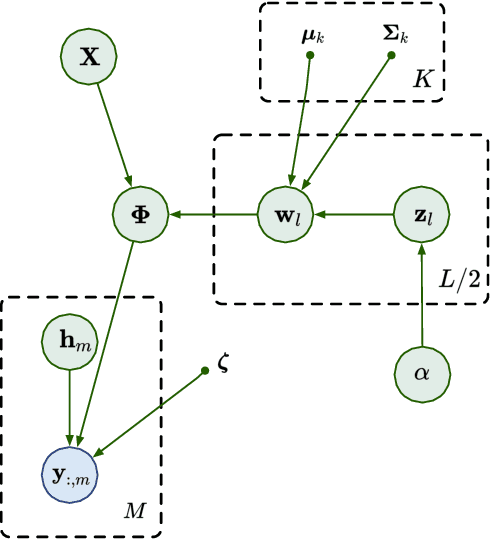



Random feature latent variable models (RFLVMs) represent the state-of-the-art in latent variable models, capable of handling non-Gaussian likelihoods and effectively uncovering patterns in high-dimensional data. However, their heavy reliance on Monte Carlo sampling results in scalability issues which makes it difficult to use these models for datasets with a massive number of observations. To scale up RFLVMs, we turn to the optimization-based variational Bayesian inference (VBI) algorithm which is known for its scalability compared to sampling-based methods. However, implementing VBI for RFLVMs poses challenges, such as the lack of explicit probability distribution functions (PDFs) for the Dirichlet process (DP) in the kernel learning component, and the incompatibility of existing VBI algorithms with RFLVMs. To address these issues, we introduce a stick-breaking construction for DP to obtain an explicit PDF and a novel VBI algorithm called ``block coordinate descent variational inference" (BCD-VI). This enables the development of a scalable version of RFLVMs, or in short, SRFLVM. Our proposed method shows scalability, computational efficiency, superior performance in generating informative latent representations and the ability of imputing missing data across various real-world datasets, outperforming state-of-the-art competitors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge