Wrong but Useful: Trajectory Value Beyond Answer Correctness in Multi-Agent Messages

Multi-agent reasoning systems often use agreement, confidence, or automated scores to decide which messages should shape a final answer. Such filtering assumes that a message likely to be correct is also worth keeping. Yet a wrong answer can contain a useful decomposition, constraint, or scientific principle. We test this distinction with Diverse Hypothesis Deliberation (DHD), a controlled measurement protocol that caches five independently generated messages and replays the same downstream solver, called the integrator, with each message available or hidden. The replay comparison measures a message's trajectory value: whether making the message available helps or harms subsequent reasoning. Across five mathematics and science benchmarks and two openly available model families, gpt-oss-120b and gemma-4-31B-it, wrong-helpful messages appear in every benchmark-model combination. Among wrong-answer messages that change final correctness, more than four in ten changes are helpful in each model. Controlled repeats show that the number of repeatable message effects is unlikely to arise from replay variation alone (p=0.0002). A focused intervention on repeatable wrong-helpful messages finds that the complete message works best, while retaining its reasoning preserves more success than retaining only its answer; the source of the complete-message advantage remains open. Within the same problem, repeated trajectory-value evidence also identifies a better keep-or-remove choice than answer correctness alone. Answer correctness is therefore informative but does not determine trajectory value. DHD measures this missing property and produces reusable labels for learning when agents should listen.

Nested Sampling: A Critical and Comprehensive Theoretical Guide

The nested sampling (NS) technique has gained widespread attention, particularly in cosmology and astronomy, due to its ability to efficiently explore high-likelihood regions - a feature akin to an implicit likelihood optimization that underlies its success. While the full theoretical derivation of NS is complex and involves several approximations, the central challenge lies in sampling from the likelihood-constrained priors, which is crucial for its performance. This work provides a comprehensive and detailed exposition of NS derivation, clarifying both its theoretical foundations and practical challenges. We provide a thorough description of the NS procedure, emphasizing both its strengths and potential limitations. In doing so, this work seeks to deepen understanding of the method and to foster the development of future enhancements, novel variants, and more efficient implementations across a wide range of scientific applications. Thus, the main contribution of this work is twofold: it serves both as a tutorial for newcomers to the field and as a critical review for experienced practitioners.

Bayesian Ensembling: Insights from Online Optimization and Empirical Bayes

We revisit the classical problem of Bayesian ensembles and address the challenge of learning optimal combinations of Bayesian models in an online, continual learning setting. To this end, we reinterpret existing approaches such as Bayesian model averaging (BMA) and Bayesian stacking through a novel empirical Bayes lens, shedding new light on the limitations and pathologies of BMA. Further motivated by insights from online optimization, we propose Online Bayesian Stacking (OBS), a method that optimizes the log-score over predictive distributions to adaptively combine Bayesian models. A key contribution of our work is establishing a novel connection between OBS and portfolio selection, bridging Bayesian ensemble learning with a rich, well-studied theoretical framework that offers efficient algorithms and extensive regret analysis. We further clarify the relationship between OBS and online BMA, showing that they optimize related but distinct cost functions. Through theoretical analysis and empirical evaluation, we identify scenarios where OBS outperforms online BMA and provide principled guidance on when practitioners should prefer one approach over the other.

Enhancing Graphical Lasso: A Robust Scheme for Non-Stationary Mean Data

This work addresses the problem of graph learning from data following a Gaussian Graphical Model (GGM) with a time-varying mean. Graphical Lasso (GL), the standard method for estimating sparse precision matrices, assumes that the observed data follows a zero-mean Gaussian distribution. However, this assumption is often violated in real-world scenarios where the mean evolves over time due to external influences, trends, or regime shifts. When the mean is not properly accounted for, applying GL directly can lead to estimating a biased precision matrix, hence hindering the graph learning task. To overcome this limitation, we propose Graphical Lasso with Adaptive Targeted Adaptive Importance Sampling (GL-ATAIS), an iterative method that jointly estimates the time-varying mean and the precision matrix. Our approach integrates Bayesian inference with frequentist estimation, leveraging importance sampling to obtain an estimate of the mean while using a regularized maximum likelihood estimator to infer the precision matrix. By iteratively refining both estimates, GL-ATAIS mitigates the bias introduced by time-varying means, leading to more accurate graph recovery. Our numerical evaluation demonstrates the impact of properly accounting for time-dependent means and highlights the advantages of GL-ATAIS over standard GL in recovering the true graph structure.

Optimality in importance sampling: a gentle survey

The performance of the Monte Carlo sampling methods relies on the crucial choice of a proposal density. The notion of optimality is fundamental to design suitable adaptive procedures of the proposal density within Monte Carlo schemes. This work is an exhaustive review around the concept of optimality in importance sampling. Several frameworks are described and analyzed, such as the marginal likelihood approximation for model selection, the use of multiple proposal densities, a sequence of tempered posteriors, and noisy scenarios including the applications to approximate Bayesian computation (ABC) and reinforcement learning, to name a few. Some theoretical and empirical comparisons are also provided.

Decentralized Online Ensembles of Gaussian Processes for Multi-Agent Systems

Flexible and scalable decentralized learning solutions are fundamentally important in the application of multi-agent systems. While several recent approaches introduce (ensembles of) kernel machines in the distributed setting, Bayesian solutions are much more limited. We introduce a fully decentralized, asymptotically exact solution to computing the random feature approximation of Gaussian processes. We further address the choice of hyperparameters by introducing an ensembling scheme for Bayesian multiple kernel learning based on online Bayesian model averaging. The resulting algorithm is tested against Bayesian and frequentist methods on simulated and real-world datasets.

Fusion of Gaussian Processes Predictions with Monte Carlo Sampling

In science and engineering, we often work with models designed for accurate prediction of variables of interest. Recognizing that these models are approximations of reality, it becomes desirable to apply multiple models to the same data and integrate their outcomes. In this paper, we operate within the Bayesian paradigm, relying on Gaussian processes as our models. These models generate predictive probability density functions (pdfs), and the objective is to integrate them systematically, employing both linear and log-linear pooling. We introduce novel approaches for log-linear pooling, determining input-dependent weights for the predictive pdfs of the Gaussian processes. The aggregation of the pdfs is realized through Monte Carlo sampling, drawing samples of weights from their posterior. The performance of these methods, as well as those based on linear pooling, is demonstrated using a synthetic dataset.

CAMEO: Curiosity Augmented Metropolis for Exploratory Optimal Policies

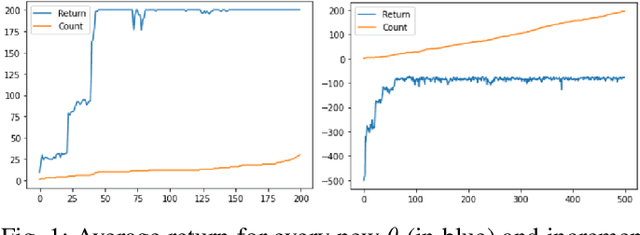
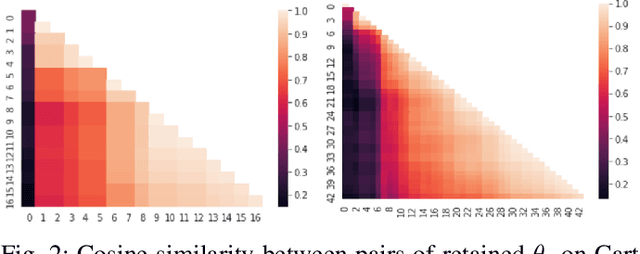
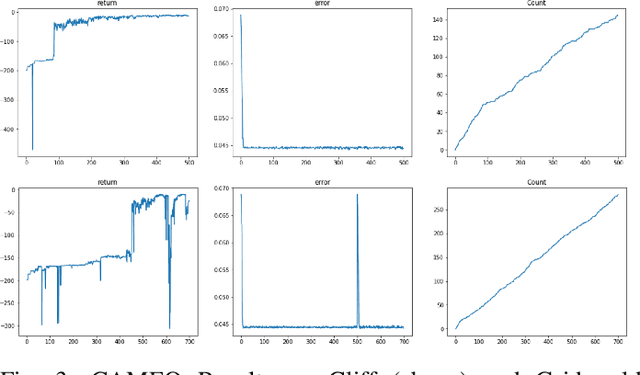
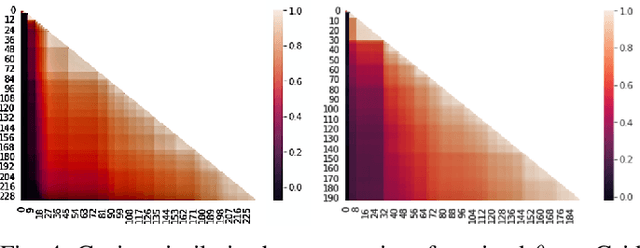
Reinforcement Learning has drawn huge interest as a tool for solving optimal control problems. Solving a given problem (task or environment) involves converging towards an optimal policy. However, there might exist multiple optimal policies that can dramatically differ in their behaviour; for example, some may be faster than the others but at the expense of greater risk. We consider and study a distribution of optimal policies. We design a curiosity-augmented Metropolis algorithm (CAMEO), such that we can sample optimal policies, and such that these policies effectively adopt diverse behaviours, since this implies greater coverage of the different possible optimal policies. In experimental simulations we show that CAMEO indeed obtains policies that all solve classic control problems, and even in the challenging case of environments that provide sparse rewards. We further show that the different policies we sample present different risk profiles, corresponding to interesting practical applications in interpretability, and represents a first step towards learning the distribution of optimal policies itself.

Optimality in Noisy Importance Sampling

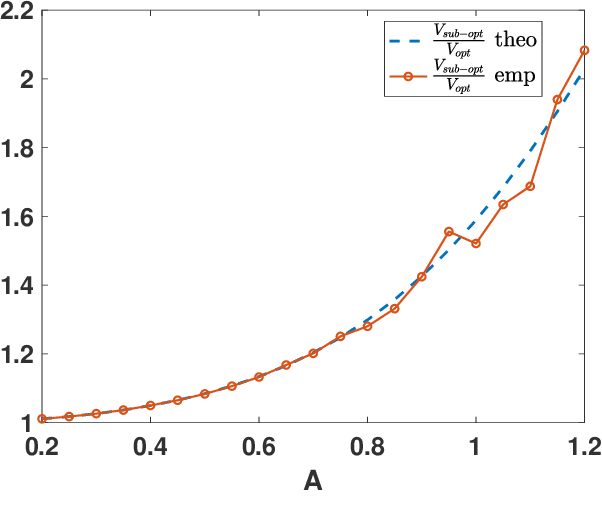
In this work, we analyze the noisy importance sampling (IS), i.e., IS working with noisy evaluations of the target density. We present the general framework and derive optimal proposal densities for noisy IS estimators. The optimal proposals incorporate the information of the variance of the noisy realizations, proposing points in regions where the noise power is higher. We also compare the use of the optimal proposals with previous optimality approaches considered in a noisy IS framework.

Marginal likelihood computation for model selection and hypothesis testing: an extensive review

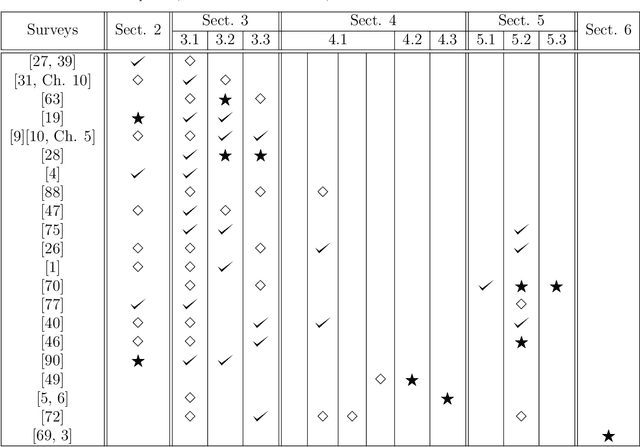
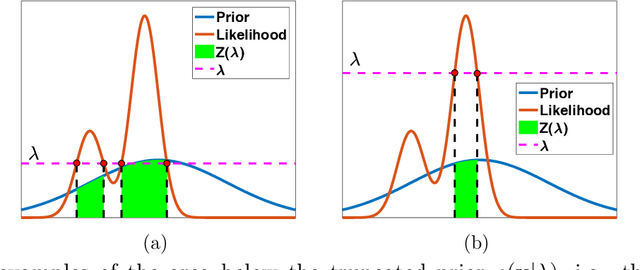
This is an up-to-date introduction to, and overview of, marginal likelihood computation for model selection and hypothesis testing. Computing normalizing constants of probability models (or ratio of constants) is a fundamental issue in many applications in statistics, applied mathematics, signal processing and machine learning. This article provides a comprehensive study of the state-of-the-art of the topic. We highlight limitations, benefits, connections and differences among the different techniques. Problems and possible solutions with the use of improper priors are also described. Some of the most relevant methodologies are compared through theoretical comparisons and numerical experiments.