Optimality in importance sampling: a gentle survey
Paper and Code
Feb 11, 2025
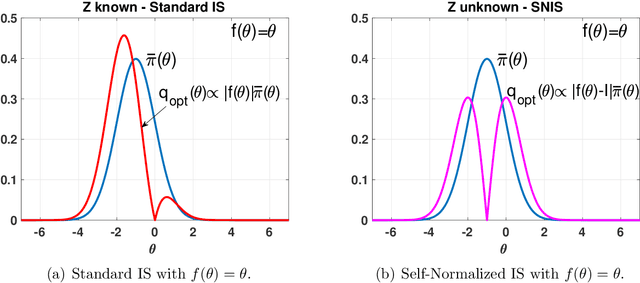

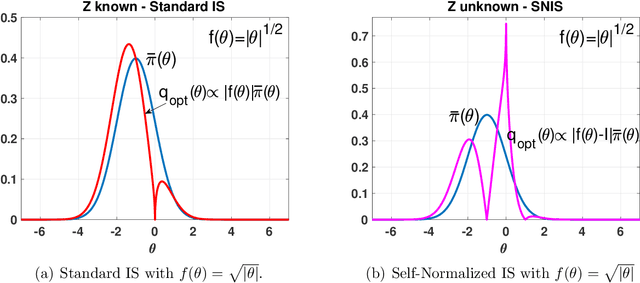
The performance of the Monte Carlo sampling methods relies on the crucial choice of a proposal density. The notion of optimality is fundamental to design suitable adaptive procedures of the proposal density within Monte Carlo schemes. This work is an exhaustive review around the concept of optimality in importance sampling. Several frameworks are described and analyzed, such as the marginal likelihood approximation for model selection, the use of multiple proposal densities, a sequence of tempered posteriors, and noisy scenarios including the applications to approximate Bayesian computation (ABC) and reinforcement learning, to name a few. Some theoretical and empirical comparisons are also provided.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge