On Counterfactual Interventions in Vector Autoregressive Models

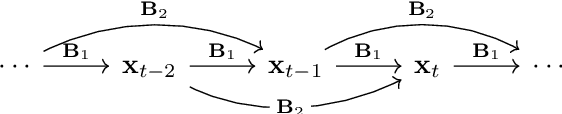
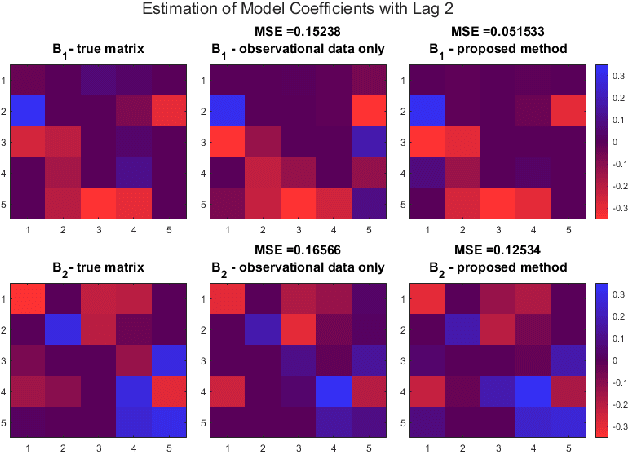
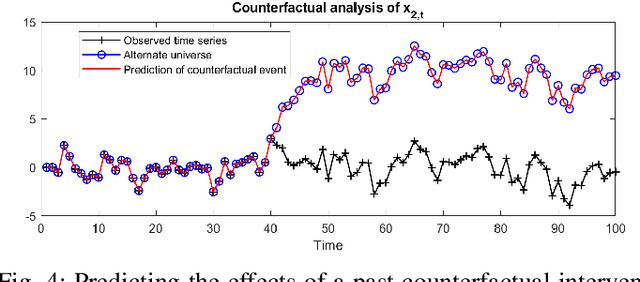
Counterfactual reasoning allows us to explore hypothetical scenarios in order to explain the impacts of our decisions. However, addressing such inquires is impossible without establishing the appropriate mathematical framework. In this work, we introduce the problem of counterfactual reasoning in the context of vector autoregressive (VAR) processes. We also formulate the inference of a causal model as a joint regression task where for inference we use both data with and without interventions. After learning the model, we exploit linearity of the VAR model to make exact predictions about the effects of counterfactual interventions. Furthermore, we quantify the total causal effects of past counterfactual interventions. The source code for this project is freely available at https://github.com/KurtButler/counterfactual_interventions.

Explainable Learning with Gaussian Processes

The field of explainable artificial intelligence (XAI) attempts to develop methods that provide insight into how complicated machine learning methods make predictions. Many methods of explanation have focused on the concept of feature attribution, a decomposition of the model's prediction into individual contributions corresponding to each input feature. In this work, we explore the problem of feature attribution in the context of Gaussian process regression (GPR). We take a principled approach to defining attributions under model uncertainty, extending the existing literature. We show that although GPR is a highly flexible and non-parametric approach, we can derive interpretable, closed-form expressions for the feature attributions. When using integrated gradients as an attribution method, we show that the attributions of a GPR model also follow a Gaussian process distribution, which quantifies the uncertainty in attribution arising from uncertainty in the model. We demonstrate, both through theory and experimentation, the versatility and robustness of this approach. We also show that, when applicable, the exact expressions for GPR attributions are both more accurate and less computationally expensive than the approximations currently used in practice. The source code for this project is freely available under MIT license at https://github.com/KurtButler/2024_attributions_paper.

Fusion of Gaussian Processes Predictions with Monte Carlo Sampling

In science and engineering, we often work with models designed for accurate prediction of variables of interest. Recognizing that these models are approximations of reality, it becomes desirable to apply multiple models to the same data and integrate their outcomes. In this paper, we operate within the Bayesian paradigm, relying on Gaussian processes as our models. These models generate predictive probability density functions (pdfs), and the objective is to integrate them systematically, employing both linear and log-linear pooling. We introduce novel approaches for log-linear pooling, determining input-dependent weights for the predictive pdfs of the Gaussian processes. The aggregation of the pdfs is realized through Monte Carlo sampling, drawing samples of weights from their posterior. The performance of these methods, as well as those based on linear pooling, is demonstrated using a synthetic dataset.

Dagma-DCE: Interpretable, Non-Parametric Differentiable Causal Discovery

We introduce Dagma-DCE, an interpretable and model-agnostic scheme for differentiable causal discovery. Current non- or over-parametric methods in differentiable causal discovery use opaque proxies of ``independence'' to justify the inclusion or exclusion of a causal relationship. We show theoretically and empirically that these proxies may be arbitrarily different than the actual causal strength. Juxtaposed to existing differentiable causal discovery algorithms, \textsc{Dagma-DCE} uses an interpretable measure of causal strength to define weighted adjacency matrices. In a number of simulated datasets, we show our method achieves state-of-the-art level performance. We additionally show that \textsc{Dagma-DCE} allows for principled thresholding and sparsity penalties by domain-experts. The code for our method is available open-source at https://github.com/DanWaxman/DAGMA-DCE, and can easily be adapted to arbitrary differentiable models.

Reinforcement Learning for UAV Autonomous Navigation, Mapping and Target Detection

In this paper, we study a joint detection, mapping and navigation problem for a single unmanned aerial vehicle (UAV) equipped with a low complexity radar and flying in an unknown environment. The goal is to optimize its trajectory with the purpose of maximizing the mapping accuracy and, at the same time, to avoid areas where measurements might not be sufficiently informative from the perspective of a target detection. This problem is formulated as a Markov decision process (MDP) where the UAV is an agent that runs either a state estimator for target detection and for environment mapping, and a reinforcement learning (RL) algorithm to infer its own policy of navigation (i.e., the control law). Numerical results show the feasibility of the proposed idea, highlighting the UAV's capability of autonomously exploring areas with high probability of target detection while reconstructing the surrounding environment.

Dynamic Radar Network of UAVs: A Joint Navigation and Tracking Approach

Nowadays there is a growing research interest on the possibility of enriching small flying robots with autonomous sensing and online navigation capabilities. This will enable a large number of applications spanning from remote surveillance to logistics, smarter cities and emergency aid in hazardous environments. In this context, an emerging problem is to track unauthorized small unmanned aerial vehicles (UAVs) hiding behind buildings or concealing in large UAV networks. In contrast with current solutions mainly based on static and on-ground radars, this paper proposes the idea of a dynamic radar network of UAVs for real-time and high-accuracy tracking of malicious targets. To this end, we describe a solution for real-time navigation of UAVs to track a dynamic target using heterogeneously sensed information. Such information is shared by the UAVs with their neighbors via multi-hops, allowing tracking the target by a local Bayesian estimator running at each agent. Since not all the paths are equal in terms of information gathering point-of-view, the UAVs plan their own trajectory by minimizing the posterior covariance matrix of the target state under UAV kinematic and anti-collision constraints. Our results show how a dynamic network of radars attains better localization results compared to a fixed configuration and how the on-board sensor technology impacts the accuracy in tracking a target with different radar cross sections, especially in non line-of-sight (NLOS) situations.