Enhancing Graphical Lasso: A Robust Scheme for Non-Stationary Mean Data
Paper and Code
Mar 25, 2025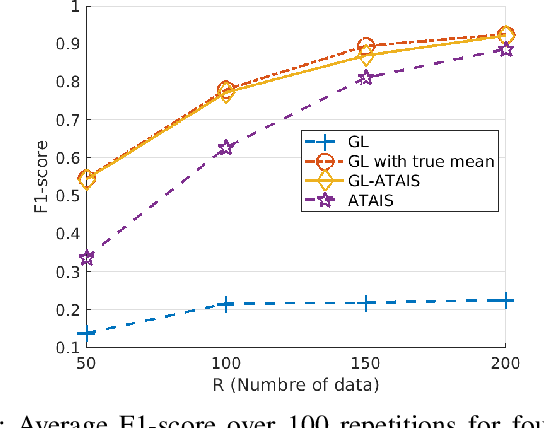
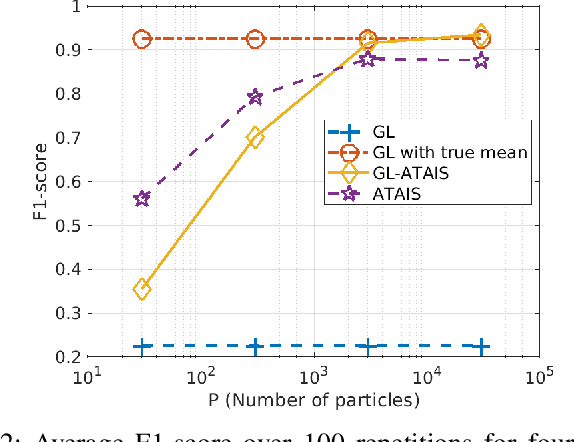
This work addresses the problem of graph learning from data following a Gaussian Graphical Model (GGM) with a time-varying mean. Graphical Lasso (GL), the standard method for estimating sparse precision matrices, assumes that the observed data follows a zero-mean Gaussian distribution. However, this assumption is often violated in real-world scenarios where the mean evolves over time due to external influences, trends, or regime shifts. When the mean is not properly accounted for, applying GL directly can lead to estimating a biased precision matrix, hence hindering the graph learning task. To overcome this limitation, we propose Graphical Lasso with Adaptive Targeted Adaptive Importance Sampling (GL-ATAIS), an iterative method that jointly estimates the time-varying mean and the precision matrix. Our approach integrates Bayesian inference with frequentist estimation, leveraging importance sampling to obtain an estimate of the mean while using a regularized maximum likelihood estimator to infer the precision matrix. By iteratively refining both estimates, GL-ATAIS mitigates the bias introduced by time-varying means, leading to more accurate graph recovery. Our numerical evaluation demonstrates the impact of properly accounting for time-dependent means and highlights the advantages of GL-ATAIS over standard GL in recovering the true graph structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge