Diffusion Self-Weighted Guidance for Offline Reinforcement Learning

Offline reinforcement learning (RL) recovers the optimal policy $\pi$ given historical observations of an agent. In practice, $\pi$ is modeled as a weighted version of the agent's behavior policy $\mu$, using a weight function $w$ working as a critic of the agent's behavior. Though recent approaches to offline RL based on diffusion models have exhibited promising results, the computation of the required scores is challenging due to their dependence on the unknown $w$. In this work, we alleviate this issue by constructing a diffusion over both the actions and the weights. With the proposed setting, the required scores are directly obtained from the diffusion model without learning extra networks. Our main conceptual contribution is a novel guidance method, where guidance (which is a function of $w$) comes from the same diffusion model, therefore, our proposal is termed Self-Weighted Guidance (SWG). We show that SWG generates samples from the desired distribution on toy examples and performs on par with state-of-the-art methods on D4RL's challenging environments, while maintaining a streamlined training pipeline. We further validate SWG through ablation studies on weight formulations and scalability.

Towards SFW sampling for diffusion models via external conditioning

Score-based generative models (SBM), also known as diffusion models, are the de facto state of the art for image synthesis. Despite their unparalleled performance, SBMs have recently been in the spotlight for being tricked into creating not-safe-for-work (NSFW) content, such as violent images and non-consensual nudity. Current approaches that prevent unsafe generation are based on the models' own knowledge, and the majority of them require fine-tuning. This article explores the use of external sources for ensuring safe outputs in SBMs. Our safe-for-work (SFW) sampler implements a Conditional Trajectory Correction step that guides the samples away from undesired regions in the ambient space using multimodal models as the source of conditioning. Furthermore, using Contrastive Language Image Pre-training (CLIP), our method admits user-defined NSFW classes, which can vary in different settings. Our experiments on the text-to-image SBM Stable Diffusion validate that the proposed SFW sampler effectively reduces the generation of explicit content while being competitive with other fine-tuning-based approaches, as assessed via independent NSFW detectors. Moreover, we evaluate the impact of the SFW sampler on image quality and show that the proposed correction scheme comes at a minor cost with negligible effect on samples not needing correction. Our study confirms the suitability of the SFW sampler towards aligned SBM models and the potential of using model-agnostic conditioning for the prevention of unwanted images.

Avoiding mode collapse in diffusion models fine-tuned with reinforcement learning

Fine-tuning foundation models via reinforcement learning (RL) has proven promising for aligning to downstream objectives. In the case of diffusion models (DMs), though RL training improves alignment from early timesteps, critical issues such as training instability and mode collapse arise. We address these drawbacks by exploiting the hierarchical nature of DMs: we train them dynamically at each epoch with a tailored RL method, allowing for continual evaluation and step-by-step refinement of the model performance (or alignment). Furthermore, we find that not every denoising step needs to be fine-tuned to align DMs to downstream tasks. Consequently, in addition to clipping, we regularise model parameters at distinct learning phases via a sliding-window approach. Our approach, termed Hierarchical Reward Fine-tuning (HRF), is validated on the Denoising Diffusion Policy Optimisation method, where we show that models trained with HRF achieve better preservation of diversity in downstream tasks, thus enhancing the fine-tuning robustness and at uncompromising mean rewards.

Detection of manatee vocalisations using the Audio Spectrogram Transformer

The Antillean manatee (\emph{Trichechus manatus}) is an endangered herbivorous aquatic mammal whose role as an ecological balancer and umbrella species underscores the importance of its conservation. An innovative approach to monitor manatee populations is passive acoustic monitoring (PAM), where vocalisations are extracted from submarine audio. We propose a novel end-to-end approach to detect manatee vocalisations building on the Audio Spectrogram Transformer (AST). In a transfer learning spirit, we fine-tune AST to detect manatee calls by redesigning its filterbanks and adapting a real-world dataset containing partial positive labels. Our experimental evaluation reveals the two key features of the proposed model: i) it performs on par with the state of the art without requiring hand-tuned denoising or detection stages, and ii) it can successfully identify missed vocalisations in the training dataset, thus reducing the workload of expert bioacoustic labellers. This work is a preliminary relevant step to develop novel, user-friendly tools for the conservation of the different species of manatees.

Asynchronous Graph Generators

We introduce the asynchronous graph generator (AGG), a novel graph neural network architecture for multi-channel time series which models observations as nodes on a dynamic graph and can thus perform data imputation by transductive node generation. Completely free from recurrent components or assumptions about temporal regularity, AGG represents measurements, timestamps and metadata directly in the nodes via learnable embeddings, to then leverage attention to learn expressive relationships across the variables of interest. This way, the proposed architecture implicitly learns a causal graph representation of sensor measurements which can be conditioned on unseen timestamps and metadata to predict new measurements by an expansion of the learnt graph. The proposed AGG is compared both conceptually and empirically to previous work, and the impact of data augmentation on the performance of AGG is also briefly discussed. Our experiments reveal that AGG achieved state-of-the-art results in time series data imputation, classification and prediction for the benchmark datasets Beijing Air Quality, PhysioNet Challenge 2012 and UCI localisation.

Greedy online change point detection

Standard online change point detection (CPD) methods tend to have large false discovery rates as their detections are sensitive to outliers. To overcome this drawback, we propose Greedy Online Change Point Detection (GOCPD), a computationally appealing method which finds change points by maximizing the probability of the data coming from the (temporal) concatenation of two independent models. We show that, for time series with a single change point, this objective is unimodal and thus CPD can be accelerated via ternary search with logarithmic complexity. We demonstrate the effectiveness of GOCPD on synthetic data and validate our findings on real-world univariate and multivariate settings.

Gaussian process deconvolution

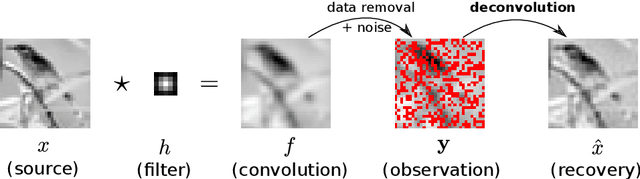
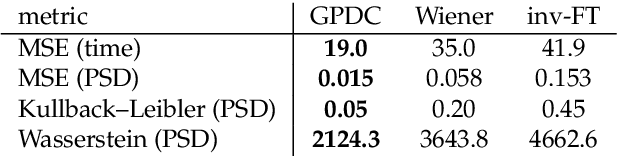
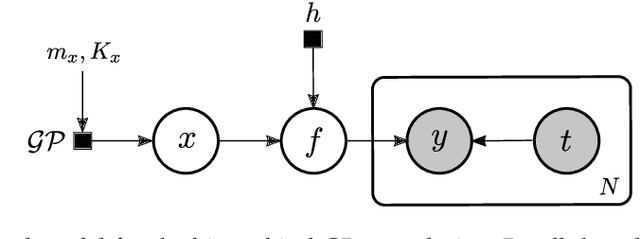
Let us consider the deconvolution problem, that is, to recover a latent source $x(\cdot)$ from the observations $\mathbf{y} = [y_1,\ldots,y_N]$ of a convolution process $y = x\star h + \eta$, where $\eta$ is an additive noise, the observations in $\mathbf{y}$ might have missing parts with respect to $y$, and the filter $h$ could be unknown. We propose a novel strategy to address this task when $x$ is a continuous-time signal: we adopt a Gaussian process (GP) prior on the source $x$, which allows for closed-form Bayesian nonparametric deconvolution. We first analyse the direct model to establish the conditions under which the model is well defined. Then, we turn to the inverse problem, where we study i) some necessary conditions under which Bayesian deconvolution is feasible, and ii) to which extent the filter $h$ can be learnt from data or approximated for the blind deconvolution case. The proposed approach, termed Gaussian process deconvolution (GPDC) is compared to other deconvolution methods conceptually, via illustrative examples, and using real-world datasets.

Computationally-efficient initialisation of GPs: The generalised variogram method

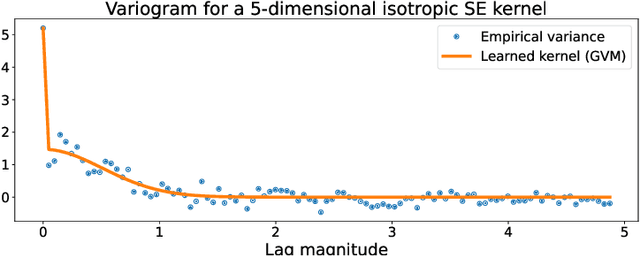
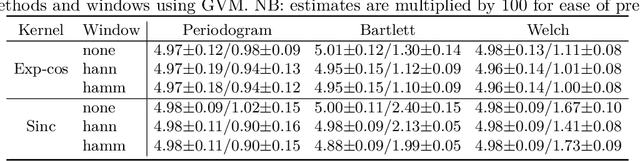
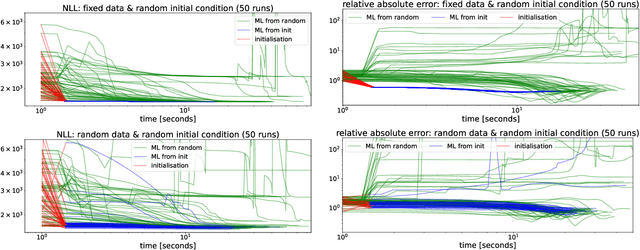
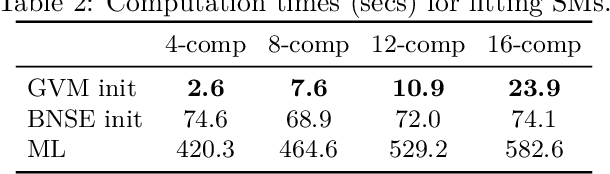
We present a computationally-efficient strategy to find the hyperparameters of a Gaussian process (GP) avoiding the computation of the likelihood function. The found hyperparameters can then be used directly for regression or passed as initial conditions to maximum-likelihood (ML) training. Motivated by the fact that training a GP via ML is equivalent (on average) to minimising the KL-divergence between the true and learnt model, we set to explore different metrics/divergences among GPs that are computationally inexpensive and provide estimates close to those of ML. In particular, we identify the GP hyperparameters by matching the empirical covariance to a parametric candidate, proposing and studying various measures of discrepancy. Our proposal extends the Variogram method developed by the geostatistics literature and thus is referred to as the Generalised Variogram method (GVM). In addition to the theoretical presentation of GVM, we provide experimental validation in terms of accuracy, consistency with ML and computational complexity for different kernels using synthetic and real-world data.

Nonstationary multi-output Gaussian processes via harmonizable spectral mixtures

Kernel design for Multi-output Gaussian Processes (MOGP) has received increased attention recently. In particular, the Multi-Output Spectral Mixture kernel (MOSM) arXiv:1709.01298 approach has been praised as a general model in the sense that it extends other approaches such as Linear Model of Corregionalization, Intrinsic Corregionalization Model and Cross-Spectral Mixture. MOSM relies on Cram\'er's theorem to parametrise the power spectral densities (PSD) as a Gaussian mixture, thus, having a structural restriction: by assuming the existence of a PSD, the method is only suited for multi-output stationary applications. We develop a nonstationary extension of MOSM by proposing the family of harmonizable kernels for MOGPs, a class of kernels that contains both stationary and a vast majority of non-stationary processes. A main contribution of the proposed harmonizable kernels is that they automatically identify a possible nonstationary behaviour meaning that practitioners do not need to choose between stationary or non-stationary kernels. The proposed method is first validated on synthetic data with the purpose of illustrating the key properties of our approach, and then compared to existing MOGP methods on two real-world settings from finance and electroencephalography.

Studying the Interplay between Information Loss and Operation Loss in Representations for Classification

Information-theoretic measures have been widely adopted in the design of features for learning and decision problems. Inspired by this, we look at the relationship between i) a weak form of information loss in the Shannon sense and ii) the operation loss in the minimum probability of error (MPE) sense when considering a family of lossy continuous representations (features) of a continuous observation. We present several results that shed light on this interplay. Our first result offers a lower bound on a weak form of information loss as a function of its respective operation loss when adopting a discrete lossy representation (quantization) instead of the original raw observation. From this, our main result shows that a specific form of vanishing information loss (a weak notion of asymptotic informational sufficiency) implies a vanishing MPE loss (or asymptotic operational sufficiency) when considering a general family of lossy continuous representations. Our theoretical findings support the observation that the selection of feature representations that attempt to capture informational sufficiency is appropriate for learning, but this selection is a rather conservative design principle if the intended goal is achieving MPE in classification. Supporting this last point, and under some structural conditions, we show that it is possible to adopt an alternative notion of informational sufficiency (strictly weaker than pure sufficiency in the mutual information sense) to achieve operational sufficiency in learning.