Understanding Encoder-Decoder Structures in Machine Learning Using Information Measures

We present new results to model and understand the role of encoder-decoder design in machine learning (ML) from an information-theoretic angle. We use two main information concepts, information sufficiency (IS) and mutual information loss (MIL), to represent predictive structures in machine learning. Our first main result provides a functional expression that characterizes the class of probabilistic models consistent with an IS encoder-decoder latent predictive structure. This result formally justifies the encoder-decoder forward stages many modern ML architectures adopt to learn latent (compressed) representations for classification. To illustrate IS as a realistic and relevant model assumption, we revisit some known ML concepts and present some interesting new examples: invariant, robust, sparse, and digital models. Furthermore, our IS characterization allows us to tackle the fundamental question of how much performance (predictive expressiveness) could be lost, using the cross entropy risk, when a given encoder-decoder architecture is adopted in a learning setting. Here, our second main result shows that a mutual information loss quantifies the lack of expressiveness attributed to the choice of a (biased) encoder-decoder ML design. Finally, we address the problem of universal cross-entropy learning with an encoder-decoder design where necessary and sufficiency conditions are established to meet this requirement. In all these results, Shannon's information measures offer new interpretations and explanations for representation learning.

Fault Detection and Monitoring using an Information-Driven Strategy: Method, Theory, and Application

The ability to detect when a system undergoes an incipient fault is of paramount importance in preventing a critical failure. In this work, we propose an information-driven fault detection method based on a novel concept drift detector. The method is tailored to identifying drifts in input-output relationships of additive noise models (i.e., model drifts) and is based on a distribution-free mutual information (MI) estimator. Our scheme does not require prior faulty examples and can be applied distribution-free over a large class of system models. Our core contributions are twofold. First, we demonstrate the connection between fault detection, model drift detection, and testing independence between two random variables. Second, we prove several theoretical properties of the proposed MI-based fault detection scheme: (i) strong consistency, (ii) exponentially fast detection of the non-faulty case, and (iii) control of both significance levels and power of the test. To conclude, we validate our theory with synthetic data and the benchmark dataset N-CMAPSS of aircraft turbofan engines. These empirical results support the usefulness of our methodology in many practical and realistic settings, and the theoretical results show performance guarantees that other methods cannot offer.

Gaussian process deconvolution

Let us consider the deconvolution problem, that is, to recover a latent source $x(\cdot)$ from the observations $\mathbf{y} = [y_1,\ldots,y_N]$ of a convolution process $y = x\star h + \eta$, where $\eta$ is an additive noise, the observations in $\mathbf{y}$ might have missing parts with respect to $y$, and the filter $h$ could be unknown. We propose a novel strategy to address this task when $x$ is a continuous-time signal: we adopt a Gaussian process (GP) prior on the source $x$, which allows for closed-form Bayesian nonparametric deconvolution. We first analyse the direct model to establish the conditions under which the model is well defined. Then, we turn to the inverse problem, where we study i) some necessary conditions under which Bayesian deconvolution is feasible, and ii) to which extent the filter $h$ can be learnt from data or approximated for the blind deconvolution case. The proposed approach, termed Gaussian process deconvolution (GPDC) is compared to other deconvolution methods conceptually, via illustrative examples, and using real-world datasets.

Lossy Compression for Robust Unsupervised Time-Series Anomaly Detection

A new Lossy Causal Temporal Convolutional Neural Network Autoencoder for anomaly detection is proposed in this work. Our framework uses a rate-distortion loss and an entropy bottleneck to learn a compressed latent representation for the task. The main idea of using a rate-distortion loss is to introduce representation flexibility that ignores or becomes robust to unlikely events with distinctive patterns, such as anomalies. These anomalies manifest as unique distortion features that can be accurately detected in testing conditions. This new architecture allows us to train a fully unsupervised model that has high accuracy in detecting anomalies from a distortion score despite being trained with some portion of unlabelled anomalous data. This setting is in stark contrast to many of the state-of-the-art unsupervised methodologies that require the model to be only trained on "normal data". We argue that this partially violates the concept of unsupervised training for anomaly detection as the model uses an informed decision that selects what is normal from abnormal for training. Additionally, there is evidence to suggest it also effects the models ability at generalisation. We demonstrate that models that succeed in the paradigm where they are only trained on normal data fail to be robust when anomalous data is injected into the training. In contrast, our compression-based approach converges to a robust representation that tolerates some anomalous distortion. The robust representation achieved by a model using a rate-distortion loss can be used in a more realistic unsupervised anomaly detection scheme.

Studying the Interplay between Information Loss and Operation Loss in Representations for Classification

Information-theoretic measures have been widely adopted in the design of features for learning and decision problems. Inspired by this, we look at the relationship between i) a weak form of information loss in the Shannon sense and ii) the operation loss in the minimum probability of error (MPE) sense when considering a family of lossy continuous representations (features) of a continuous observation. We present several results that shed light on this interplay. Our first result offers a lower bound on a weak form of information loss as a function of its respective operation loss when adopting a discrete lossy representation (quantization) instead of the original raw observation. From this, our main result shows that a specific form of vanishing information loss (a weak notion of asymptotic informational sufficiency) implies a vanishing MPE loss (or asymptotic operational sufficiency) when considering a general family of lossy continuous representations. Our theoretical findings support the observation that the selection of feature representations that attempt to capture informational sufficiency is appropriate for learning, but this selection is a rather conservative design principle if the intended goal is achieving MPE in classification. Supporting this last point, and under some structural conditions, we show that it is possible to adopt an alternative notion of informational sufficiency (strictly weaker than pure sufficiency in the mutual information sense) to achieve operational sufficiency in learning.

Data-Driven Representations for Testing Independence: Modeling, Analysis and Connection with Mutual Information Estimation

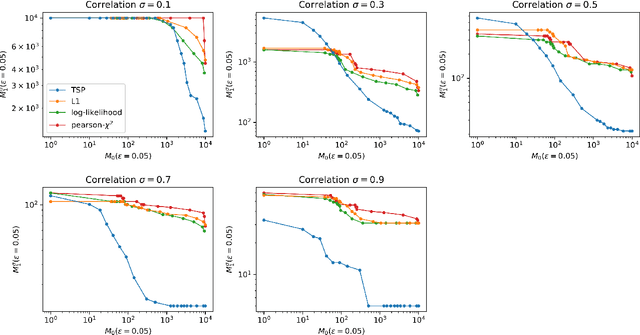
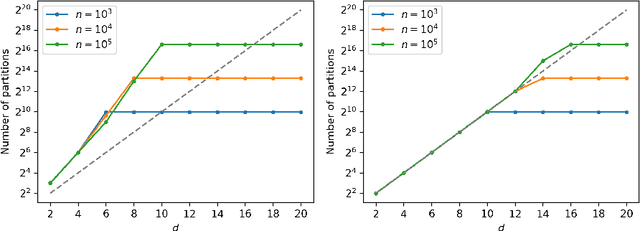
This work addresses testing the independence of two continuous and finite-dimensional random variables from the design of a data-driven partition. The empirical log-likelihood statistic is adopted to approximate the sufficient statistics of an oracle test against independence (that knows the two hypotheses). It is shown that approximating the sufficient statistics of the oracle test offers a learning criterion for designing a data-driven partition that connects with the problem of mutual information estimation. Applying these ideas in the context of a data-dependent tree-structured partition (TSP), we derive conditions on the TSP's parameters to achieve a strongly consistent distribution-free test of independence over the family of probabilities equipped with a density. Complementing this result, we present finite-length results that show our TSP scheme's capacity to detect the scenario of independence structurally with the data-driven partition as well as new sampling complexity bounds for this detection. Finally, some experimental analyses provide evidence regarding our scheme's advantage for testing independence compared with some strategies that do not use data-driven representations.

Shannon Entropy Estimation in $\infty$-Alphabets from Convergence Results

The problem of Shannon entropy estimation in countable infinite alphabets is addressed from the study and use of convergence results of the entropy functional, which is known to be discontinuous with respect to the total variation distance in $\infty$-alphabets. Sufficient conditions for the convergence of the entropy are used, including scenarios with both finitely and infinitely supported assumptions on the distributions. From this new perspective, four plug-in histogram-based estimators are studied showing that convergence results are instrumental to derive new strong consistency and rate of convergences results. Different scenarios and conditions are used on both the estimators and the underlying distribution, considering for example finite and unknown supported assumptions and summable tail bounded conditions.