Fault Detection and Monitoring using an Information-Driven Strategy: Method, Theory, and Application

The ability to detect when a system undergoes an incipient fault is of paramount importance in preventing a critical failure. In this work, we propose an information-driven fault detection method based on a novel concept drift detector. The method is tailored to identifying drifts in input-output relationships of additive noise models (i.e., model drifts) and is based on a distribution-free mutual information (MI) estimator. Our scheme does not require prior faulty examples and can be applied distribution-free over a large class of system models. Our core contributions are twofold. First, we demonstrate the connection between fault detection, model drift detection, and testing independence between two random variables. Second, we prove several theoretical properties of the proposed MI-based fault detection scheme: (i) strong consistency, (ii) exponentially fast detection of the non-faulty case, and (iii) control of both significance levels and power of the test. To conclude, we validate our theory with synthetic data and the benchmark dataset N-CMAPSS of aircraft turbofan engines. These empirical results support the usefulness of our methodology in many practical and realistic settings, and the theoretical results show performance guarantees that other methods cannot offer.

Data-Driven Representations for Testing Independence: Modeling, Analysis and Connection with Mutual Information Estimation

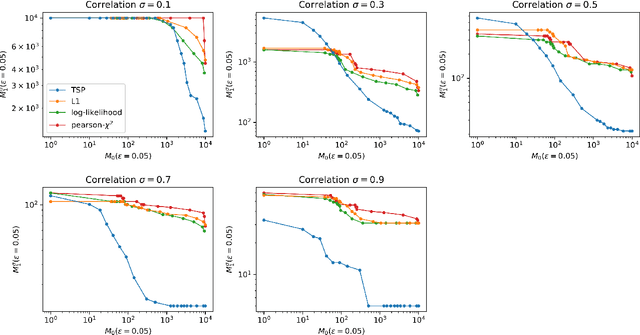
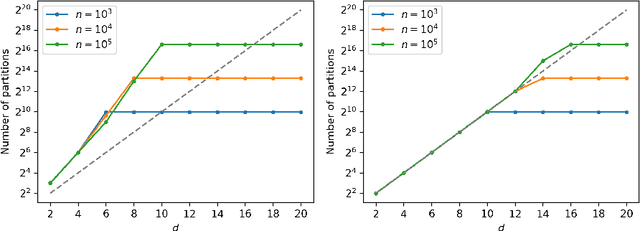
This work addresses testing the independence of two continuous and finite-dimensional random variables from the design of a data-driven partition. The empirical log-likelihood statistic is adopted to approximate the sufficient statistics of an oracle test against independence (that knows the two hypotheses). It is shown that approximating the sufficient statistics of the oracle test offers a learning criterion for designing a data-driven partition that connects with the problem of mutual information estimation. Applying these ideas in the context of a data-dependent tree-structured partition (TSP), we derive conditions on the TSP's parameters to achieve a strongly consistent distribution-free test of independence over the family of probabilities equipped with a density. Complementing this result, we present finite-length results that show our TSP scheme's capacity to detect the scenario of independence structurally with the data-driven partition as well as new sampling complexity bounds for this detection. Finally, some experimental analyses provide evidence regarding our scheme's advantage for testing independence compared with some strategies that do not use data-driven representations.