Learning to Optimise Wind Farms with Graph Transformers

This work proposes a novel data-driven model capable of providing accurate predictions for the power generation of all wind turbines in wind farms of arbitrary layout, yaw angle configurations and wind conditions. The proposed model functions by encoding a wind farm into a fully-connected graph and processing the graph representation through a graph transformer. The graph transformer surrogate is shown to generalise well and is able to uncover latent structural patterns within the graph representation of wind farms. It is demonstrated how the resulting surrogate model can be used to optimise yaw angle configurations using genetic algorithms, achieving similar levels of accuracy to industrially-standard wind farm simulation tools while only taking a fraction of the computational cost.

Gaussian process deconvolution

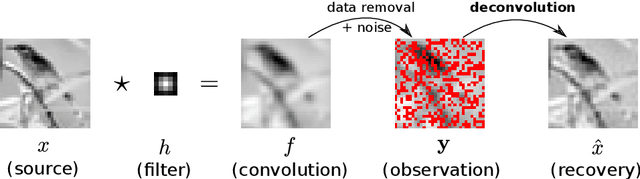
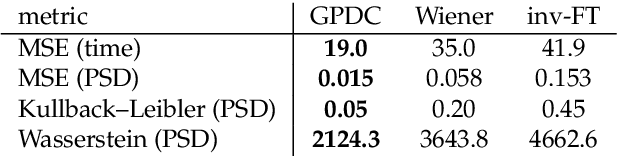
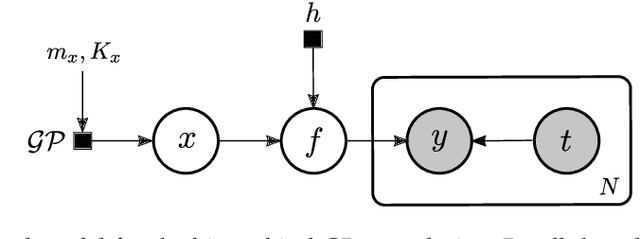
Let us consider the deconvolution problem, that is, to recover a latent source $x(\cdot)$ from the observations $\mathbf{y} = [y_1,\ldots,y_N]$ of a convolution process $y = x\star h + \eta$, where $\eta$ is an additive noise, the observations in $\mathbf{y}$ might have missing parts with respect to $y$, and the filter $h$ could be unknown. We propose a novel strategy to address this task when $x$ is a continuous-time signal: we adopt a Gaussian process (GP) prior on the source $x$, which allows for closed-form Bayesian nonparametric deconvolution. We first analyse the direct model to establish the conditions under which the model is well defined. Then, we turn to the inverse problem, where we study i) some necessary conditions under which Bayesian deconvolution is feasible, and ii) to which extent the filter $h$ can be learnt from data or approximated for the blind deconvolution case. The proposed approach, termed Gaussian process deconvolution (GPDC) is compared to other deconvolution methods conceptually, via illustrative examples, and using real-world datasets.

The Wasserstein-Fourier Distance for Stationary Time Series

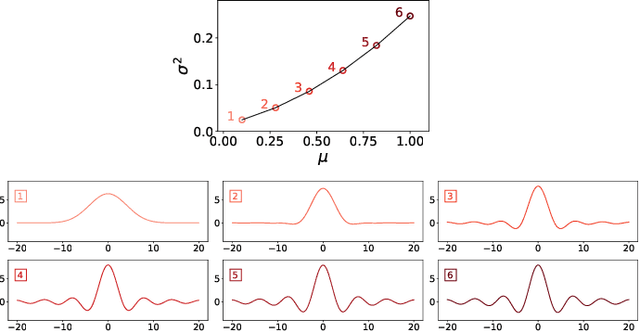
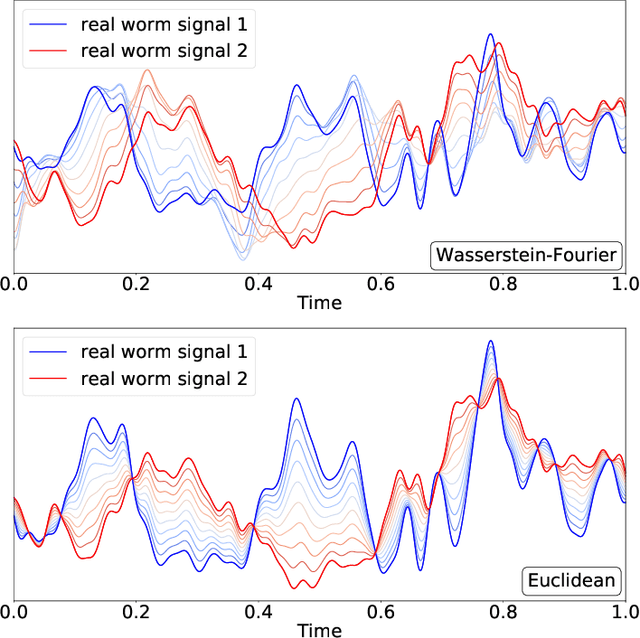
We introduce a novel framework for analysing stationary time series based on optimal transport distances and spectral embeddings. First, we represent time series by their power spectral density (PSD), which summarises the signal energy spread across the Fourier spectrum. Second, we endow the space of PSDs with the Wasserstein distance, which capitalises its unique ability to preserve the geometric information of a set of distributions. These two steps enable us to define the Wasserstein-Fourier (WF) distance, which allows us to compare stationary time series even when they differ in sampling rate, length, magnitude and phase. We analyse the features of WF by blending the properties of the Wasserstein distance and those of the Fourier transform. The proposed WF distance is then used in three sets of key time series applications considering real-world datasets: (i) interpolation of time series leading to data augmentation, (ii) dimensionality reduction via non-linear PCA, and (iii) parametric and non-parametric classification tasks. Our conceptual and experimental findings validate the general concept of using divergences of distributions, especially the Wasserstein distance, to analyse time series through comparing their spectral representations.