Detection of manatee vocalisations using the Audio Spectrogram Transformer

The Antillean manatee (\emph{Trichechus manatus}) is an endangered herbivorous aquatic mammal whose role as an ecological balancer and umbrella species underscores the importance of its conservation. An innovative approach to monitor manatee populations is passive acoustic monitoring (PAM), where vocalisations are extracted from submarine audio. We propose a novel end-to-end approach to detect manatee vocalisations building on the Audio Spectrogram Transformer (AST). In a transfer learning spirit, we fine-tune AST to detect manatee calls by redesigning its filterbanks and adapting a real-world dataset containing partial positive labels. Our experimental evaluation reveals the two key features of the proposed model: i) it performs on par with the state of the art without requiring hand-tuned denoising or detection stages, and ii) it can successfully identify missed vocalisations in the training dataset, thus reducing the workload of expert bioacoustic labellers. This work is a preliminary relevant step to develop novel, user-friendly tools for the conservation of the different species of manatees.

Computationally-efficient initialisation of GPs: The generalised variogram method

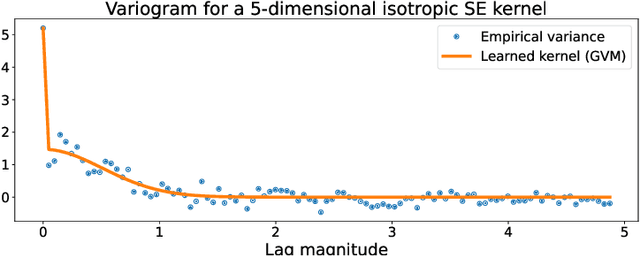
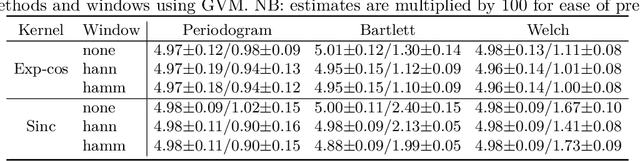
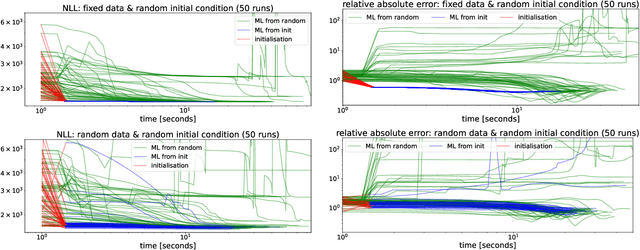
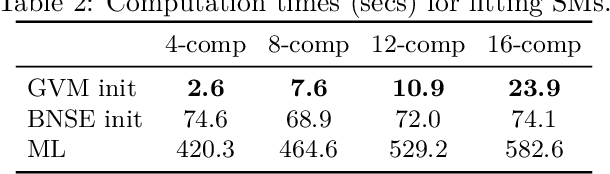
We present a computationally-efficient strategy to find the hyperparameters of a Gaussian process (GP) avoiding the computation of the likelihood function. The found hyperparameters can then be used directly for regression or passed as initial conditions to maximum-likelihood (ML) training. Motivated by the fact that training a GP via ML is equivalent (on average) to minimising the KL-divergence between the true and learnt model, we set to explore different metrics/divergences among GPs that are computationally inexpensive and provide estimates close to those of ML. In particular, we identify the GP hyperparameters by matching the empirical covariance to a parametric candidate, proposing and studying various measures of discrepancy. Our proposal extends the Variogram method developed by the geostatistics literature and thus is referred to as the Generalised Variogram method (GVM). In addition to the theoretical presentation of GVM, we provide experimental validation in terms of accuracy, consistency with ML and computational complexity for different kernels using synthetic and real-world data.

Towards Optimally Weighted Physics-Informed Neural Networks in Ocean Modelling

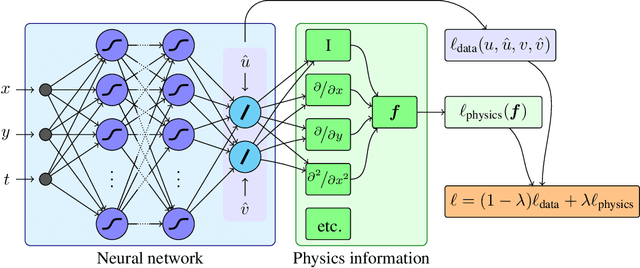
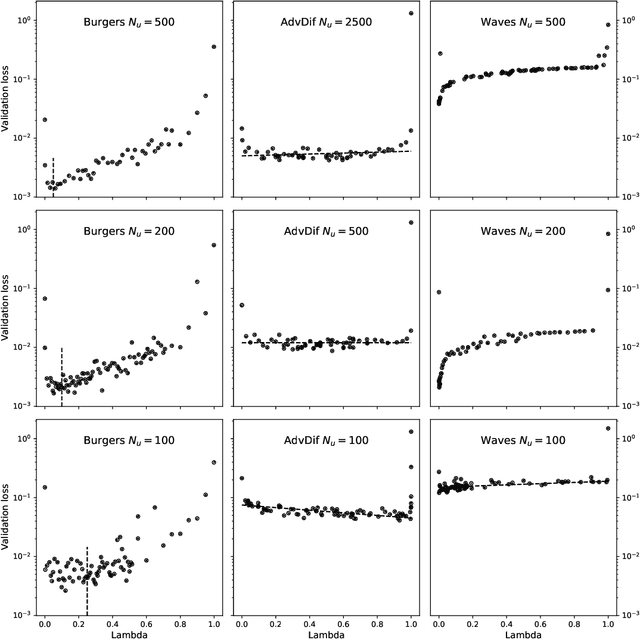
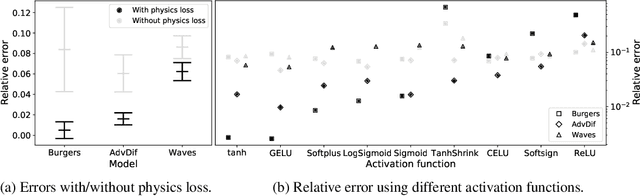
The carbon pump of the world's ocean plays a vital role in the biosphere and climate of the earth, urging improved understanding of the functions and influences of the ocean for climate change analyses. State-of-the-art techniques are required to develop models that can capture the complexity of ocean currents and temperature flows. This work explores the benefits of using physics-informed neural networks (PINNs) for solving partial differential equations related to ocean modeling; such as the Burgers, wave, and advection-diffusion equations. We explore the trade-offs of using data vs. physical models in PINNs for solving partial differential equations. PINNs account for the deviation from physical laws in order to improve learning and generalization. We observed how the relative weight between the data and physical model in the loss function influence training results, where small data sets benefit more from the added physics information.

Gaussian process imputation of multiple financial series

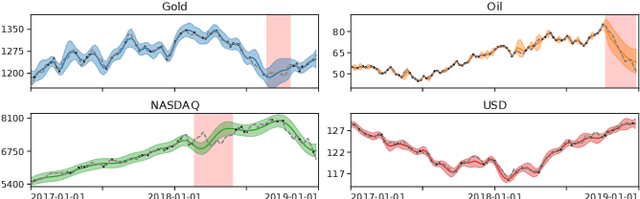
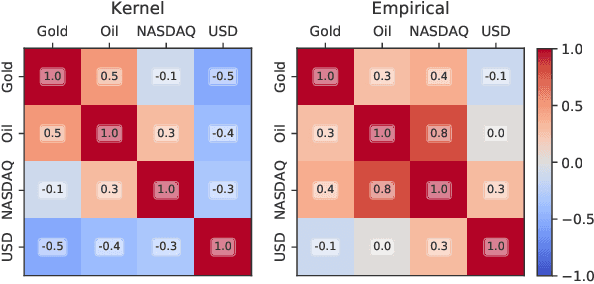
In Financial Signal Processing, multiple time series such as financial indicators, stock prices and exchange rates are strongly coupled due to their dependence on the latent state of the market and therefore they are required to be jointly analysed. We focus on learning the relationships among financial time series by modelling them through a multi-output Gaussian process (MOGP) with expressive covariance functions. Learning these market dependencies among financial series is crucial for the imputation and prediction of financial observations. The proposed model is validated experimentally on two real-world financial datasets for which their correlations across channels are analysed. We compare our model against other MOGPs and the independent Gaussian process on real financial data.

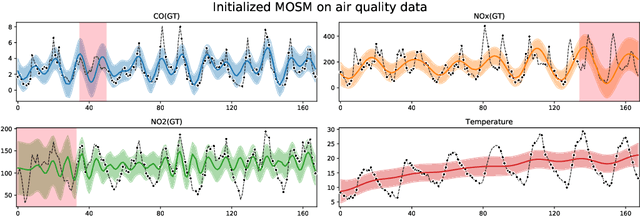
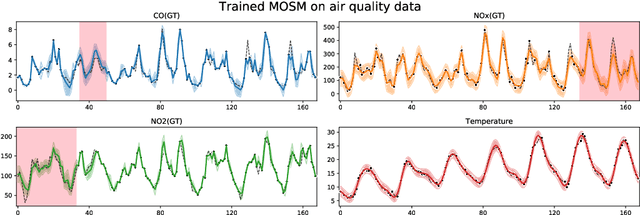
MOGPTK: The Multi-Output Gaussian Process Toolkit

We present MOGPTK, a Python package for multi-channel data modelling using Gaussian processes (GP). The aim of this toolkit is to make multi-output GP (MOGP) models accessible to researchers, data scientists, and practitioners alike. MOGPTK uses a Python front-end, relies on the GPflow suite and is built on a TensorFlow back-end, thus enabling GPU-accelerated training. The toolkit facilitates implementing the entire pipeline of GP modelling, including data loading, parameter initialization, model learning, parameter interpretation, up to data imputation and extrapolation. MOGPTK implements the main multi-output covariance kernels from literature, as well as spectral-based parameter initialization strategies. The source code, tutorials and examples in the form of Jupyter notebooks, together with the API documentation, can be found at http://github.com/GAMES-UChile/mogptk