Commercial Persuasion in AI-Mediated Conversations

As Large Language Models (LLMs) become a primary interface between users and the web, companies face growing economic incentives to embed commercial influence into AI-mediated conversations. We present two preregistered experiments (N = 2,012) in which participants selected a book to receive from a large eBook catalog using either a traditional search engine or a conversational LLM agent powered by one of five frontier models. Unbeknownst to participants, a fifth of all products were randomly designated as sponsored and promoted in different ways. We find that LLM-driven persuasion nearly triples the rate at which users select sponsored products compared to traditional search placement (61.2% vs. 22.4%), while the vast majority of participants fail to detect any promotional steering. Explicit "Sponsored" labels do not significantly reduce persuasion, and instructing the model to conceal its intent makes its influence nearly invisible (detection accuracy < 10%). Altogether, our results indicate that conversational AI can covertly redirect consumer choices at scale, and that existing transparency mechanisms may be insufficient to protect users.

Bayesian autoregressive spectral estimation

Autoregressive (AR) time series models are widely used in parametric spectral estimation (SE), where the power spectral density (PSD) of the time series is approximated by that of the \emph{best-fit} AR model, which is available in closed form. Since AR parameters are usually found via maximum-likelihood, least squares or the method of moments, AR-based SE fails to account for the uncertainty of the approximate PSD, and thus only yields point estimates. We propose to handle the uncertainty related to the AR approximation by finding the full posterior distribution of the AR parameters to then propagate this uncertainty to the PSD approximation by \emph{integrating out the AR parameters}; we implement this concept by assuming two different priors over the model noise. Through practical experiments, we show that the proposed Bayesian autoregressive spectral estimation (BASE) provides point estimates that follow closely those of standard autoregressive spectral estimation (ASE), while also providing error bars. BASE is validated against ASE and the Periodogram on both synthetic and real-world signals.

Gaussian process imputation of multiple financial series

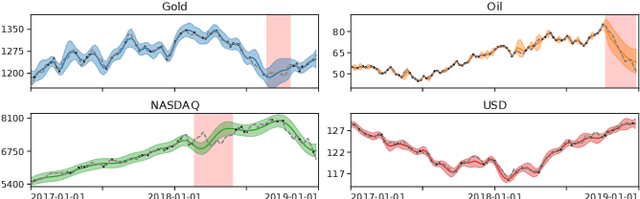
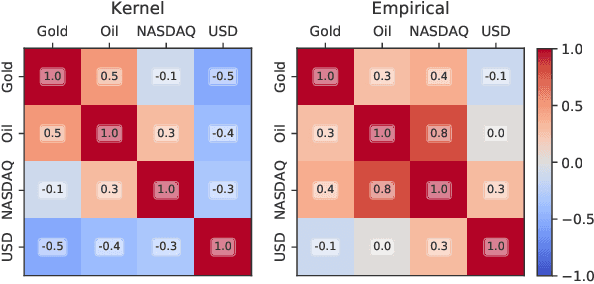
In Financial Signal Processing, multiple time series such as financial indicators, stock prices and exchange rates are strongly coupled due to their dependence on the latent state of the market and therefore they are required to be jointly analysed. We focus on learning the relationships among financial time series by modelling them through a multi-output Gaussian process (MOGP) with expressive covariance functions. Learning these market dependencies among financial series is crucial for the imputation and prediction of financial observations. The proposed model is validated experimentally on two real-world financial datasets for which their correlations across channels are analysed. We compare our model against other MOGPs and the independent Gaussian process on real financial data.

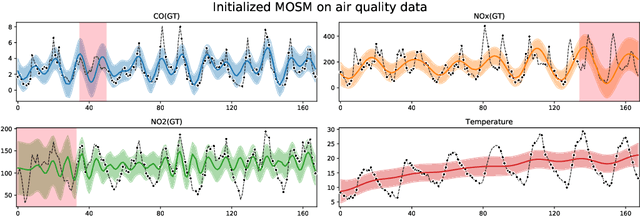
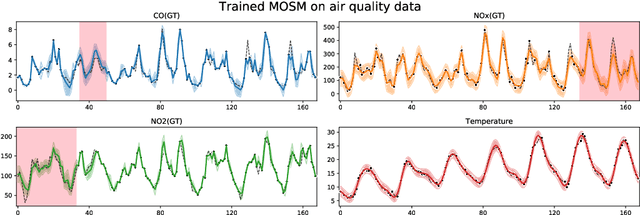
MOGPTK: The Multi-Output Gaussian Process Toolkit

We present MOGPTK, a Python package for multi-channel data modelling using Gaussian processes (GP). The aim of this toolkit is to make multi-output GP (MOGP) models accessible to researchers, data scientists, and practitioners alike. MOGPTK uses a Python front-end, relies on the GPflow suite and is built on a TensorFlow back-end, thus enabling GPU-accelerated training. The toolkit facilitates implementing the entire pipeline of GP modelling, including data loading, parameter initialization, model learning, parameter interpretation, up to data imputation and extrapolation. MOGPTK implements the main multi-output covariance kernels from literature, as well as spectral-based parameter initialization strategies. The source code, tutorials and examples in the form of Jupyter notebooks, together with the API documentation, can be found at http://github.com/GAMES-UChile/mogptk