MATATA: A weakly-supervised MAthematical Tool-Assisted reasoning for Tabular Applications

Mathematical reasoning capabilities are increasing with tool-augmented language agents, but methods often rely either on closed-source or large models, external data, or extensive prompt engineering. This work introduces MATATA, a novel cost-effective method to train LLM agents for tabular data problems through reasoning, planning, and tool use. With a progressive self-improvement paradigm and an iterative weak supervision, it empowers 3.8B/8B Small Language Models (SLMs), particularly suited for local hosting and sensitive business contexts where data privacy is crucial. By employing a flexible and reusable tools across different datasets, it achieves robust performance with effective scalability across shared tasks. Experiments show that MATATA reaches state-of-the-art performances on FinQA and TAT-QA among reasoning frameworks based on open-source models. Moreover, MATATA models compete with GPT-4 based frameworks on TabMWP, while being SLMs.

MATATA: a weak-supervised MAthematical Tool-Assisted reasoning for Tabular Applications

Mathematical reasoning capabilities are increasing with tool-augmented language agents, but methods often rely either on closed-source or large models, external data, or extensive prompt engineering. This work introduces MATATA, a novel cost-effective method to train LLM agents for tabular data problems through reasoning, planning, and tool use. With a progressive self-improvement paradigm and an iterative weak supervision, it empowers 3.8B/8B Small Language Models (SLMs), particularly suited for local hosting and sensitive business contexts where data privacy is crucial. By employing a flexible and reusable tools across different datasets, it achieves robust performance with effective scalability across shared tasks. Experiments show that MATATA reaches state-of-the-art performances on FinQA and TAT-QA among reasoning frameworks based on open-source models. Moreover, MATATA models compete with GPT-4 based frameworks on TabMWP, while being SLMs.

Towards Optimally Weighted Physics-Informed Neural Networks in Ocean Modelling

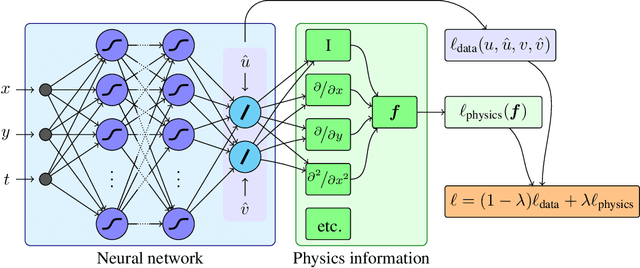
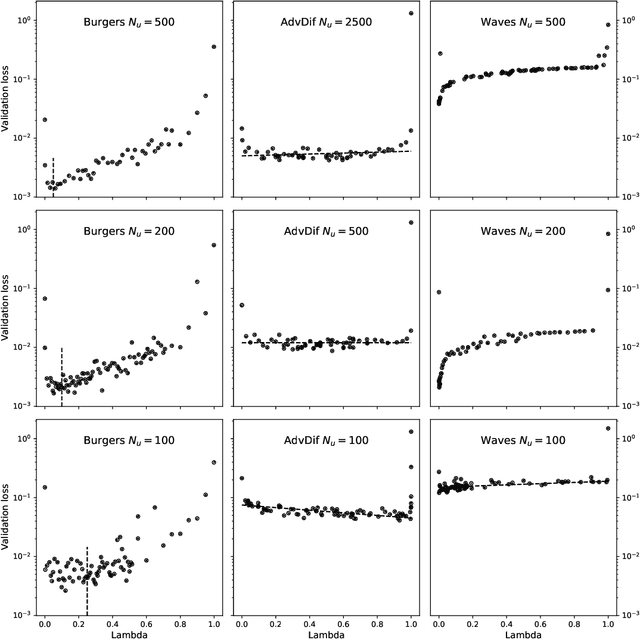
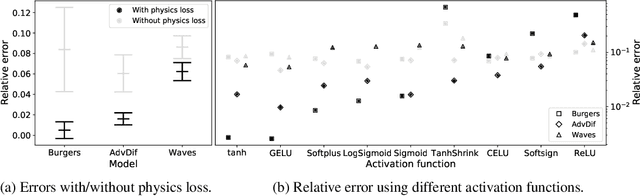
The carbon pump of the world's ocean plays a vital role in the biosphere and climate of the earth, urging improved understanding of the functions and influences of the ocean for climate change analyses. State-of-the-art techniques are required to develop models that can capture the complexity of ocean currents and temperature flows. This work explores the benefits of using physics-informed neural networks (PINNs) for solving partial differential equations related to ocean modeling; such as the Burgers, wave, and advection-diffusion equations. We explore the trade-offs of using data vs. physical models in PINNs for solving partial differential equations. PINNs account for the deviation from physical laws in order to improve learning and generalization. We observed how the relative weight between the data and physical model in the loss function influence training results, where small data sets benefit more from the added physics information.