Towards Optimally Weighted Physics-Informed Neural Networks in Ocean Modelling
Paper and Code
Jun 16, 2021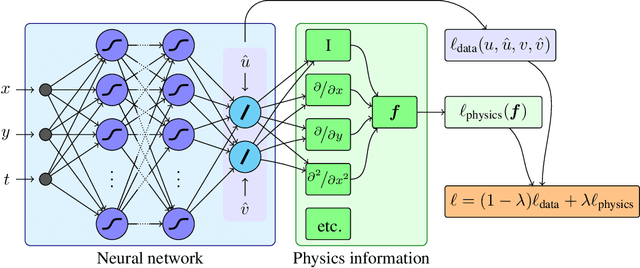

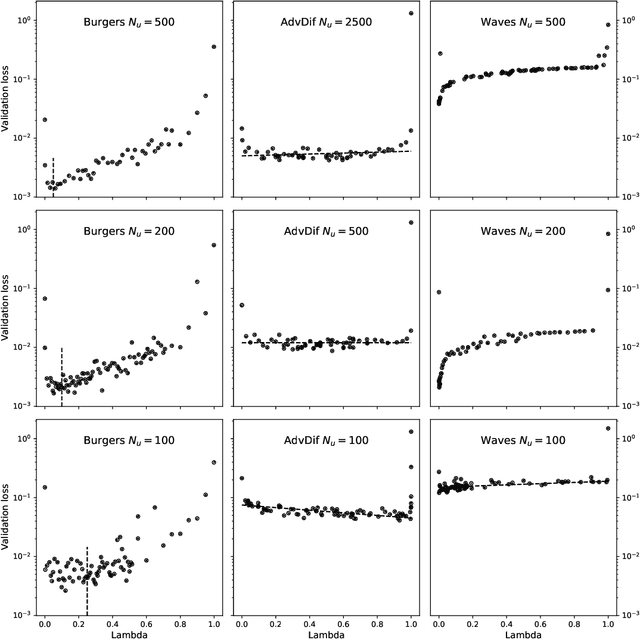
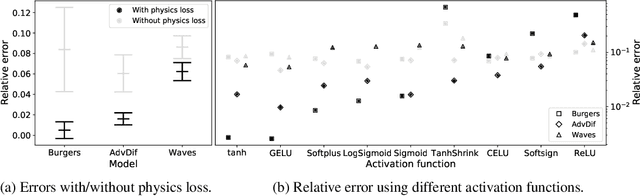
The carbon pump of the world's ocean plays a vital role in the biosphere and climate of the earth, urging improved understanding of the functions and influences of the ocean for climate change analyses. State-of-the-art techniques are required to develop models that can capture the complexity of ocean currents and temperature flows. This work explores the benefits of using physics-informed neural networks (PINNs) for solving partial differential equations related to ocean modeling; such as the Burgers, wave, and advection-diffusion equations. We explore the trade-offs of using data vs. physical models in PINNs for solving partial differential equations. PINNs account for the deviation from physical laws in order to improve learning and generalization. We observed how the relative weight between the data and physical model in the loss function influence training results, where small data sets benefit more from the added physics information.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge