Non-Asymptotic Analysis of Online Local Private Learning with SGD

Differentially Private Stochastic Gradient Descent (DP-SGD) has been widely used for solving optimization problems with privacy guarantees in machine learning and statistics. Despite this, a systematic non-asymptotic convergence analysis for DP-SGD, particularly in the context of online problems and local differential privacy (LDP) models, remains largely elusive. Existing non-asymptotic analyses have focused on non-private optimization methods, and hence are not applicable to privacy-preserving optimization problems. This work initiates the analysis to bridge this gap and opens the door to non-asymptotic convergence analysis of private optimization problems. A general framework is investigated for the online LDP model in stochastic optimization problems. We assume that sensitive information from individuals is collected sequentially and aim to estimate, in real-time, a static parameter that pertains to the population of interest. Most importantly, we conduct a comprehensive non-asymptotic convergence analysis of the proposed estimators in finite-sample situations, which gives their users practical guidelines regarding the effect of various hyperparameters, such as step size, parameter dimensions, and privacy budgets, on convergence rates. Our proposed estimators are validated in the theoretical and practical realms by rigorous mathematical derivations and carefully constructed numerical experiments.

Deep Fair Learning: A Unified Framework for Fine-tuning Representations with Sufficient Networks

Ensuring fairness in machine learning is a critical and challenging task, as biased data representations often lead to unfair predictions. To address this, we propose Deep Fair Learning, a framework that integrates nonlinear sufficient dimension reduction with deep learning to construct fair and informative representations. By introducing a novel penalty term during fine-tuning, our method enforces conditional independence between sensitive attributes and learned representations, addressing bias at its source while preserving predictive performance. Unlike prior methods, it supports diverse sensitive attributes, including continuous, discrete, binary, or multi-group types. Experiments on various types of data structure show that our approach achieves a superior balance between fairness and utility, significantly outperforming state-of-the-art baselines.

A Deep Bayesian Nonparametric Framework for Robust Mutual Information Estimation

Mutual Information (MI) is a crucial measure for capturing dependencies between variables, but exact computation is challenging in high dimensions with intractable likelihoods, impacting accuracy and robustness. One idea is to use an auxiliary neural network to train an MI estimator; however, methods based on the empirical distribution function (EDF) can introduce sharp fluctuations in the MI loss due to poor out-of-sample performance, destabilizing convergence. We present a Bayesian nonparametric (BNP) solution for training an MI estimator by constructing the MI loss with a finite representation of the Dirichlet process posterior to incorporate regularization in the training process. With this regularization, the MI loss integrates both prior knowledge and empirical data to reduce the loss sensitivity to fluctuations and outliers in the sample data, especially in small sample settings like mini-batches. This approach addresses the challenge of balancing accuracy and low variance by effectively reducing variance, leading to stabilized and robust MI loss gradients during training and enhancing the convergence of the MI approximation while offering stronger theoretical guarantees for convergence. We explore the application of our estimator in maximizing MI between the data space and the latent space of a variational autoencoder. Experimental results demonstrate significant improvements in convergence over EDF-based methods, with applications across synthetic and real datasets, notably in 3D CT image generation, yielding enhanced structure discovery and reduced overfitting in data synthesis. While this paper focuses on generative models in application, the proposed estimator is not restricted to this setting and can be applied more broadly in various BNP learning procedures.

Evaluation of OpenAI o1: Opportunities and Challenges of AGI

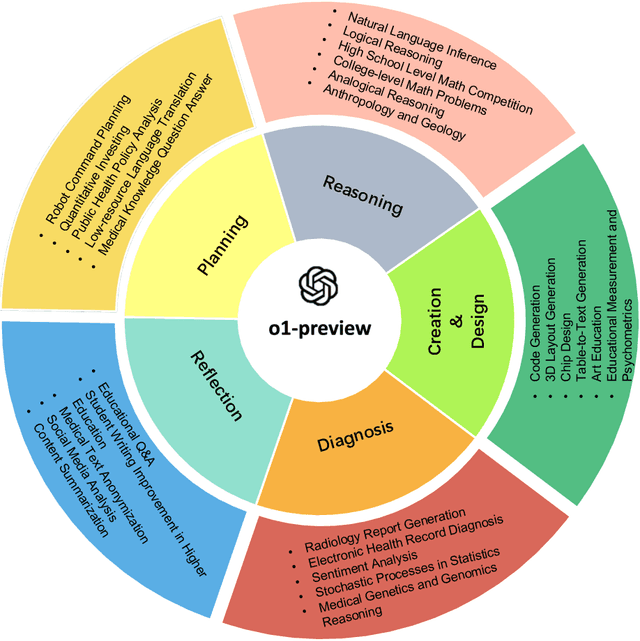
This comprehensive study evaluates the performance of OpenAI's o1-preview large language model across a diverse array of complex reasoning tasks, spanning multiple domains, including computer science, mathematics, natural sciences, medicine, linguistics, and social sciences. Through rigorous testing, o1-preview demonstrated remarkable capabilities, often achieving human-level or superior performance in areas ranging from coding challenges to scientific reasoning and from language processing to creative problem-solving. Key findings include: -83.3% success rate in solving complex competitive programming problems, surpassing many human experts. -Superior ability in generating coherent and accurate radiology reports, outperforming other evaluated models. -100% accuracy in high school-level mathematical reasoning tasks, providing detailed step-by-step solutions. -Advanced natural language inference capabilities across general and specialized domains like medicine. -Impressive performance in chip design tasks, outperforming specialized models in areas such as EDA script generation and bug analysis. -Remarkable proficiency in anthropology and geology, demonstrating deep understanding and reasoning in these specialized fields. -Strong capabilities in quantitative investing. O1 has comprehensive financial knowledge and statistical modeling skills. -Effective performance in social media analysis, including sentiment analysis and emotion recognition. The model excelled particularly in tasks requiring intricate reasoning and knowledge integration across various fields. While some limitations were observed, including occasional errors on simpler problems and challenges with certain highly specialized concepts, the overall results indicate significant progress towards artificial general intelligence.

Oblivious subspace embeddings for compressed Tucker decompositions

Emphasis in the tensor literature on random embeddings (tools for low-distortion dimension reduction) for the canonical polyadic (CP) tensor decomposition has left analogous results for the more expressive Tucker decomposition comparatively lacking. This work establishes general Johnson-Lindenstrauss (JL) type guarantees for the estimation of Tucker decompositions when an oblivious random embedding is applied along each mode. When these embeddings are drawn from a JL-optimal family, the decomposition can be estimated within $\varepsilon$ relative error under restrictions on the embedding dimension that are in line with recent CP results. We implement a higher-order orthogonal iteration (HOOI) decomposition algorithm with random embeddings to demonstrate the practical benefits of this approach and its potential to improve the accessibility of otherwise prohibitive tensor analyses. On moderately large face image and fMRI neuroimaging datasets, empirical results show that substantial dimension reduction is possible with minimal increase in reconstruction error relative to traditional HOOI ($\leq$5% larger error, 50%-60% lower computation time for large models with 50% dimension reduction along each mode). Especially for large tensors, our method outperforms traditional higher-order singular value decomposition (HOSVD) and recently proposed TensorSketch methods.

Gaussian Differential Privacy on Riemannian Manifolds

We develop an advanced approach for extending Gaussian Differential Privacy (GDP) to general Riemannian manifolds. The concept of GDP stands out as a prominent privacy definition that strongly warrants extension to manifold settings, due to its central limit properties. By harnessing the power of the renowned Bishop-Gromov theorem in geometric analysis, we propose a Riemannian Gaussian distribution that integrates the Riemannian distance, allowing us to achieve GDP in Riemannian manifolds with bounded Ricci curvature. To the best of our knowledge, this work marks the first instance of extending the GDP framework to accommodate general Riemannian manifolds, encompassing curved spaces, and circumventing the reliance on tangent space summaries. We provide a simple algorithm to evaluate the privacy budget $\mu$ on any one-dimensional manifold and introduce a versatile Markov Chain Monte Carlo (MCMC)-based algorithm to calculate $\mu$ on any Riemannian manifold with constant curvature. Through simulations on one of the most prevalent manifolds in statistics, the unit sphere $S^d$, we demonstrate the superior utility of our Riemannian Gaussian mechanism in comparison to the previously proposed Riemannian Laplace mechanism for implementing GDP.

Class Interference of Deep Neural Networks

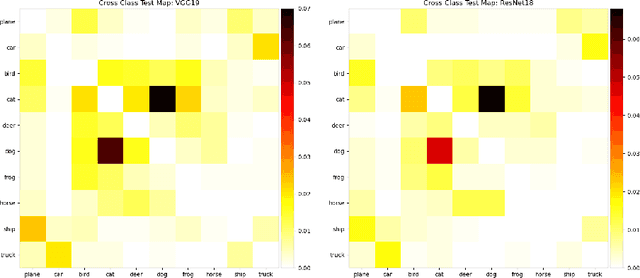
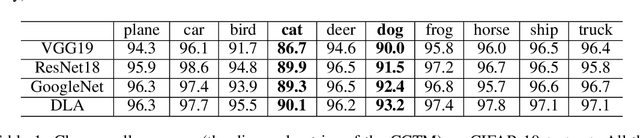
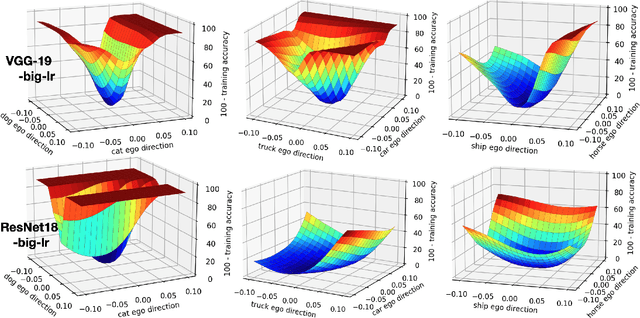
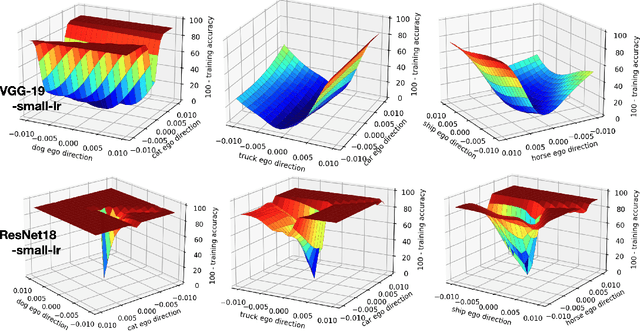
Recognizing and telling similar objects apart is even hard for human beings. In this paper, we show that there is a phenomenon of class interference with all deep neural networks. Class interference represents the learning difficulty in data, and it constitutes the largest percentage of generalization errors by deep networks. To understand class interference, we propose cross-class tests, class ego directions and interference models. We show how to use these definitions to study minima flatness and class interference of a trained model. We also show how to detect class interference during training through label dancing pattern and class dancing notes.

Conformalized Fairness via Quantile Regression

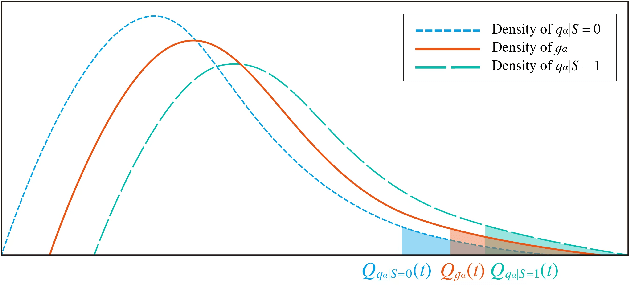
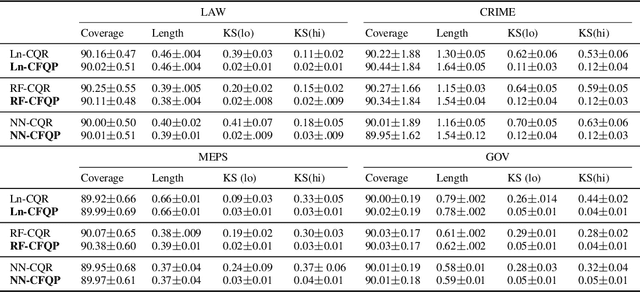
Algorithmic fairness has received increased attention in socially sensitive domains. While rich literature on mean fairness has been established, research on quantile fairness remains sparse but vital. To fulfill great needs and advocate the significance of quantile fairness, we propose a novel framework to learn a real-valued quantile function under the fairness requirement of Demographic Parity with respect to sensitive attributes, such as race or gender, and thereby derive a reliable fair prediction interval. Using optimal transport and functional synchronization techniques, we establish theoretical guarantees of distribution-free coverage and exact fairness for the induced prediction interval constructed by fair quantiles. A hands-on pipeline is provided to incorporate flexible quantile regressions with an efficient fairness adjustment post-processing algorithm. We demonstrate the superior empirical performance of this approach on several benchmark datasets. Our results show the model's ability to uncover the mechanism underlying the fairness-accuracy trade-off in a wide range of societal and medical applications.

How Does Value Distribution in Distributional Reinforcement Learning Help Optimization?

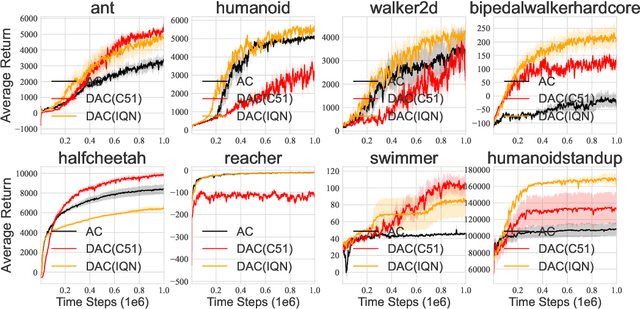
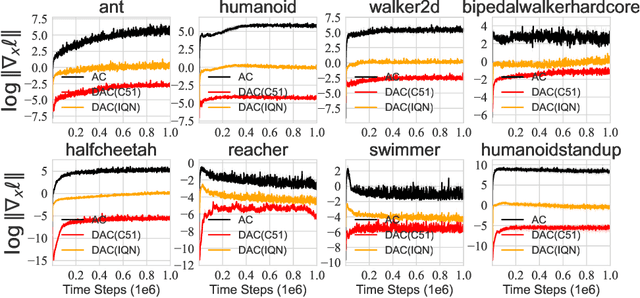
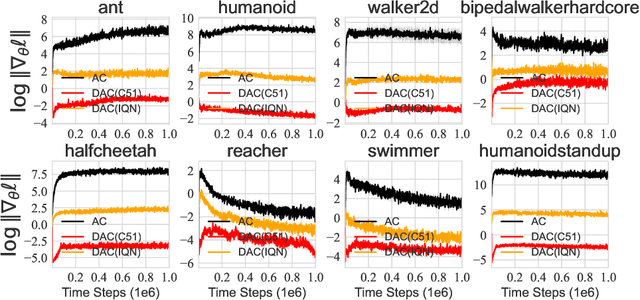
We consider the problem of learning a set of probability distributions from the Bellman dynamics in distributional reinforcement learning~(RL) that learns the whole return distribution compared with only its expectation in classical RL. Despite its success to obtain superior performance, we still have a poor understanding of how the value distribution in distributional RL works. In this study, we analyze the optimization benefits of distributional RL by leverage of additional value distribution information over classical RL in the Neural Fitted Z-Iteration~(Neural FZI) framework. To begin with, we demonstrate that the distribution loss of distributional RL has desirable smoothness characteristics and hence enjoys stable gradients, which is in line with its tendency to promote optimization stability. Furthermore, the acceleration effect of distributional RL is revealed by decomposing the return distribution. It turns out that distributional RL can perform favorably if the value distribution approximation is appropriate, measured by the variance of gradient estimates in each environment for any specific distributional RL algorithm. Rigorous experiments validate the stable optimization behaviors of distributional RL, contributing to its acceleration effects compared to classical RL. The findings of our research illuminate how the value distribution in distributional RL algorithms helps the optimization.

Sigmoidally Preconditioned Off-policy Learning:a new exploration method for reinforcement learning

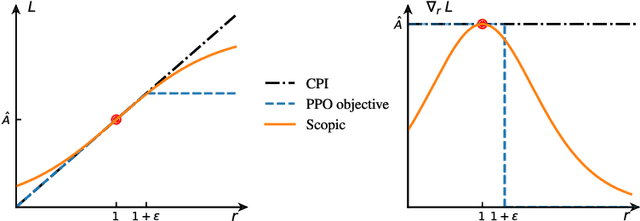
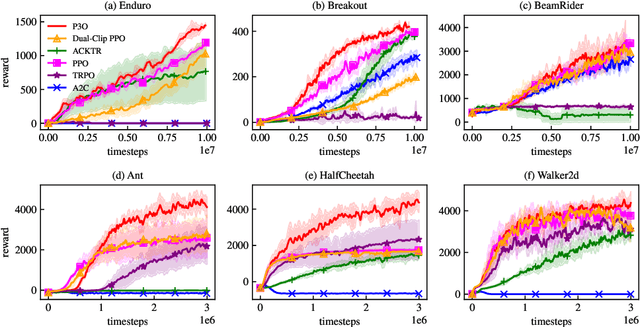
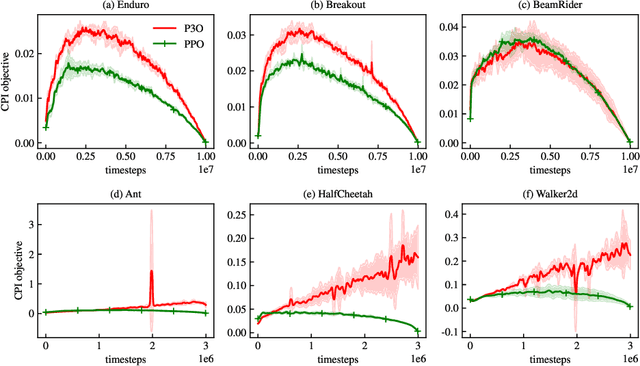
One of the major difficulties of reinforcement learning is learning from {\em off-policy} samples, which are collected by a different policy (behavior policy) from what the algorithm evaluates (the target policy). Off-policy learning needs to correct the distribution of the samples from the behavior policy towards that of the target policy. Unfortunately, important sampling has an inherent high variance issue which leads to poor gradient estimation in policy gradient methods. We focus on an off-policy Actor-Critic architecture, and propose a novel method, called Preconditioned Proximal Policy Optimization (P3O), which can control the high variance of importance sampling by applying a preconditioner to the Conservative Policy Iteration (CPI) objective. {\em This preconditioning uses the sigmoid function in a special way that when there is no policy change, the gradient is maximal and hence policy gradient will drive a big parameter update for an efficient exploration of the parameter space}. This is a novel exploration method that has not been studied before given that existing exploration methods are based on the novelty of states and actions. We compare with several best-performing algorithms on both discrete and continuous tasks and the results confirmed that {\em P3O is more off-policy than PPO} according to the "off-policyness" measured by the DEON metric, and P3O explores in a larger policy space than PPO. Results also show that our P3O maximizes the CPI objective better than PPO during the training process.