Yingnan Zhao
MoRE: Mixture of Residual Experts for Humanoid Lifelike Gaits Learning on Complex Terrains
Jun 12, 2025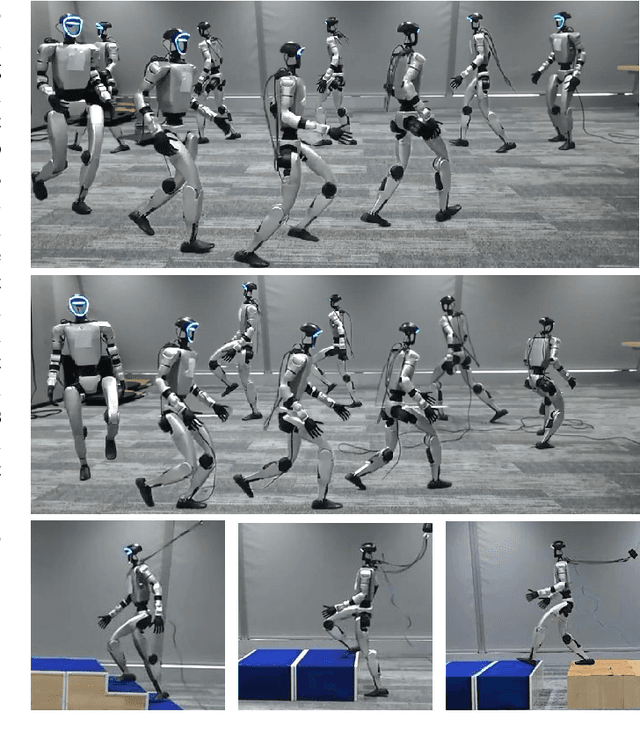
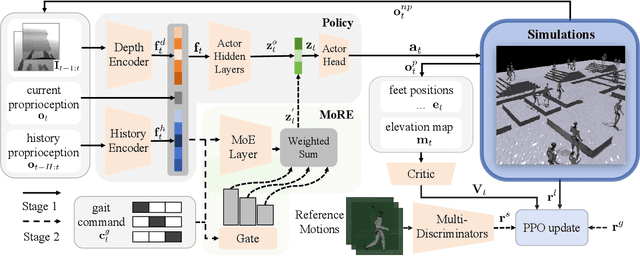
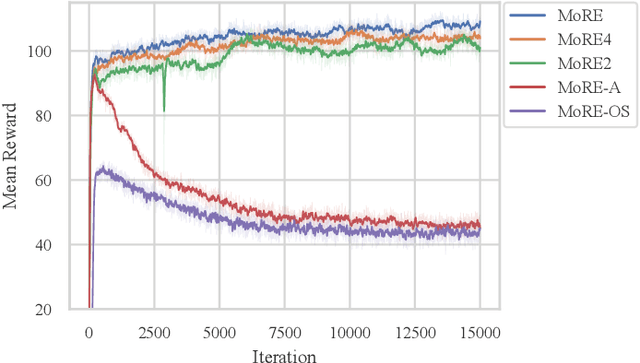
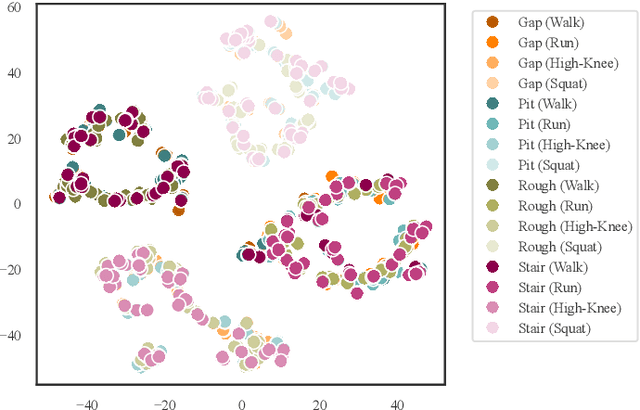
Abstract:Humanoid robots have demonstrated robust locomotion capabilities using Reinforcement Learning (RL)-based approaches. Further, to obtain human-like behaviors, existing methods integrate human motion-tracking or motion prior in the RL framework. However, these methods are limited in flat terrains with proprioception only, restricting their abilities to traverse challenging terrains with human-like gaits. In this work, we propose a novel framework using a mixture of latent residual experts with multi-discriminators to train an RL policy, which is capable of traversing complex terrains in controllable lifelike gaits with exteroception. Our two-stage training pipeline first teaches the policy to traverse complex terrains using a depth camera, and then enables gait-commanded switching between human-like gait patterns. We also design gait rewards to adjust human-like behaviors like robot base height. Simulation and real-world experiments demonstrate that our framework exhibits exceptional performance in traversing complex terrains, and achieves seamless transitions between multiple human-like gait patterns.
An Imitative Reinforcement Learning Framework for Autonomous Dogfight
Jun 17, 2024Abstract:Unmanned Combat Aerial Vehicle (UCAV) dogfight, which refers to a fight between two or more UCAVs usually at close quarters, plays a decisive role on the aerial battlefields. With the evolution of artificial intelligence, dogfight progressively transits towards intelligent and autonomous modes. However, the development of autonomous dogfight policy learning is hindered by challenges such as weak exploration capabilities, low learning efficiency, and unrealistic simulated environments. To overcome these challenges, this paper proposes a novel imitative reinforcement learning framework, which efficiently leverages expert data while enabling autonomous exploration. The proposed framework not only enhances learning efficiency through expert imitation, but also ensures adaptability to dynamic environments via autonomous exploration with reinforcement learning. Therefore, the proposed framework can learn a successful dogfight policy of 'pursuit-lock-launch' for UCAVs. To support data-driven learning, we establish a dogfight environment based on the Harfang3D sandbox, where we conduct extensive experiments. The results indicate that the proposed framework excels in multistage dogfight, significantly outperforms state-of-the-art reinforcement learning and imitation learning methods. Thanks to the ability of imitating experts and autonomous exploration, our framework can quickly learn the critical knowledge in complex aerial combat tasks, achieving up to a 100% success rate and demonstrating excellent robustness.
Auxiliary Reward Generation with Transition Distance Representation Learning
Feb 12, 2024



Abstract:Reinforcement learning (RL) has shown its strength in challenging sequential decision-making problems. The reward function in RL is crucial to the learning performance, as it serves as a measure of the task completion degree. In real-world problems, the rewards are predominantly human-designed, which requires laborious tuning, and is easily affected by human cognitive biases. To achieve automatic auxiliary reward generation, we propose a novel representation learning approach that can measure the ``transition distance'' between states. Building upon these representations, we introduce an auxiliary reward generation technique for both single-task and skill-chaining scenarios without the need for human knowledge. The proposed approach is evaluated in a wide range of manipulation tasks. The experiment results demonstrate the effectiveness of measuring the transition distance between states and the induced improvement by auxiliary rewards, which not only promotes better learning efficiency but also increases convergent stability.
Distributional Reinforcement Learning via Sinkhorn Iterations
Feb 16, 2022
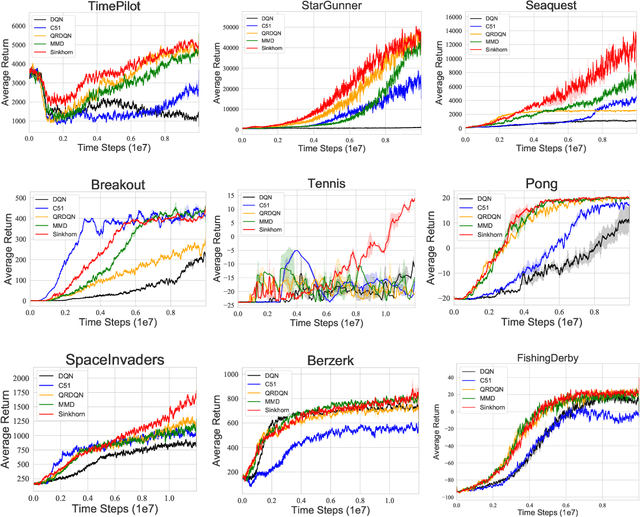
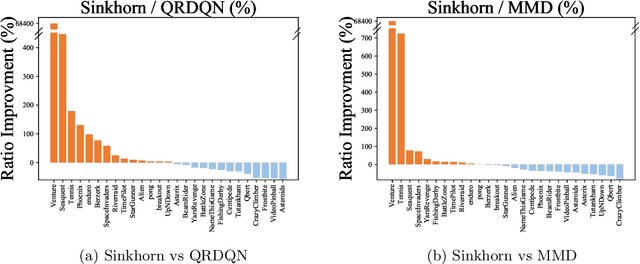
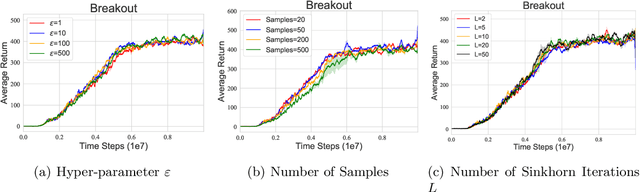
Abstract:Distributional reinforcement learning~(RL) is a class of state-of-the-art algorithms that estimate the whole distribution of the total return rather than only its expectation. The representation manner of each return distribution and the choice of distribution divergence are pivotal for the empirical success of distributional RL. In this paper, we propose a new class of \textit{Sinkhorn distributional RL} algorithm that learns a finite set of statistics, i.e., deterministic samples, from each return distribution and then leverages Sinkhorn iterations to evaluate the Sinkhorn distance between the current and target Bellmen distributions. Remarkably, as Sinkhorn divergence interpolates between the Wasserstein distance and Maximum Mean Discrepancy~(MMD). This allows our proposed Sinkhorn distributional RL algorithms to find a sweet spot leveraging the geometry of optimal transport-based distance, and the unbiased gradient estimates of MMD. Finally, experiments on a suite of Atari games reveal the competitive performance of Sinkhorn distributional RL algorithm as opposed to existing state-of-the-art algorithms.
Damped Anderson Mixing for Deep Reinforcement Learning: Acceleration, Convergence, and Stabilization
Oct 20, 2021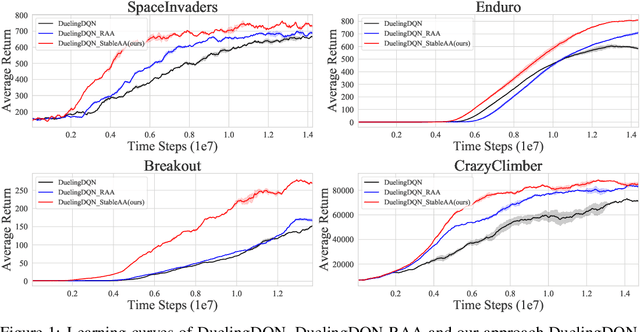
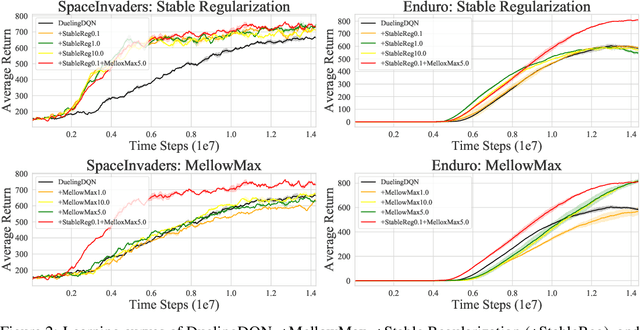
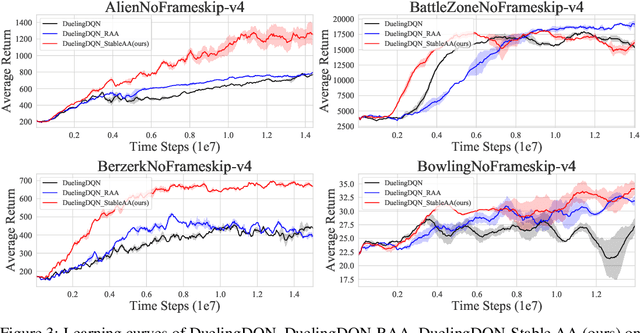
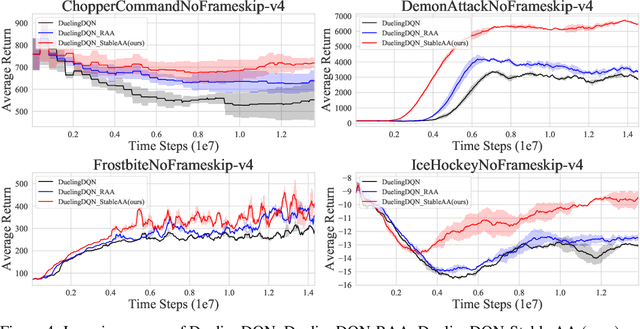
Abstract:Anderson mixing has been heuristically applied to reinforcement learning (RL) algorithms for accelerating convergence and improving the sampling efficiency of deep RL. Despite its heuristic improvement of convergence, a rigorous mathematical justification for the benefits of Anderson mixing in RL has not yet been put forward. In this paper, we provide deeper insights into a class of acceleration schemes built on Anderson mixing that improve the convergence of deep RL algorithms. Our main results establish a connection between Anderson mixing and quasi-Newton methods and prove that Anderson mixing increases the convergence radius of policy iteration schemes by an extra contraction factor. The key focus of the analysis roots in the fixed-point iteration nature of RL. We further propose a stabilization strategy by introducing a stable regularization term in Anderson mixing and a differentiable, non-expansive MellowMax operator that can allow both faster convergence and more stable behavior. Extensive experiments demonstrate that our proposed method enhances the convergence, stability, and performance of RL algorithms.
Towards Understanding Distributional Reinforcement Learning: Regularization, Optimization, Acceleration and Sinkhorn Algorithm
Oct 07, 2021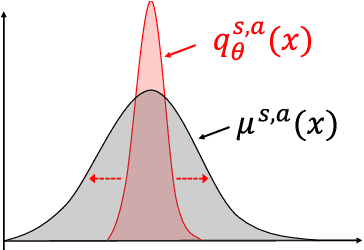
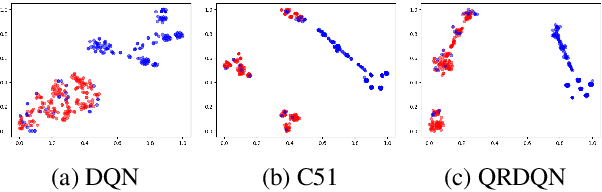
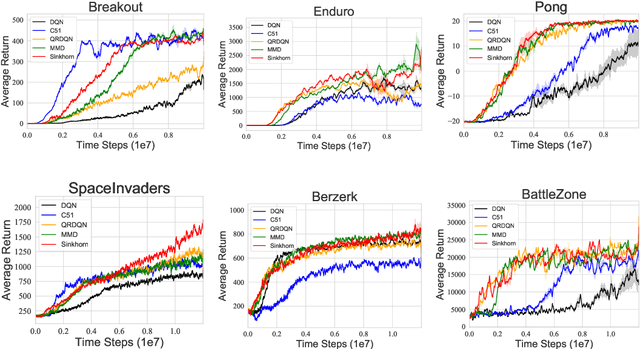
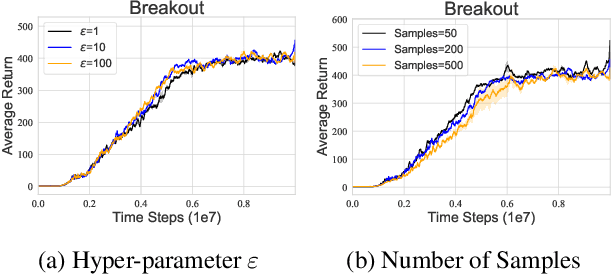
Abstract:Distributional reinforcement learning~(RL) is a class of state-of-the-art algorithms that estimate the whole distribution of the total return rather than only its expectation. Despite the remarkable performance of distributional RL, a theoretical understanding of its advantages over expectation-based RL remains elusive. In this paper, we interpret distributional RL as entropy-regularized maximum likelihood estimation in the \textit{neural Z-fitted iteration} framework, and establish the connection of the resulting risk-aware regularization with maximum entropy RL. In addition, We shed light on the stability-promoting distributional loss with desirable smoothness properties in distributional RL, which can yield stable optimization and guaranteed generalization. We also analyze the acceleration behavior while optimizing distributional RL algorithms and show that an appropriate approximation to the true target distribution can speed up the convergence. From the perspective of representation, we find that distributional RL encourages state representation from the same action class classified by the policy in tighter clusters. Finally, we propose a class of \textit{Sinkhorn distributional RL} algorithm that interpolates between the Wasserstein distance and maximum mean discrepancy~(MMD). Experiments on a suite of Atari games reveal the competitive performance of our algorithm relative to existing state-of-the-art distributional RL algorithms.
Exploring the Robustness of Distributional Reinforcement Learning against Noisy State Observations
Sep 17, 2021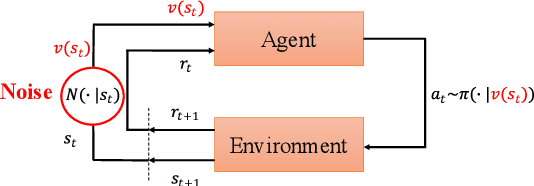
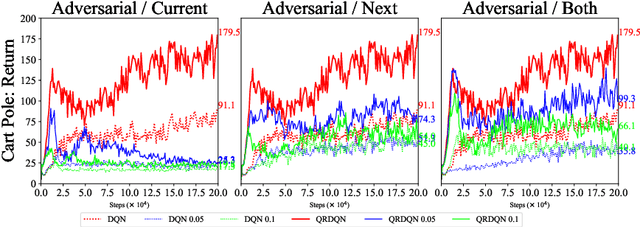
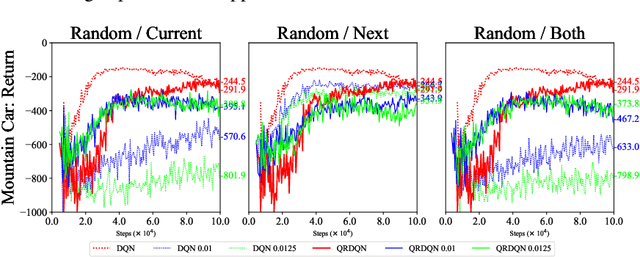
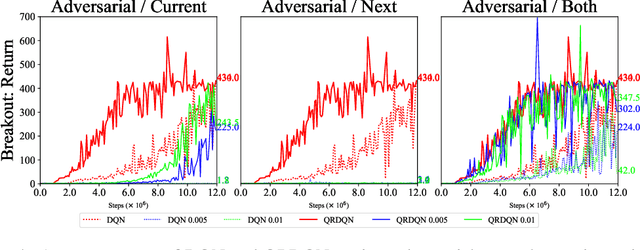
Abstract:In real scenarios, state observations that an agent observes may contain measurement errors or adversarial noises, misleading the agent to take suboptimal actions or even collapse while training. In this paper, we study the training robustness of distributional Reinforcement Learning~(RL), a class of state-of-the-art methods that estimate the whole distribution, as opposed to only the expectation, of the total return. Firstly, we propose State-Noisy Markov Decision Process~(SN-MDP) in the tabular case to incorporate both random and adversarial state observation noises, in which the contraction of both expectation-based and distributional Bellman operators is derived. Beyond SN-MDP with the function approximation, we theoretically characterize the bounded gradient norm of histogram-based distributional loss, accounting for the better training robustness of distribution RL. We also provide stricter convergence conditions of the Temporal-Difference~(TD) learning under more flexible state noises, as well as the sensitivity analysis by the leverage of influence function. Finally, extensive experiments on the suite of games show that distributional RL enjoys better training robustness compared with its expectation-based counterpart across various state observation noises.
Variational Dynamic for Self-Supervised Exploration in Deep Reinforcement Learning
Oct 17, 2020
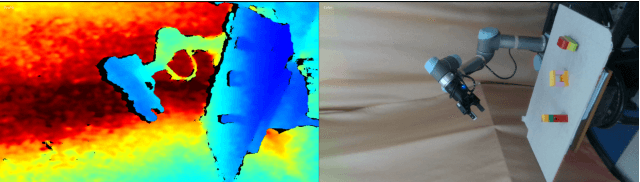
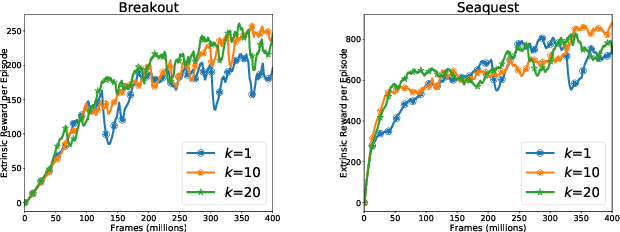
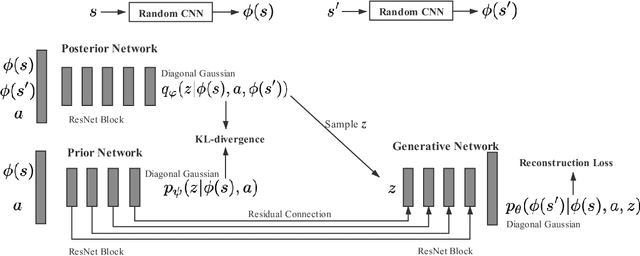
Abstract:Efficient exploration remains a challenging problem in reinforcement learning, especially for tasks where extrinsic rewards from environments are sparse or even totally disregarded. Significant advances based on intrinsic motivation show promising results in simple environments but often get stuck in environments with multimodal and stochastic dynamics. In this work, we propose a variational dynamic model based on the conditional variational inference to model the multimodality and stochasticity. We consider the environmental state-action transition as a conditional generative process by generating the next-state prediction under the condition of the current state, action, and latent variable. We derive an upper bound of the negative log-likelihood of the environmental transition and use such an upper bound as the intrinsic reward for exploration, which allows the agent to learn skills by self-supervised exploration without observing extrinsic rewards. We evaluate the proposed method on several image-based simulation tasks and a real robotic manipulating task. Our method outperforms several state-of-the-art environment model-based exploration approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge