DRGCN: Dynamic Evolving Initial Residual for Deep Graph Convolutional Networks

Graph convolutional networks (GCNs) have been proved to be very practical to handle various graph-related tasks. It has attracted considerable research interest to study deep GCNs, due to their potential superior performance compared with shallow ones. However, simply increasing network depth will, on the contrary, hurt the performance due to the over-smoothing problem. Adding residual connection is proved to be effective for learning deep convolutional neural networks (deep CNNs), it is not trivial when applied to deep GCNs. Recent works proposed an initial residual mechanism that did alleviate the over-smoothing problem in deep GCNs. However, according to our study, their algorithms are quite sensitive to different datasets. In their setting, the personalization (dynamic) and correlation (evolving) of how residual applies are ignored. To this end, we propose a novel model called Dynamic evolving initial Residual Graph Convolutional Network (DRGCN). Firstly, we use a dynamic block for each node to adaptively fetch information from the initial representation. Secondly, we use an evolving block to model the residual evolving pattern between layers. Our experimental results show that our model effectively relieves the problem of over-smoothing in deep GCNs and outperforms the state-of-the-art (SOTA) methods on various benchmark datasets. Moreover, we develop a mini-batch version of DRGCN which can be applied to large-scale data. Coupling with several fair training techniques, our model reaches new SOTA results on the large-scale ogbn-arxiv dataset of Open Graph Benchmark (OGB). Our reproducible code is available on GitHub.

Towards Understanding Distributional Reinforcement Learning: Regularization, Optimization, Acceleration and Sinkhorn Algorithm

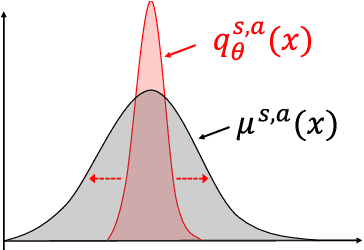
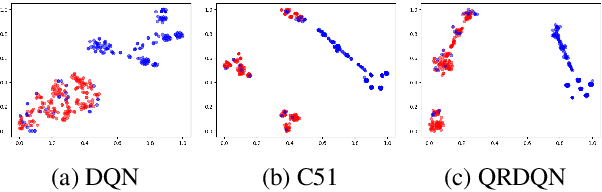
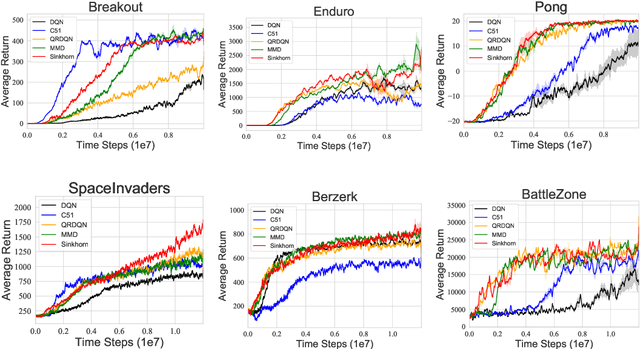
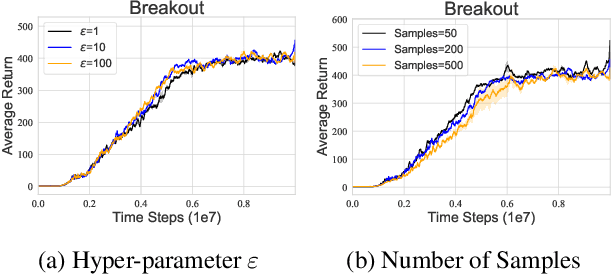
Distributional reinforcement learning~(RL) is a class of state-of-the-art algorithms that estimate the whole distribution of the total return rather than only its expectation. Despite the remarkable performance of distributional RL, a theoretical understanding of its advantages over expectation-based RL remains elusive. In this paper, we interpret distributional RL as entropy-regularized maximum likelihood estimation in the \textit{neural Z-fitted iteration} framework, and establish the connection of the resulting risk-aware regularization with maximum entropy RL. In addition, We shed light on the stability-promoting distributional loss with desirable smoothness properties in distributional RL, which can yield stable optimization and guaranteed generalization. We also analyze the acceleration behavior while optimizing distributional RL algorithms and show that an appropriate approximation to the true target distribution can speed up the convergence. From the perspective of representation, we find that distributional RL encourages state representation from the same action class classified by the policy in tighter clusters. Finally, we propose a class of \textit{Sinkhorn distributional RL} algorithm that interpolates between the Wasserstein distance and maximum mean discrepancy~(MMD). Experiments on a suite of Atari games reveal the competitive performance of our algorithm relative to existing state-of-the-art distributional RL algorithms.