Baird Counterexample is Solved: with an example of How to Debug a Two-time-scale Algorithm

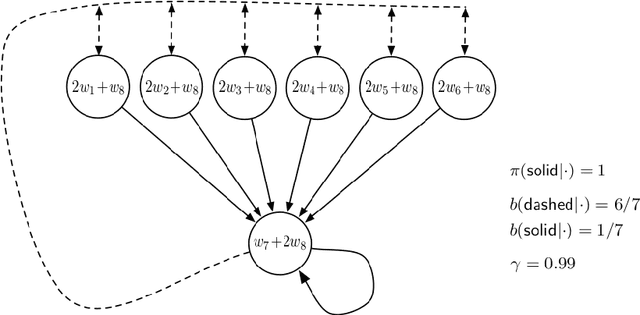
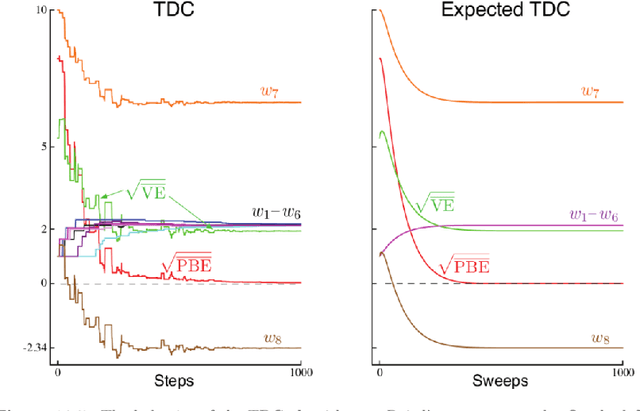
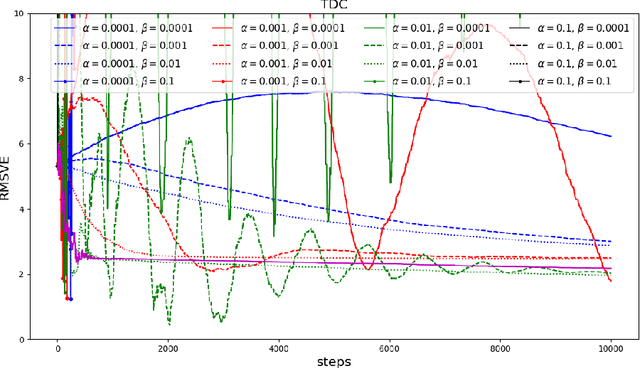
Baird counterexample was proposed by Leemon Baird in 1995, first used to show that the Temporal Difference (TD(0)) algorithm diverges on this example. Since then, it is often used to test and compare off-policy learning algorithms. Gradient TD algorithms solved the divergence issue of TD on Baird counterexample. However, their convergence on this example is still very slow, and the nature of the slowness is not well understood, e.g., see (Sutton and Barto 2018). This note is to understand in particular, why TDC is slow on this example, and provide a debugging analysis to understand this behavior. Our debugging technique can be used to study the convergence behavior of two-time-scale stochastic approximation algorithms. We also provide empirical results of the recent Impression GTD algorithm on this example, showing the convergence is very fast, in fact, in a linear rate. We conclude that Baird counterexample is solved, by an algorithm with the convergence guarantee to the TD solution in general, and a fast convergence rate.

Careful at Estimation and Bold at Exploration

Exploration strategies in continuous action space are often heuristic due to the infinite actions, and these kinds of methods cannot derive a general conclusion. In prior work, it has been shown that policy-based exploration is beneficial for continuous action space in deterministic policy reinforcement learning(DPRL). However, policy-based exploration in DPRL has two prominent issues: aimless exploration and policy divergence, and the policy gradient for exploration is only sometimes helpful due to inaccurate estimation. Based on the double-Q function framework, we introduce a novel exploration strategy to mitigate these issues, separate from the policy gradient. We first propose the greedy Q softmax update schema for Q value update. The expected Q value is derived by weighted summing the conservative Q value over actions, and the weight is the corresponding greedy Q value. Greedy Q takes the maximum value of the two Q functions, and conservative Q takes the minimum value of the two different Q functions. For practicality, this theoretical basis is then extended to allow us to combine action exploration with the Q value update, except for the premise that we have a surrogate policy that behaves like this exploration policy. In practice, we construct such an exploration policy with a few sampled actions, and to meet the premise, we learn such a surrogate policy by minimizing the KL divergence between the target policy and the exploration policy constructed by the conservative Q. We evaluate our method on the Mujoco benchmark and demonstrate superior performance compared to previous state-of-the-art methods across various environments, particularly in the most complex Humanoid environment.

A new Gradient TD Algorithm with only One Step-size: Convergence Rate Analysis using $L$-$λ$ Smoothness

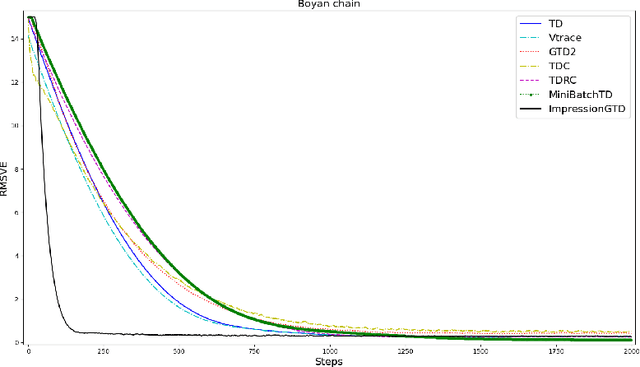
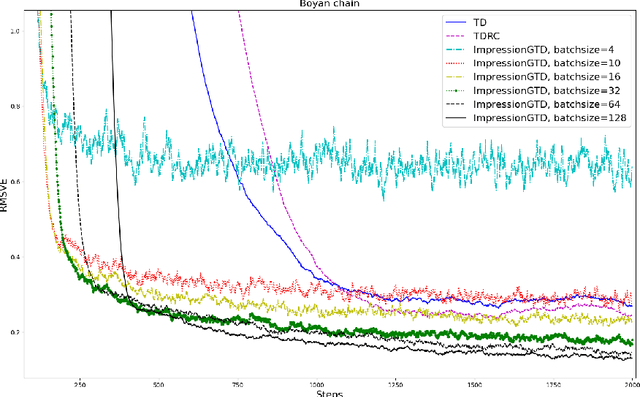
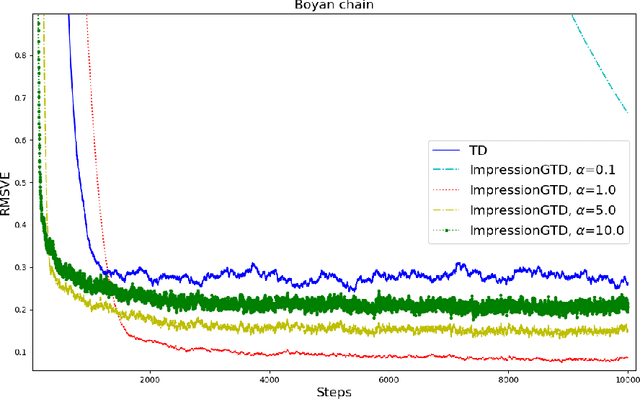
Gradient Temporal Difference (GTD) algorithms (Sutton et al., 2008, 2009) are the first $O(d)$ ($d$ is the number features) algorithms that have convergence guarantees for off-policy learning with linear function approximation. Liu et al. (2015) and Dalal et. al. (2018) proved the convergence rates of GTD, GTD2 and TDC are $O(t^{-\alpha/2})$ for some $\alpha \in (0,1)$. This bound is tight (Dalal et al., 2020), and slower than $O(1/\sqrt{t})$. GTD algorithms also have two step-size parameters, which are difficult to tune. In literature, there is a "single-time-scale" formulation of GTD. However, this formulation still has two step-size parameters. This paper presents a truly single-time-scale GTD algorithm for minimizing the Norm of Expected td Update (NEU) objective, and it has only one step-size parameter. We prove that the new algorithm, called Impression GTD, converges at least as fast as $O(1/t)$. Furthermore, based on a generalization of the expected smoothness (Gower et al. 2019), called $L$-$\lambda$ smoothness, we are able to prove that the new GTD converges even faster, in fact, with a linear rate. Our rate actually also improves Gower et al.'s result with a tighter bound under a weaker assumption. Besides Impression GTD, we also prove the rates of three other GTD algorithms, one by Yao and Liu (2008), another called A-transpose-TD (Sutton et al., 2008), and a counterpart of A-transpose-TD. The convergence rates of all the four GTD algorithms are proved in a single generic GTD framework to which $L$-$\lambda$ smoothness applies. Empirical results on Random walks, Boyan chain, and Baird counterexample show that Impression GTD converges much faster than existing GTD algorithms for both on-policy and off-policy learning problems, with well-performing step-sizes in a big range.

The Vanishing Decision Boundary Complexity and the Strong First Component

We show that unlike machine learning classifiers, there are no complex boundary structures in the decision boundaries for well-trained deep models. However, we found that the complicated structures do appear in training but they vanish shortly after shaping. This is a pessimistic news if one seeks to capture different levels of complexity in the decision boundary for understanding generalization, which works well in machine learning. Nonetheless, we found that the decision boundaries of predecessor models on the training data are reflective of the final model's generalization. We show how to use the predecessor decision boundaries for studying the generalization of deep models. We have three major findings. One is on the strength of the first principle component of deep models, another about the singularity of optimizers, and the other on the effects of the skip connections in ResNets. Code is at https://github.com/hengshu1/decision_boundary_github.

Class Interference of Deep Neural Networks

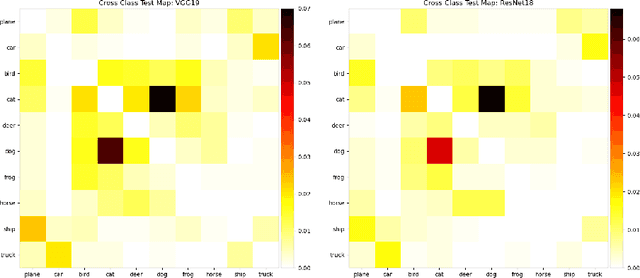
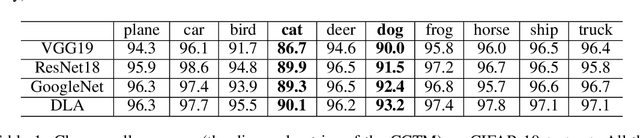
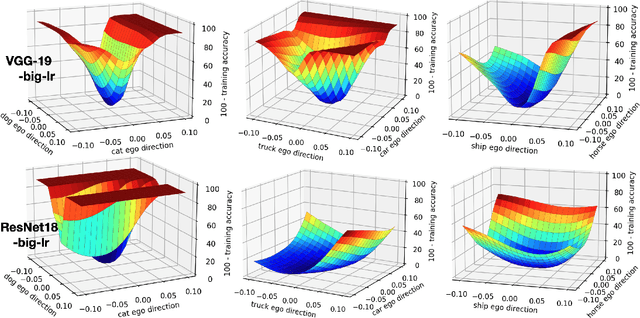
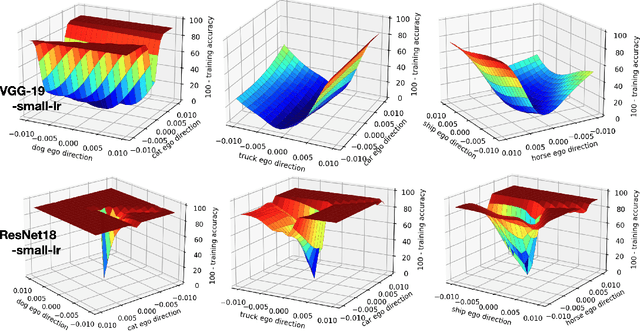
Recognizing and telling similar objects apart is even hard for human beings. In this paper, we show that there is a phenomenon of class interference with all deep neural networks. Class interference represents the learning difficulty in data, and it constitutes the largest percentage of generalization errors by deep networks. To understand class interference, we propose cross-class tests, class ego directions and interference models. We show how to use these definitions to study minima flatness and class interference of a trained model. We also show how to detect class interference during training through label dancing pattern and class dancing notes.

Sigmoidally Preconditioned Off-policy Learning:a new exploration method for reinforcement learning

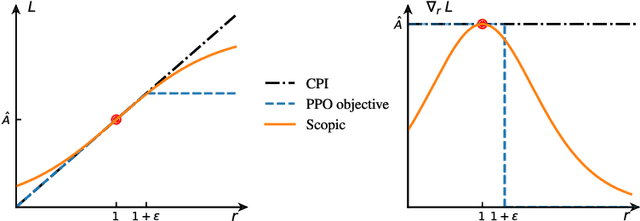
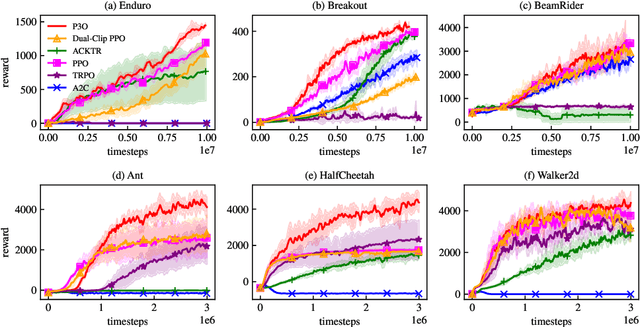
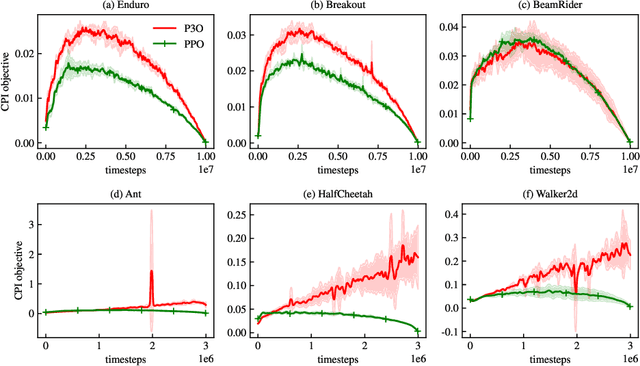
One of the major difficulties of reinforcement learning is learning from {\em off-policy} samples, which are collected by a different policy (behavior policy) from what the algorithm evaluates (the target policy). Off-policy learning needs to correct the distribution of the samples from the behavior policy towards that of the target policy. Unfortunately, important sampling has an inherent high variance issue which leads to poor gradient estimation in policy gradient methods. We focus on an off-policy Actor-Critic architecture, and propose a novel method, called Preconditioned Proximal Policy Optimization (P3O), which can control the high variance of importance sampling by applying a preconditioner to the Conservative Policy Iteration (CPI) objective. {\em This preconditioning uses the sigmoid function in a special way that when there is no policy change, the gradient is maximal and hence policy gradient will drive a big parameter update for an efficient exploration of the parameter space}. This is a novel exploration method that has not been studied before given that existing exploration methods are based on the novelty of states and actions. We compare with several best-performing algorithms on both discrete and continuous tasks and the results confirmed that {\em P3O is more off-policy than PPO} according to the "off-policyness" measured by the DEON metric, and P3O explores in a larger policy space than PPO. Results also show that our P3O maximizes the CPI objective better than PPO during the training process.

Learning to Accelerate by the Methods of Step-size Planning

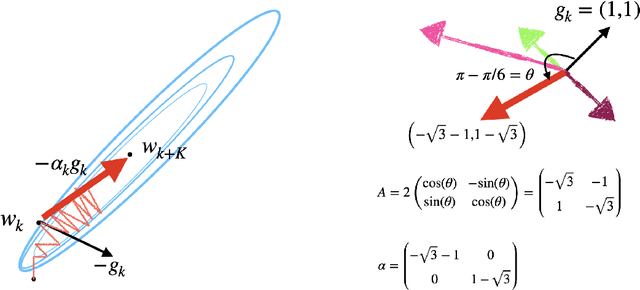
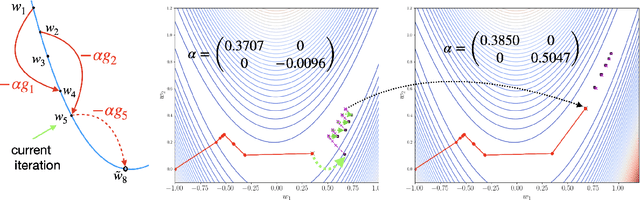
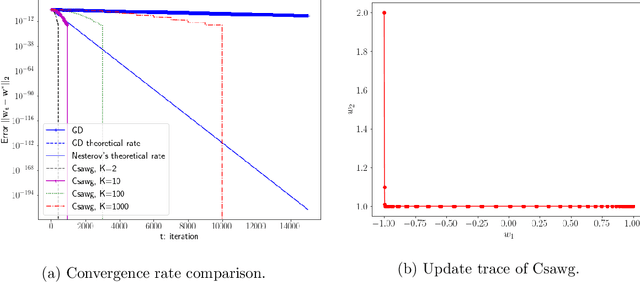
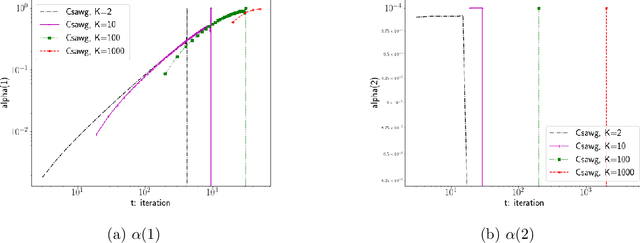
Gradient descent is slow to converge for ill-conditioned problems and non-convex problems. An important technique for acceleration is step-size adaptation. The first part of this paper contains a detailed review of step-size adaptation methods, including Polyak step-size, L4, LossGrad, Adam, IDBD, and Hypergradient descent, and the relation of step-size adaptation to meta-gradient methods. In the second part of this paper, we propose a new class of methods of accelerating gradient descent that have some distinctiveness from existing techniques. The new methods, which we call {\em step-size planning}, use the {\em update experience} to learn an improved way of updating the parameters. The methods organize the experience into $K$ steps away from each other to facilitate planning. From the past experience, our planning algorithm, Csawg, learns a step-size model which is a form of multi-step machine that predicts future updates. We extends Csawg to applying step-size planning multiple steps, which leads to further speedup. We discuss and highlight the projection power of the diagonal-matrix step-size for future large scale applications. We show for a convex problem, our methods can surpass the convergence rate of Nesterov's accelerated gradient, $1 - \sqrt{\mu/L}$, where $\mu, L$ are the strongly convex factor of the loss function $F$ and the Lipschitz constant of $F'$, which is the theoretical limit for the convergence rate of first-order methods. On the well-known non-convex Rosenbrock function, our planning methods achieve zero error below 500 gradient evaluations, while gradient descent takes about 10000 gradient evaluations to reach a $10^{-3}$ accuracy. We discuss the connection of step-size planing to planning in reinforcement learning, in particular, Dyna architectures.

Explainable Artificial Intelligence for Autonomous Driving: A Comprehensive Overview and Field Guide for Future Research Directions

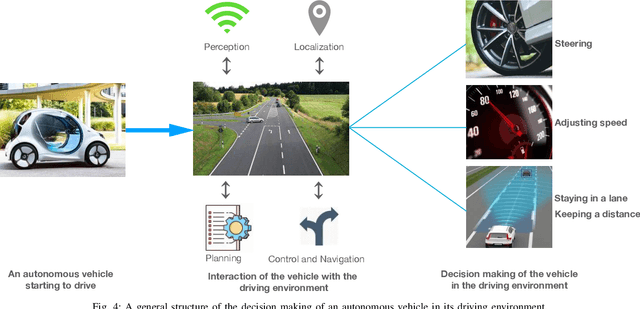
Autonomous driving has achieved a significant milestone in research and development over the last decade. There is increasing interest in the field as the deployment of self-operating vehicles on roads promises safer and more ecologically friendly transportation systems. With the rise of computationally powerful artificial intelligence (AI) techniques, autonomous vehicles can sense their environment with high precision, make safe real-time decisions, and operate more reliably without human interventions. However, intelligent decision-making in autonomous cars is not generally understandable by humans in the current state of the art, and such deficiency hinders this technology from being socially acceptable. Hence, aside from making safe real-time decisions, the AI systems of autonomous vehicles also need to explain how these decisions are constructed in order to be regulatory compliant across many jurisdictions. Our study sheds a comprehensive light on developing explainable artificial intelligence (XAI) approaches for autonomous vehicles. In particular, we make the following contributions. First, we provide a thorough overview of the present gaps with respect to explanations in the state-of-the-art autonomous vehicle industry. We then show the taxonomy of explanations and explanation receivers in this field. Thirdly, we propose a framework for an architecture of end-to-end autonomous driving systems and justify the role of XAI in both debugging and regulating such systems. Finally, as future research directions, we provide a field guide on XAI approaches for autonomous driving that can improve operational safety and transparency towards achieving public approval by regulators, manufacturers, and all engaged stakeholders.

Towards safe, explainable, and regulated autonomous driving

There has been growing interest in the development and deployment of autonomous vehicles on modern road networks over the last few years, encouraged by the empirical successes of powerful artificial intelligence approaches (AI), especially in the applications of deep and reinforcement learning. However, there have been several road accidents with ``autonomous'' cars that prevent this technology from being publicly acceptable at a wider level. As AI is the main driving force behind the intelligent navigation systems of such vehicles, both the stakeholders and transportation jurisdictions require their AI-driven software architecture to be safe, explainable, and regulatory compliant. We present a framework that integrates autonomous control, explainable AI architecture, and regulatory compliance to address this issue and further provide several conceptual models from this perspective, to help guide future research directions.

Exploring the Robustness of Distributional Reinforcement Learning against Noisy State Observations

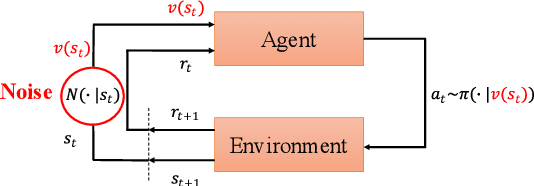
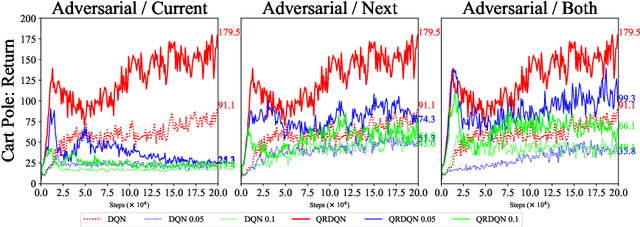
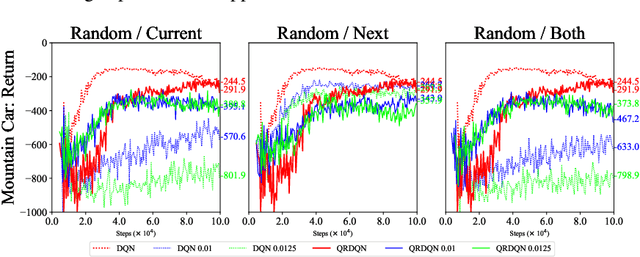
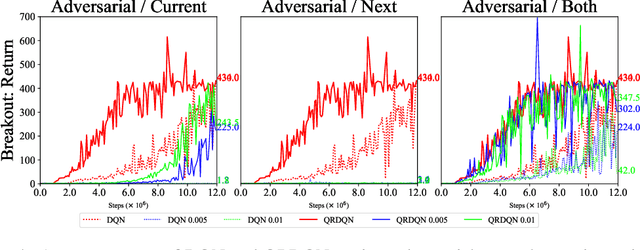
In real scenarios, state observations that an agent observes may contain measurement errors or adversarial noises, misleading the agent to take suboptimal actions or even collapse while training. In this paper, we study the training robustness of distributional Reinforcement Learning~(RL), a class of state-of-the-art methods that estimate the whole distribution, as opposed to only the expectation, of the total return. Firstly, we propose State-Noisy Markov Decision Process~(SN-MDP) in the tabular case to incorporate both random and adversarial state observation noises, in which the contraction of both expectation-based and distributional Bellman operators is derived. Beyond SN-MDP with the function approximation, we theoretically characterize the bounded gradient norm of histogram-based distributional loss, accounting for the better training robustness of distribution RL. We also provide stricter convergence conditions of the Temporal-Difference~(TD) learning under more flexible state noises, as well as the sensitivity analysis by the leverage of influence function. Finally, extensive experiments on the suite of games show that distributional RL enjoys better training robustness compared with its expectation-based counterpart across various state observation noises.