Exploring the Robustness of Distributional Reinforcement Learning against Noisy State Observations

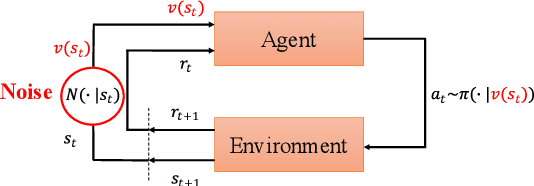
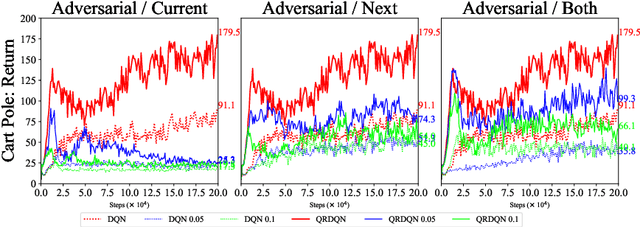
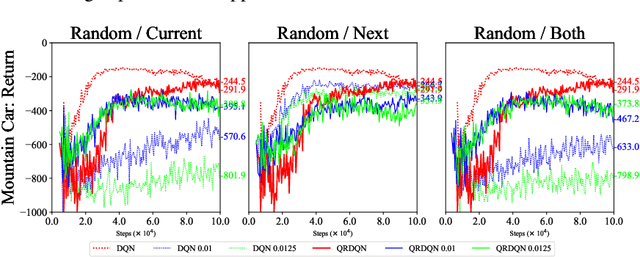
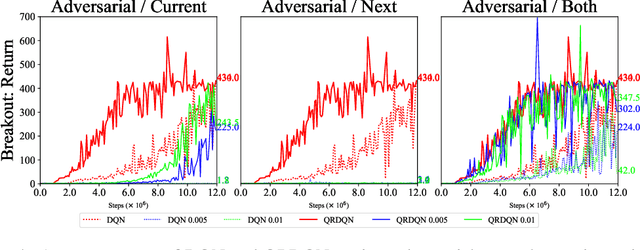
In real scenarios, state observations that an agent observes may contain measurement errors or adversarial noises, misleading the agent to take suboptimal actions or even collapse while training. In this paper, we study the training robustness of distributional Reinforcement Learning~(RL), a class of state-of-the-art methods that estimate the whole distribution, as opposed to only the expectation, of the total return. Firstly, we propose State-Noisy Markov Decision Process~(SN-MDP) in the tabular case to incorporate both random and adversarial state observation noises, in which the contraction of both expectation-based and distributional Bellman operators is derived. Beyond SN-MDP with the function approximation, we theoretically characterize the bounded gradient norm of histogram-based distributional loss, accounting for the better training robustness of distribution RL. We also provide stricter convergence conditions of the Temporal-Difference~(TD) learning under more flexible state noises, as well as the sensitivity analysis by the leverage of influence function. Finally, extensive experiments on the suite of games show that distributional RL enjoys better training robustness compared with its expectation-based counterpart across various state observation noises.